2016-2017学年江苏省苏州市张家港二中八年级上学期期中数学试卷

试卷更新日期：2017-02-15 类型：期中考试

进入出卷网下载

一、选择题

1. 下列平面图形中，不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 如图，已知∠1=∠2，则不一定能使△ABD≌△ACD的条件是（）

A、AB=AC B、BD=CD C、∠B=∠C D、∠BDA=∠CDA

查看试题解析
3. 如果一个数的平方根等于它的立方根，则这个数是（）

A、0 B、1 C、﹣1 D、±1

查看试题解析
4. 下列各式中，正确的是（）

A、 $\sqrt{16}$ =±4 B、± $\sqrt{16}$ =4 C、 $\sqrt[3]{- 27}$ =﹣3 D、 $\sqrt{{(- 4)}^{2}}$ =﹣4

查看试题解析
5. 在﹣2， $\sqrt{4}$ ， $\frac{\sqrt{2}}{2}$ ，3.14， $\frac{22}{3}$ ，（ $\sqrt{2}$ ）⁰中有理数的个数是（）

A、5 B、4 C、3 D、2

查看试题解析
6. 下列四组线段中，可以构成直角三角形的是（）

A、5，6，7 B、0.7，2.4，2.5 C、1，1，2 D、1， $\sqrt{2}$ ，3

查看试题解析
7. 到三角形三边的距离相等的点P应是三角形的三条（）的交点．

A、角平分线 B、高 C、中线 D、垂直平分线

查看试题解析
8. 直角三角形两直角边长分别为3和4，则它斜边上的高是（）

A、3.5 B、2.4 C、1.2 D、5

查看试题解析
9. 如图，在△ABC中，AO⊥BC，垂足为O，若AO=4，∠B=45°，△ABC的面积为10，则AC边长的平方的值是（）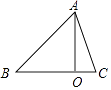

A、16 B、17 C、6 D、18

查看试题解析
10. 如图，在△ABC中，∠ACB=90°，以AC为一边在△ABC外侧作等边三角形ACD，过点D作DE⊥AC，垂足为F，DE与AB相交于点E，连接CE，AB=15cm，BC=9cm，P是射线DE上的一点．连接PC、PB，若△PBC的周长最小，则最小值为（）

A、22cm B、21cm C、24 cm D、27cm

查看试题解析

二、填空题

11. 若等腰三角形的边长分别为2和6，则它的周长为

查看试题解析
12. 如图，已知Rt△ABC中，∠ACB=90°，D是AB的中点，AB=5，则CD= ．

查看试题解析
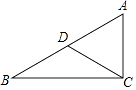13. 如图，在△ABC中，AB=AD=DC，∠BAD=20°，则∠C= ．

查看试题解析
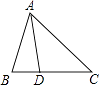14. 如图，以Rt△ABC的三边向外作正方形，若最大正方形的边长为7cm，以AC为边的正方形的面积为25cm² ，则正方形M的面积为 cm² ．

查看试题解析
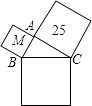15. 如图，在△ABC中，DE是AC的垂直平分线，AE=5cm，△ABC的周长为26cm，则△ABD的周长为 cm．

查看试题解析
16. 如图，在Rt△ABC中，∠ACB=90°，AD平分∠BAC与BC相交于点D，若BD=5，CD=3，则AB的长是．

查看试题解析
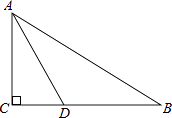17. 如图，在△ABC中，AB=AC=10厘米，BC=8厘米，点D为AB的中点，如果点P在线段BC上以3厘米/秒的速度由B点向C点运动，同时点Q在线段CA上由C点向A点运动，当一个点停止运动时，另一个点也随之停止运动，当点Q的运动速度为时，能够在某一时刻使△BPD与△CQP全等．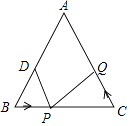

查看试题解析

三、解答题

18. 求下列各式的值：

(1)、求y的值：（2y﹣3）²﹣64=0；

(2)、求x的值：64（x+1）³﹣125=0．

查看试题解析
19. 计算：

(1)、（ $\sqrt{4}$ ）²﹣ $\sqrt[3]{- 27}$ ﹣ $\sqrt{6^{2} + 8^{2}}$

(2)、﹣ $\frac{1}{2^{2}}$ + $\sqrt{2^{2}}$ ﹣ $\sqrt[3]{8}$ +（ $\frac{π}{3}$ ）⁰﹣|﹣1+ $\frac{1}{4}$ |．

查看试题解析
20. 解答题。

(1)、已知（x﹣1）的平方根是±3，（x﹣2y+1）的立方根是3，求x²﹣y²的平方根．

(2)、已知y= $\sqrt{x - 24}$ + $\sqrt{24 - x}$ ﹣8，求 $\sqrt[3]{x - 5 y}$ 的值．

查看试题解析
21. 尺规作图：如左图，在四边形ABCD内找一点P，使得点P到AB、AD的距离相等，并且点P到点B、C的距离也相等．（不写作法，保留作图痕迹）．

查看试题解析
22. 如图，△ABC中，AB=AC，∠A=36°，AC的垂直平分线交AB于E，D为垂足，连接EC．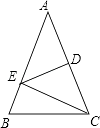

(1)、求∠ECD的度数；

(2)、若CE=5，求BC长．

查看试题解析
23. 如图，在三角形纸片ABC中，∠C=90°，AC=6，折叠该纸片使点C落在AB边上的D点处，折痕BE与AC交于点E．若AD=BD，求折痕BE的长．

查看试题解析
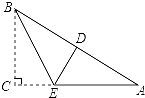24. 已知：如图，在四边形ABCD中，∠ABC=∠ADC=90°，点E是AC的中点，连接BE、BD、DE．

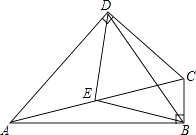(1)、求证：△BED是等腰三角形；

(2)、当∠BAD=°时，△BED是等腰直角三角形．

查看试题解析
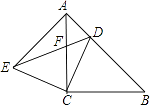
25. 已知：如图，△ABC和△ECD都是等腰直角三角形，∠ACB=∠DCE=90°，D为AB边上的一点，
求证：△ACE≌△BCD．

查看试题解析
26. 角平分线上的点到角两边的距离相等．这一性质在解决图形面积问题时有何妙用呢？阅读材料：已知，如图（1），在面积为S的△ABC中，BC=a，AC=b，AB=c，三条角平分线的交点O到三边的距离为r．连接OA、OB、OC，△ABC被划分为三个小三角形．
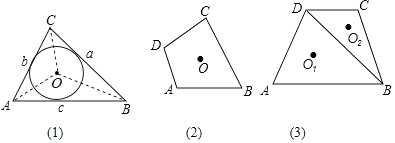∵S=S_△_OBC+S_△_OAC+S_△_OAB= $\frac{1}{2}$ BC•r+ $\frac{1}{2}$ AC•r+ $\frac{1}{2}$ AB•r= $\frac{1}{2}$ （a+b+c）•r，∴r= $\frac{2 S}{a + b + c}$

(1)、类比推理：若面积为S的四边形ABCD的四条角平分线交于O点，如图（2），各边长分别为AB=a，BC=b，CD=c，AD=d，求点O到四边的距离r；

(2)、理解应用：如图（3），在四边形ABCD中，AB∥DC，AB=21，CD=11，AD=BC=13，对角线BD=20，点O₁与O₂分别为△ABD与△BCD的三条角平分线的交点，设它们到各自三角形三边的距离为r₁和r₂ ，求 $\frac{r_{1}}{r_{2}}$ 的值．

查看试题解析
27.
如图，长方形ABCD中，AB=4cm，BC=6cm，现有一动点P从A出发以2cm/秒的速度，沿矩形的边A﹣B﹣C运动，设点P运动的时间为t秒．

(1)、当t为何值时，点P与点A的距离为5cm？

(2)、当t为何值时，△APD是等腰三角形？

(3)、当t为何值时，（2＜t＜5），以线段AD、CP、AP的长度为三边长的三角形是直角三角形，且AP是斜边？

查看试题解析