2017高考数学备考复习（文科）专题十二：统计案例

试卷更新日期：2017-02-15 类型：一轮复习

进入出卷网下载

一、单选题

1. 对变量 $y$ 与 $x$ ，分别选择了4个不同的回归方程甲、乙、丙、丁，它们的相关系数 $r$ 分别为： $r_{1} = - 0.75$ ， $r_{2} = - 0.80$ ， $r_{3} = - 0.5$ ， $r_{4} = - 0.25$ . 其中拟合效果最好的是方程（）.

A、甲 B、乙 C、丙 D、丁

查看试题解析
2. 工人月工资y（元）与劳动生产率x（千元）变化的回归方程 $\bar{y} = 50 + 80 \bar{x}$ ，下列判断正确的是 ( )　
①劳动生产率为1千元时，工资约为130元　
②劳动生产率提高1千元时，月工资约提高80元　
③劳动生产率提高1千元时，月工资约提高130元　
④当月工资为210元时，劳动生产率约为2千元　

A、① ②　 B、① ② ④　 C、② ④　 D、① ② ③ ④

查看试题解析
3. 已知变量 $x$ 和 $y$ 满足关系 $y = - 0.1 x + 1$ ，变量 $y$ 与 $z$ 正相关. 下列结论中正确的是（）

A、 $x$ 与 $y$ 负相关， $x$ 与 $z$ 负相关 B、 $x$ 与 $y$ 正相关， $x$ 与 $z$ 正相关 C、 $x$ 与 $y$ 正相关， $x$ 与 $z$ 负相关 D、 $x$ 与 $y$ 负相关， $x$ 与 $z$ 正相关

查看试题解析
4. 下表是一位母亲给儿子作的成长记录：
年龄/周岁
3
4
5
6
7
8
9
身高/cm
94.8
104.2
108.7
117.8
124.3
130.8
139.1
根据以上样本数据，她建立了身高 y （cm）与年龄x（周岁）的线性回归方程为 $\overset{\land}{y}$ =7.19x+73.93，给出下列结论：
①y与x具有正的线性相关关系；
②回归直线过样本的中心点（42，117.1）；
③儿子10岁时的身高是145.83 cm；
④儿子年龄增加1周岁，身高约增加 7.19 cm.
其中，正确结论的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
5.
某高校《统计》课程的教师随机给出了选该课程的一些情况，具体数据如下：

非统计专业
统计专业
男
13
10
女
7
20
为了判断选修统计专业是否与性别有关，根据表中数据，得，因为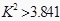，所以可以判定选修统计专业与性别有关.那么这种判断出错的可能性为（）

A、5% B、95% C、1% D、99%

查看试题解析
6. 为了考察两个变量x和y之间的线性相关性，甲、乙两同学各自独立地做100次和150次试验，并且利用线性回归方法，求得回归直线分别为t₁和t₂ ，已知两个人在试验中发现对变量x的观测值的平均值都是s，对变量y的观测值的平均值都是t，那么下列说法正确的是（　　）

A、t₁和t₂有交点（s，t） B、t₁和t₂相交，但交点不是（s，t） C、t₁和t₂必定重合 D、t₁和t₂必定不重合

查看试题解析
7.
如图所示，样本A和B分别取自两个不同的总体，它们的样本平均数分别为 $\bar{X_{A}}$ 、 $\bar{X_{B}}$ ，样本标准差分别为S_A ， S_B ，则（）

A、 $\bar{X_{A}}$ ＞ $\bar{X_{B}}$ ，S_A＞S_B B、 $\bar{X_{A}}$ ＜ $\bar{X_{B}}$ ，S_A＞S_B C、 $\bar{X_{A}}$ ＞ $\bar{X_{B}}$ ，S_A＜S_B D、 $\bar{X_{A}}$ ＜ $\bar{X_{B}}$ ，S_A＜S_B

查看试题解析
8. 已知具有线性相关关系的两个变量x，y之间的一组数据如表：
x
0
1
2
3
4
y
2.2
4.3
4.5
4.8
6.7
且回归直线方程为 $\hat{y}$ =bx+2.6，根据模型预报当x=6时，y的预测值为（）

A、5.76 B、6.8 C、8.3 D、8.46

查看试题解析
9. 有线性相关关系的两个变量x与y有如表对应关系，则其线性回归直线必过点（）
x
2
3
4
5
6
y
2.2
3.8
5.5
6.5
7.0

A、（4，5.5） B、（4，5） C、（5，5） D、（6，7）

查看试题解析
10. 有一位同学家开了一个小卖部，他为了研究气温对热饮销售的影响，经过统计得到了一天所卖的热饮杯数（y）与当天气温（x℃）之间的线性关系，其回归方程为 $\hat{y}$ =﹣2.35x+147.77．如果某天气温为2℃时，则该小卖部大约能卖出热饮的杯数是（）

A、140 B、143 C、152 D、156

查看试题解析
11. 通过随机询问11名性别不同的大学生是否爱好某项运动，得到如下的列联表：
男
女
总计
爱好
40
20
60
不爱好
20
30
50
总计
60
50
110
参照附表，得到的正确结论是（）

A、有99%以上的把握认为“爱好该项运动与性别有关” B、有99%以上的把握认为“爱好该项运动与性别无关” C、在犯错误的概率不超过0.1%的前提下，认为“爱好该项运动与性别有关” D、在犯错误的概率不超过0.1%的前提下，认为“爱好该项运动与性别无关”

查看试题解析
12. 某商场为了了解毛衣的月销售量y（件）与月平均气温x（℃）之间的关系，随机统计了某4个月的月销售量与当月平均气温，其数据如下表：
月平均气温x（℃）
17
13
8
2
月销售量y（件）
24
33
40
55
由表中数据算出线性回归方程 $\hat{y}$ =bx+a中的b=﹣2，气象部门预测下个月的平均气温约为6℃，据此估计该商场下个月毛衣销售量约为（）件．

A、46 B、40 C、38 D、58

查看试题解析
13. 在2013年9月15日，某市物价部门对本市的5家商场的某种商品的一天销售量及其价格进行调查，5家商场的售价x元和销售量y件之间的一组数据如下表所示：
价格x
9
9.5
10
10.5
11
销售量y
11
10
8
6
5
由散点图可知，销售量y与价格x之间有较好的线性相关关系，其线性回归方程是：y=﹣3.2x+a，则a=（）

A、﹣24 B、35.6 C、40.5 D、40

查看试题解析
14. 通过随机询问110名性别不同的大学生是否爱好某项运动，得到如下的列联表：
男
女
合    计
爱好
40
20
60
不爱好
20
30
50
合    计
60
50
110
根据上述数据能得出的结论是（   ）
（参考公式与数据：X²= $\frac{n {(n_{11} n_{22} - n_{12} n_{21})}^{2}}{n_{1} + n_{2} + n_{1} + n_{2}}$ ．当X²＞3.841时，有95%的把握说事件A与B有关；当X²＞6.635时，有99%的把握说事件A与B有关；当X²＜3.841时认为事件A与B无关．）

A、有99%的把握认为“爱好该项运动与性别有关” B、有99%的把握认为“爱好该项运动与性别无关” C、在犯错误的概率不超过0.1%的前提下，认为“爱好该项运动与性别有关” D、在犯错误的概率不超过0.1%的前提下，认为“爱好该项运动与性别无关”．

查看试题解析
15. 下列四个图各反映了两个变量的某种关系，其中可以看作具有较强线性相关关系的是（）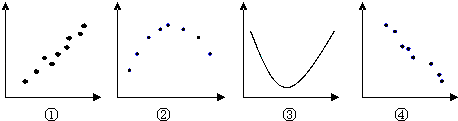

A、①③ B、①④ C、②③ D、①②

查看试题解析

二、填空题

16. 为考察高中生的性别与是否喜欢数学课程之间的关系，在我市某普通中学高中生中随机抽取200名学生，得到如下2×2列联表：

喜欢数学课
不喜欢数学课
合计
男
30
60
90
女
20
90
110
合计
50
150
200
经计算K²≈6.06，根据独立性检验的基本思想，约有（填百分数）的把握认为“性别与喜欢数学课之间有关系”.

查看试题解析
17. 为了调查患慢性气管炎是否与吸烟有关，调查了339名50岁以上的人，调查结果如下表

患慢性气管炎
未患慢性气管炎
合计
吸烟
43
162
205
不吸烟
13
121
134
合计
56
283
339
根据列联表数据，求得K² = .

查看试题解析
18. 某同学在求解某回归方程中，已知x，y的取值结果（y与x呈线性相关）如表：
x
2
3
4
y
6
4
m
并且求得了线性回归方程为 $\hat{y}$ =﹣ $\frac{1}{2}$ x+ $\frac{13}{2}$ ，则m等于．

查看试题解析
19. 某地区2007年至2013年农村居民家庭人均纯收入y（单位：千元）的统计数据如表，
年份
2007
2008
2009
2010
2011
2012
2013
年份代号x
1
2
3
4
5
6
7
y
2.9
3.3
3.6
4.4
4.8
5.2
5.9
据此，我们得到y关于年份代号x的线性回归方程： $\hat{y}$ =0.5 $\hat{x}$ +2.3，则预测该地区2015年农村居民家庭人均纯收入等于．

查看试题解析
20. 已知x、y的取值如表所示：
x
0
1
3
4
y
2.2
4.3
4.8
6.7
从散点图分析，y与x线性相关，且 $\hat{y}$ =0.95x+a，则a= ．

查看试题解析

三、综合题

21. 某种产品的广告费用支出x万元与销售额y万元之间有如下的对应数据：
x
2
4
5
6
8
y
30
40
60
50
70

(1)、画出散点图；

(2)、求回归直线方程；

(3)、据此估计广告费用为12万元时，销售收入y的值．

查看试题解析
22. 某种产品的广告费支出x与销售额y（单位：万元）之间有如下对应数据：
x
2
4
5
6
8
y
30
40
60
50
70

(1)、求回归直线方程；

(2)、试预测广告费支出为10万元时，销售额多大？

(3)、在已有的五组数据中任意抽取两组，求至少有一组数据其预测值与实际值之差的绝对值不超过5的概率．

查看试题解析
23. 某种产品的广告费支出x与销售额y（单位：百万元）之间有如下对应：
X
2
4
5
6
8
y
30
40
60
50
70

(1)、求回归直线方程．

(2)、回归直线必经过的一点是哪一点？

查看试题解析
24. “女大学生就业难”究竟有多难？其难在何处？女生在求职中是否收到了不公平对待？通过对某大学应届毕业生的调查与实证分析试对下列问题提出解答．为调查某地区大学应届毕业生的调查，用简单随机抽样方法从该地区抽取了500为大学生做问卷调查，结果如下：
性别
是否公平
男
女
公平
40
30
不公平
160
270

(1)、估计该地区大学生中，求职中收到了公平对待的学生的概率；

(2)、能否有99%的把握认为该地区的大学生求职中受到了不公平对待与性别有关？

(3)、根据（2）的结论，能否提出更好的调查方法来估计该地区的大学生中，求职中是否受到了不公平对待学生的比例？说明理由．
附：K²= $\frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}$
P（K²≥k）
0.000
0.010
0.001
k
3.841
6.635
10.828

查看试题解析
25. 某成衣批发店为了对一款成衣进行合理定价，将该款成衣按事先拟定的价格进行试销，得到了如下数据：
批发单价x（元）
80
82
84
86
88
90
销售量y（件）
90
84
83
80
75
68

(1)、求回归直线方程 $\hat{y} = \hat{b} x + \hat{a}$ ，其中 $\hat{b} = - 2$

(2)、预测批发单价定为85元时，销售量大概是多少件？

(3)、假设在今后的销售中，销售量与批发单价仍然服从（1）中的关系，且该款成衣的成本价为40元/件，为使该成衣批发店在该款成衣上获得更大利润，该款成衣单价大约定为多少元？

查看试题解析

年龄/周岁	3	4	5	6	7	8	9
身高/cm	94.8	104.2	108.7	117.8	124.3	130.8	139.1

月平均气温x（℃）	17	13	8	2
月销售量y（件）	24	33	40	55

	喜欢数学课	不喜欢数学课	合计
男	30	60	90
女	20	90	110
合计	50	150	200

	患慢性气管炎	未患慢性气管炎	合计
吸烟	43	162	205
不吸烟	13	121	134
合计	56	283	339

年份	2007	2008	2009	2010	2011	2012	2013
年份代号x	1	2	3	4	5	6	7
y	2.9	3.3	3.6	4.4	4.8	5.2	5.9

批发单价x（元）	80	82	84	86	88	90
销售量y（件）	90	84	83	80	75	68

	非统计专业	统计专业
男	13	10
女	7	20

x	0	1	2	3	4
y	2.2	4.3	4.5	4.8	6.7

x	2	3	4	5	6
y	2.2	3.8	5.5	6.5	7.0

	男	女	总计
爱好	40	20	60
不爱好	20	30	50
总计	60	50	110