2016-2017学年江苏省苏州市昆山市、太仓市八年级上学期期中数学试卷

试卷更新日期：2017-02-15 类型：期中考试

进入出卷网下载

一、选择题

1. 下面有4个汽车标志图案，其中是轴对称图形的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 下列说法正确的是（）

A、9的立方根是3 B、算术平方根等于它本身的数一定是1 C、﹣2是4的平方根 D、 $\sqrt{16}$ 的算术平方根是4

查看试题解析
3. 下列说法正确的是（　　）

A、全等三角形是指形状相同的两个三角形 B、全等三角形的周长和面积分别相等 C、全等三角形是指面积相等的两个三角形 D、所有的等边三角形都是全等三角形

查看试题解析
4. 如图，∠CAB=∠DBA，再添加一个条件，不一定能判定△ABC≌△BAD的是（）

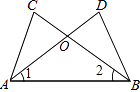A、AC=BD B、∠1=∠2 C、AD=BC D、∠C=∠D

查看试题解析
5. 在 $\sqrt{16}$ ，﹣3.14， $\frac{π}{2}$ ，﹣0.3， $\sqrt{2}$ ，0.5858858885…， $\frac{22}{7}$ 中无理数有（）

A、3个 B、4个 C、5个 D、6个

查看试题解析
6. 如果点P（﹣2，b）和点Q（a，﹣3）关于x轴对称，则a+b的值是（）

A、﹣1 B、1 C、﹣5 D、5

查看试题解析
7. 如图，已知等边△ABC中，BD=CE，AD与BE相交于点P，则∠APE的度数为（）

A、45° B、60° C、55° D、75°

查看试题解析
8. 已知等腰三角形的两边长分別为a、b，且a、b满足 $\sqrt{2 a - 3 b + 5}$ +（2a+3b﹣13）²=0，则此等腰三角形的周长为（）

A、7或8 B、6或10 C、6或7 D、7或10

查看试题解析
9. 如图，AD是△ABC的角平分线，DF⊥AB，垂足为F，DE=DG，△ADG和△AED的面积分别为50和39，则△EDF的面积为（）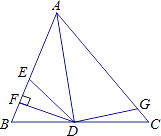

A、11 B、5.5 C、7 D、3.5

查看试题解析
10. 已知：如图，BD为△ABC的角平分线，且BD=BC，E为BD延长线上的一点，BE=BA，过E作EF⊥AB，F为垂足．下列结论：①△ABD≌△EBC；②∠BCE+∠BCD=180°；③AD=AE=EC；④BA+BC=2BF．其中正确的是（）

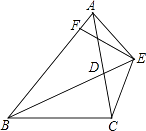A、①②③ B、①③④ C、①②④ D、①②③④

查看试题解析

二、填空题

11. $\sqrt{16}$ 的平方根是．

查看试题解析
12. 如图，OC是∠AOB的平分线，PD⊥DA，垂足为D，PD=2，则点P到OB的距离是．

查看试题解析
13. 如图，a∥b，点A在直线a上，点C在直线b上，∠BAC=90°，AB=AC，若∠1=20°，则∠2的度数为．

查看试题解析
14. 已知 $\sqrt{a - 2}$ + $\sqrt{b + 3}$ =0，那么（a+b）²⁰¹⁶的值为．

查看试题解析
15. 若一个正数的两个不同的平方根为2m﹣6和m+3，则m为

查看试题解析
16. 若等腰三角形的一个外角是80°，则等腰三角形的底角是°．

查看试题解析
17. 如图，在2×2的正方形格纸中，有一个以格点为顶点的△ABC，请你找出格纸中所有与△ABC成轴对称且也以格点为顶点的三角形，这样的三角形共有个．

查看试题解析
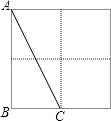18. 如图，等边△ABC中，AB=4，E是线段AC上的任意一点，∠BAC的平分线交BC于D，AD=2 $\sqrt{3}$ ，F是AD上的动点，连接CF、EF，则CF+EF的最小值为．

查看试题解析

三、解答题

19. 计算或化简：

(1)、（ $\sqrt{4}$ ）²﹣ $\sqrt[3]{8}$ ﹣ $\sqrt{3^{2} + 4^{2}}$

(2)、﹣ $\sqrt{3}$ +（1﹣ $\sqrt{2}$ ）⁰﹣| $\sqrt{3}$ ﹣2|

查看试题解析
20. 求下列各式中x的值

(1)、（x+1）²﹣3=0；

(2)、3x³+4=﹣20．

查看试题解析
21. 已知5x﹣1的算术平方根是3，4x+2y+1的立方根是1，求4x﹣2y的平方根．

查看试题解析
22. 已知：如图，AB∥CD，E是AB的中点，CE=DE．求证：

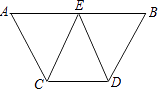(1)、∠AEC=∠BED；

(2)、AC=BD．

查看试题解析
23. 已知：如图，在△ABC、△ADE中，∠BAC=∠DAE=90°，AB=AC，AD=AE，点C、D、E三点在同一直线上，连接BD．
求证：

(1)、△BAD≌△CAE；

(2)、试猜想BD、CE有何特殊位置关系，并证明．

查看试题解析
24. 如图，△ABC中，AD⊥BC，EF垂直平分AC，交AC于点F，交BC于点E，且BD=DE．

(1)、若∠BAE=40°，求∠C的度数；

(2)、若△ABC周长13cm，AC=6cm，求DC长．

查看试题解析
25. 如图，方格纸上画有AB、CD两条线段，按下列要求作图（不保留作图痕迹，不要求写出作法）
请你在图（1）中画出线段AB关于CD所在直线成轴对称的图形；请你在图（2）中添上一条线段，使图中的3条线段组成一个轴对称图形，请画出所有情形．

查看试题解析
26. 在△ABC中，AB边的垂直平分线l₁交BC于D，AC边的垂直平分线l₂交BC于E，l₁与l₂相交于点O．△ADE的周长为6cm．

(1)、求BC的长；

(2)、分别连结OA、OB、OC，若△OBC的周长为16cm，求OA的长．

查看试题解析
27. 已知：在△ABC中，AC=BC，∠ACB=90°，点D是AB的中点，点E是AB边上一点．

(1)、直线BF垂直于直线CE于点F，交CD于点G（如图1），求证：AE=CG；

(2)、直线AH垂直于直线CE，垂足为点H，交CD的延长线于点M（如图2），找出图中与BE相等的线段，并证明．

查看试题解析
28. 问题背景：

(1)、如图1：在四边形ABCD中，AB=AD，∠BAD=120°，∠B=∠ADC=90°．E，F分别是BC，CD上的点．且∠EAF=60°．探究图中线段BE，EF，FD之间的数量关系．小王同学探究此问题的方法是，延长FD到点G．使DG=BE．连结AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出结论，他的结论应是．
探索延伸：

(2)、如图2，若在四边形ABCD中，AB=AD，∠B+∠D=180°．E，F分别是BC，CD上的点，且∠EAF= $\frac{1}{2}$ ∠BAD，上述结论是否仍然成立，并说明理由．

查看试题解析