2016-2017学年河北省秦皇岛市抚宁区台营学区八年级上学期期中数学试卷
试卷更新日期：2017-02-15 类型：期中考试
一、精心选一选，慧眼识金！
-
1. 点M（﹣3，2）关于y轴对称的点的坐标为（ ）A、（﹣3，﹣2） B、（3，﹣2） C、（3，2） D、（﹣3，2）2. 下列各组数中，互为相反数的是 （ ）A、﹣2与 B、﹣2与﹣ C、﹣2与﹣ D、﹣2与3. 如果一个等腰三角形的周长为15cm，一边长为3cm，那么腰长为（ ）A、3cm B、6cm C、5cm D、3cm或6cm4. 请你指出在这几个图案中是轴对称图形的有 （ ）
A、1个 B、2个 C、3个 D、4个5. 数轴上表示1， 的对应点分别为A，B，点B关于点A的对称点为C，则点C所表示的数是（ ）
A、 ﹣1 B、1﹣ C、2﹣ D、 ﹣26. 下列说法中，正确的是（ ）A、两个关于某直线对称的图形是全等图形 B、两个图形全等，它们一定关于某直线对称 C、两个全等三角形对应点连线的垂直平分线就是它们的对称轴 D、两个三角形关于某直线对称，对称点一定在直线两旁7. 如图，AB∥CD，且AB=CD，则△ABE≌△CDE的根据是（ ）
A、只能用ASA B、只能用SAS C、只能用AAS D、用ASA或AAS8. 估计 +3的值（ ）A、在5和6之间 B、在6和7之间 C、在7和8之间 D、在8和9之间9. 如图，△ABC中，∠C=90°，AC=BC，AD平分∠CAB交BC于D，DE⊥AB于E且AB=6cm，则△DEB的周长为（ ）
A、40cm B、6cm C、8cm D、10cm10. 如图所示，将一张正方形纸片对折两次，然后在上面打3个洞，则纸片展开后是（ ）
A、
B、
C、
D、
二、填空题
-
11. 点P（3，1）关于x轴的对称点P′的坐标是 ．12. 在：﹣3，0， ，1四个数中最大的数是13. = ．14. 在△ABC中，AB=AC，∠A=40°，则∠B的度数为°．15. 如图，在△ABC中，AB=AC，AD⊥BC于D，DE⊥AB于E，DF⊥AC于F，若DE=3，则DF= ．
16. 观察下列各式： =2 ， =3 ， =4 ，…请你根据你找到的规律写出第6个等式是 ．17. 如图所示，∠A=∠E，AC⊥BE，AB=EF，BE=18，CF=8，则AC= ．
18. 有一个数值转换器，其原理如图所示．当输入的x值是9时，输出的y值为 ．
19. 如图，在△ABC中，AB=AC，AD是BC边上的高，点E、F是AD的三等分点，若△ABC的面积为12cm2 ， 则图中阴影部分的面积是 cm2 ．
20. 如图，在2×2的正方形格纸中，有一个以格点为顶点的△ABC，请你找出格纸中所有与△ABC成轴对称且也以格点为顶点的三角形，这样的三角形共有个．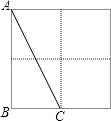
三、解答题
-
21. 解答题。(1)、计算：（ + ）﹣(2)、2x2=8，求x的值．22. 在如图的方格纸中，每个小正方形的边长都为l，△ABC的顶点坐标分别为A（﹣4，4）、B（﹣2，3）、C（﹣3，1）．
(1)、在图中画出与△ABC关于y轴对称的△A1B1C1 ， 并直接写出△A1B1C1的三个顶点坐标；(2)、画出将△A1B1C1向下平移4格得到的△A2B2C2 ， 并直接写出△A2B2C2的三个顶点坐标．23. 已知∠AOB，点M、N，在∠AOB的内部求作一点P．使点P到∠AOB的两边距离相等，且PM=PN（要求：尺规作图，保留作图痕迹，不写作法）．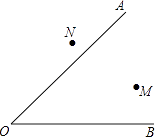
24. 如图，E、F分别为线段AC上的两个点，且DE⊥AC于E，BF⊥AC于F，若AB=CD，AF=CE，BD交AC于点M．求证：MB=MD，ME=MF．
25. 把两块含45°角的直角三角板按图1所示的方式放置，点D在BC上，连结BE、AD，AD的延长线交BE于点F．(1)、如图1，求证：BE=AD，AF⊥BE；(2)、将△ABC绕点C顺时针旋转（如图2），连结BE、AD，AD分别交BE、BC于点F、G，那么（1）中的结论还成立吗？若成立，请证明；若不成立，请说明理由．
26. 在△ABC中，AB=AC．(1)、如图1，如果∠BAD=30°，AD是BC上的高，AD=AE，则∠EDC=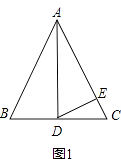
(2)、如图2，如果∠BAD=40°，AD是BC上的高，AD=AE，则∠EDC=
(3)、思考：通过以上两题，你发现∠BAD与∠EDC之间有什么关系？请用式子表示：(4)、如图3，如果AD不是BC上的高，AD=AE，是否仍有上述关系？如有，请你写出来，并说明理由．