2016-2017学年福建省漳州市长泰县八年级上学期期中数学试卷
试卷更新日期：2017-02-15 类型：期中考试
一、选择题
-
1. 16的平方根是（ ）A、±4 B、±2 C、4 D、﹣42. 下列各组数互为相反数的是（ ）A、5和 B、﹣（﹣5）和|﹣5| C、﹣5和 D、﹣5和3. 在实数﹣ ， ，0， ，﹣3.14， 中无理数有（ ）A、2个 B、3个 C、4个 D、5个4. 下列运算式中，正确的是（ ）A、a2•a3=a6 B、（a3）3=a9 C、（2a2）2=2a4 D、a6÷a3=a25. （mx+8）（2﹣3x）展开后不含x的一次项，则m为（ ）A、3 B、0 C、12 D、246. 下列从左边到右边的变形，属于因式分解的是（ ）A、（x+1）（x﹣1）=x2﹣1 B、x2﹣2x+1=x（x﹣2）+1 C、x2﹣4y2=（x﹣2y）2 D、2x2+4x+2=2（x+1）27. 下列各式中，能用平方差公式分解因式的是（ ）A、4x2﹣4x+1 B、﹣a2+b2 C、x2+y2 D、﹣x2﹣y28. 如果整式x2+mx+9恰好是一个整式的平方，那么m的值是（ ）A、±3 B、±4.5 C、±6 D、99. 说明“如果x＜2，那么x2＜4”是假命题，可以举一个反例x的值为（ ）A、﹣1 B、﹣3 C、0 D、1.510. 观察如图，把边长为3的两个正方形沿其对角线长剪开，可得4个直角三角形，这4个直角三角形可拼成一个新的正方形，则新正方形的边长为（ ）
A、3 B、6 C、 D、1811. 如图，在四边形ABCD中，AB=AD，CB=CD，若连接AC、BD相交于点O，则图中全等三角形共有（ ）
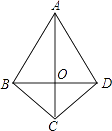A、1对 B、2对 C、3对 D、4对12. 如图，已知AB=AD，那么添加下列一个条件后，仍无法判定△ABC≌△ADC的是（ ）
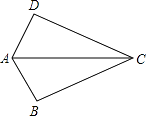A、CB=CD B、∠BAC=∠DAC C、∠BCA=∠DCA D、∠B=∠D=90°二、填空题
-
13. - 的立方根是 ．14. 已知a、b为两个连续整数，且a＜﹣ ＜b，则a+b= ．15. 已知：x满足（x﹣1）2=9，根据平方根的意义可求得x=16. 计算：（5ax2﹣15x）÷（﹣5x）= ．17. 一个长方形的面积是（4x2﹣9）平方米，其长为（2x+3）米，用含x的整式表示它的宽为米．18. 计算：（﹣0.125）2016×82016= ．19. 若2x+3y=4，则4x•8y的值为 ．20. 如果（x+y+1）（x+y﹣1）=63，那么x+y的值为 ．21. 如图，AB、CD相交于点O，AD=CB，请你补充一个条件，使得△AOD≌△COB，你补充的条件是 ．
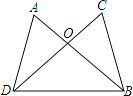
三、解答题
-
22. 分解因式：(1)、ax2﹣16ay2(2)、（x+2）（x﹣6）+16(3)、9a2（x﹣y）+4b2（y﹣x）23. 已知一个正数x的两个平方根分别是3﹣5m和m﹣7，求这个正数x的立方根．24. 解答题。(1)、先化简，再求值：（a+2）2﹣（a+1）（a﹣1），其中a=﹣ ．(2)、已知m﹣n=﹣4，mn=2，求下列代数式的值．
①m2+n2
②（m+1）（n﹣1）
25. 如图，点C，E，F，B在同一直线上，点A，D在BC异侧，AB∥CD，AE=DF，∠A=∠D．求证：AB=CD．
26. 如图，有一块长为a米、宽为b米的长方形空地，现计划在这块空地中间修出两条互相垂直的宽均为2米的道路（图中阴影部分），其余部分进行绿化．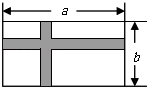
(1)、求出绿地的面积；（用含a、b的代数式表示）(2)、若a=2b，且道路的面积为116米2 ， 求原长方形空地的宽．27. 已知：如图，在△ABC、△ADE中，∠BAC=∠DAE=90°，AB=AC，AD=AE，点C、D、E三点在同一直线上，连接BD．
求证：
(1)、△BAD≌△CAE；(2)、试猜想BD、CE有何特殊位置关系，并证明．28. 阅读材料：分解因式：x2+2x﹣3
解：原式=x2+2x+1﹣4=（x+1）2﹣4
=（x+1+2）（x+1﹣2）=（x+3）（x﹣1）
此种方法抓住了二次项和一次项的特点，然后加一项，使这三项成为完全平方式，我们把这种分解因式的方法叫配方法．请仔细体会配方法的特点，然后尝试用配方法解决下列问题：
(1)、分解因式x2﹣2x﹣3=；a2﹣4ab﹣5b2=；(2)、无论m取何值，代数式m2+6m+13总有一个最小值，请你尝试用配方法求出它的最小值；(3)、观察下面这个形式优美的等式：a2+b2+c2﹣ab﹣bc﹣ca= [（a﹣b）2+（b﹣c）2+（c﹣a）2]该等式从左到右的变形，不仅保持了结构的对称性，还体现了数学的和谐、简洁美．
请你说明这个等式的正确性．