2017高考数学备考复习（文科）专题八：立体几何

试卷更新日期：2017-02-15 类型：一轮复习

进入出卷网下载

一、单选题

1. 设四棱锥P-ABCD的底面不是平行四边形，用平面 $α$ 去截此四棱锥，使得截面是平行四边形，则这样的平面 $α$ （）

A、不存在 B、有且只有1个 C、恰好有4个 D、有无数多个

查看试题解析
2. 已知m，n是两条不同的直线， $α ， β$ 是两个不同的平面，则下列四个命题中是真命题的是(　　　　)

A、 $m \subset α$ ， $m ∥ n$ ，则 $n ∥ α$ B、 $m \subset α$ ， $m ⊥ β$ ，则 $α ⊥ β$ C、 $m \subset α$ ， $n \subset β$ ， $m ∥ n$ ，则 $α ∥ β$ D、 $m \subset α$ ， $n \subset β$ ， $m ⊥ n$ ，则 $α ⊥ β$

查看试题解析
3.
下列四个正方体图形中， $A ， B$ 为正方体的两个顶点， $M ， N ， P$ 分别为其所在棱的中点，能得出 $A B ∥$ 平面 $M N P$ 的图形的序号是(　　)

A、①③ B、①④ C、②③ D、②④

查看试题解析
4. 设α，β，γ为两两不重合的平面，l，m，n为两两不重合的直线，给出下列四个命题：
（1）若α⊥γ，β⊥γ，则α//β；
（2）若m $\subset$ α，n $\subset$ α， $m / / β ， n / / β$ ，则α//β；
（3）若α//β，l $\subset$ α，则l//β；
（4）若 $α \cap β = l ， β \cap γ = m ， γ \cap α = n$ ， l//γ，则m//n．
其中正确的命题是（）

A、（1）（3） B、（2）（3） C、（2）（4） D、（3）（4）

查看试题解析
5. 已知m，n是两条不同直线， $α$ ， $β$ 是两个不同平面，则下列命题正确的是

A、若 $α$ ， $β$ 垂直于同一平面，则 $α$ 与 $β$ 平行 B、若m，n平行于同一平面，则m与n平行 C、若 $α$ ， $β$ 不平行，则在 $α$ 内不存在与 $β$ 平行的直线 D、若m，n不平行，则m与n不可能垂直于同一平面

查看试题解析
6. 设 $α$ ， $β$ 是两个不同的平面，l，m是两条不同的直线，且l $\subset$ $α$ ， m $\subset$ $β$ （）

A、若l $⊥$ $β$ ，则 $α$ $⊥$ $β$ B、若 $α$ $⊥$ $β$ ，则l $⊥$ m C、若l// $β$ ，则 $α$ // $β$ D、若 $α$ // $β$ ，则l//m

查看试题解析
7. 已知直线m∥平面α，则下列命题中正确的是（）

A、α内所有直线都与直线m异面 B、α内所有直线都与直线m平行 C、α内有且只有一条直线与直线m平行 D、α内有无数条直线与直线m垂直

查看试题解析
8.
某工作的三视图如图所示，现将该工作通过切削，加工成一个体积尽可能大的正方体新工件，并使新工件的一个面落在原工作的一个面内，则原工件材料的利用率为（）（材料利用率=新工件的体积/原工件的体积）

A、 $\frac{8}{9π}$ B、 $\frac{8}{27 π}$ C、 $\frac{24 (\sqrt{2} - 1)^{2}}{π}$ D、 $\frac{8 (\sqrt{2} - 1)^{2}}{π}$

查看试题解析
9.
一个几何体的三视图如图所示，则该几何体的表面积为（）

A、3 $π$ B、4 $π$ C、2 $π$ +4 D、3 $π$ +4

查看试题解析
10.
PA垂直于正方形ABCD所在平面，连接PB，PC，PD，AC，BD，则下列垂直关系正确的是（　　）
①面PAB⊥面PBC
②面PAB⊥面PAD
③面PAB⊥面PCD
④面PAB⊥面PAC．

A、①② B、①③ C、②③ D、②④

查看试题解析
11. 下列命题中正确的是（　　）

A、如果两条直线都平行于同一个平面，那么这两条直线互相平行 B、过已知平面的一条斜线有且只有一个平面与已知平面垂直 C、平面a不垂直平面β，但平面α内存在直线垂直于平面β D、若直线l不垂直于平面α，则在平面α内不存在与l垂直的直线

查看试题解析
12. 平面α过正方体ABCD﹣A₁B₁C₁D₁的顶点A，α∥平面CB₁D₁ ， α∩平面ABCD=m，α∩平面ABA₁B₁=n，则m、n所成角的正弦值为（　　）

A、 $\frac{\sqrt{3}}{2}$ B、 $\frac{\sqrt{2}}{2}$ C、 $\frac{\sqrt{3}}{3}$ D、 $\frac{1}{3}$

查看试题解析
13. 已知互相垂直的平面α，β交于直线l，若直线m，n满足m∥α，n⊥β，则（　　）

A、m∥l B、m∥n C、n⊥l D、m⊥n

查看试题解析
14. 已知m，n是两条不同直线，α，β，γ是三个不同平面，下列命题中正确的是（　　）

A、若m∥α，n∥α，则m∥n B、若α⊥γ，β⊥γ，则α∥β C、若m∥α，m∥β，则α∥β D、若m⊥α，n⊥α，则m∥n

查看试题解析
15. 如图，四边形ABCD中，AB=AD=CD=1，BD= $\sqrt{2}$ ，BD⊥CD．将四边形ABCD沿对角线BD折成四面体A′﹣BCD，使平面A′BD⊥平面BCD，则下列结论正确的是（）

A、A′C⊥BD B、∠BA′C=90° C、CA′与平面A′BD所成的角为30° D、四面体A′﹣BCD的体积为 $\frac{1}{3}$

查看试题解析

二、填空题

16.
如图，在直四棱柱A₁B₁C₁D₁﹣ABCD中，当底面四边形ABCD满足条件时，有A₁C⊥B₁D₁ ．（注：填上你认为正确的一种条件即可，不必考虑所有可能的情形．）

查看试题解析
17.
一个四棱锥的三视图如图所示，其左视图是等边三角形，该四棱锥的体积V=

查看试题解析
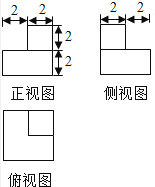
18.
某几何体的三视图如图所示（单位：cm），则该几何体的表面积是cm² ，体积是cm³ ．

查看试题解析
19. α、β是两个平面，m、n是两条直线，有下列四个命题：
①如果m⊥n ， m⊥α ， n∥β ，那么α⊥β.
②如果m⊥α ， n∥α ，那么m⊥n.
③如果α∥β ， m $\subset$ α ，那么m∥β.
④如果m∥n ， α∥β ，那么m与α所成的角和n与β所成的角相等.
其中正确的命题有.(填写所有正确命题的编号）

查看试题解析
20.
如图所示，空间四边形ABCD中，AB=CD，AB⊥CD，E、F分别为BC、AD的中点，则EF和AB所成的角为

查看试题解析

三、解答题

21.
在如图所示的几何体中，AE⊥平面ABC，CD∥AE，F是BE的中点，AC=BC=1，∠ACB=90°，AE=2CD=2．
证明DF⊥平面ABE；

查看试题解析
22.
如图，在三棱锥P﹣ABC中，△ABC是边长为2的正三角形，∠PCA=90°，E，H分别为AP，AC的中点，AP=4，BE= $\sqrt{3}$ ．

（Ⅰ）求证：AC⊥平面BEH；

（Ⅱ）求直线PA与平面ABC所成角的正弦值．

查看试题解析

四、综合题

23.
如图，在四棱锥P﹣ABCD中，PC⊥平面ABCD，AB∥DC，DC⊥AC．

(1)、求证：DC⊥平面PAC；

(2)、求证：平面PAB⊥平面PAC；

(3)、设点E为AB的中点，在棱PB上是否存在点F，使得PA∥平面CEF？说明理由．

查看试题解析
24.
如图，在三棱台ABC﹣DEF中，平面BCFE⊥平面ABC，∠ACB=90°，BE=EF=FC=1，BC=2，AC=3．

(1)、求证：BF⊥平面ACFD；

(2)、求直线BD与平面ACFD所成角的余弦值．

查看试题解析
25.
在如图所示的几何体中，D是AC的中点，EF∥DB．

(1)、已知AB=BC，AE=EC，求证：AC⊥FB；

(2)、已知G，H分别是EC和FB的中点，求证：GH∥平面ABC．

查看试题解析