2017高考数学备考复习(文科)专题三:函数的图象、函数的应用
试卷更新日期:2017-02-15 类型:一轮复习
一、单选题
-
1. 某辆汽车每次加油都把油箱加满,下表记录了该车相邻两次加油时的情况.
加油时间
加油量(升)
加油时的累计里程(千米)
2015年5月1日
12
35000
2015年5月15日
48
35600
注:“累计里程“指汽车从出厂开始累计行驶的路程
在这段时间内,该车每100千米平均耗油量为( )
A、6升 B、8升 C、10升 D、12升2. 已知a为函数f(x)=x3﹣12x的极小值点,则a=( )
A、﹣4 B、﹣2 C、4 D、23. 若函数f(x)=x﹣ sin2x+asinx在(﹣∞,+∞)单调递增,则a的取值范围是( )A、[﹣1,1] B、[﹣1, ] C、[﹣ , ] D、[﹣1,﹣ ]4. 已知函数f(x)的定义域为R.当x<0时,f(x)=x3﹣1;当﹣1≤x≤1时,f(﹣x)=﹣f(x);当x> 时,f(x+ )=f(x﹣ ).则f(6)=( )
A、﹣2 B、﹣1 C、0 D、25. 若函数y=f(x)的图象上存在两点,使得函数的图象在这两点处的切线互相垂直,则称y=f(x)具有T性质.下列函数中具有T性质的是( )A、y=sinx B、y=lnx C、y=ex D、y=x36. 若函数y=logax(a>0,且a≠1)的图象如图所示,则下列函数图象正确的是( )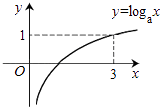 A、
A、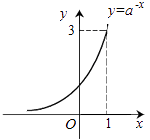 B、
B、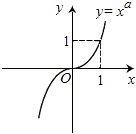 C、
C、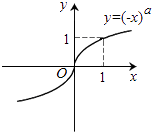 D、
D、 7. 如图,某飞行器在4千米高空飞行,从距着陆点A的水平距离10千米处开始下降,已知下降飞行轨迹为某三次函数图象的一部分,则该函数的解析式为( )
7. 如图,某飞行器在4千米高空飞行,从距着陆点A的水平距离10千米处开始下降,已知下降飞行轨迹为某三次函数图象的一部分,则该函数的解析式为( ) A、y= ﹣ x B、y= x3﹣ x C、y= x3﹣x D、y=﹣ x3+ x8. 已知A,B两地相距150千米,某人开汽车以60千米/小时的速度从A地到达B地,在B地停留1小时后再以50千米/小时的速度返回A地,把汽车离开A地的距离x表示为时间t(小时)的函数表达式是( )A、x=60t B、x=60t+50t C、 D、x=9. 已知为上奇函数,当时, , 则当时,( ).
A、y= ﹣ x B、y= x3﹣ x C、y= x3﹣x D、y=﹣ x3+ x8. 已知A,B两地相距150千米,某人开汽车以60千米/小时的速度从A地到达B地,在B地停留1小时后再以50千米/小时的速度返回A地,把汽车离开A地的距离x表示为时间t(小时)的函数表达式是( )A、x=60t B、x=60t+50t C、 D、x=9. 已知为上奇函数,当时, , 则当时,( ).
A、 B、 C、 D、10. 函数 的图像如图所示,则下列结论成立的是() A、a>0,b<0,c>0,d>0 B、a>0,b<0,c<0,d>0 C、a<0,b<0,c<0,d>0 D、a>0,b>0,c>0,d<011.
A、a>0,b<0,c>0,d>0 B、a>0,b<0,c<0,d>0 C、a<0,b<0,c<0,d>0 D、a>0,b>0,c>0,d<011.图中的图象所表示的函数的解析式为( )
 A、y= |x﹣1|(0≤x≤2) B、y= ﹣ |x﹣1|(0≤x≤2) C、y= ﹣|x﹣1|(0≤x≤2) D、y=1﹣|x﹣1|(0≤x≤2)12. 下列图中,画在同一坐标系中,函数y=ax2+bx与y=ax+b(a≠0,b≠0)函数的图象只可能是( )A、
A、y= |x﹣1|(0≤x≤2) B、y= ﹣ |x﹣1|(0≤x≤2) C、y= ﹣|x﹣1|(0≤x≤2) D、y=1﹣|x﹣1|(0≤x≤2)12. 下列图中,画在同一坐标系中,函数y=ax2+bx与y=ax+b(a≠0,b≠0)函数的图象只可能是( )A、 B、
B、 C、
C、 D、
D、 13. 函数y=f(x)的图象如图所示.观察图象可知函数y=f(x)的定义域、值域分别是( )
13. 函数y=f(x)的图象如图所示.观察图象可知函数y=f(x)的定义域、值域分别是( ) A、[﹣5,0]∪[2,6),[0,5] B、[﹣5,6),[0,+∞) C、[﹣5,0]∪[2,6),[0,+∞) D、[﹣5,+∞),[2,5]14. 已知图甲中的图象对应的函数y=f(x),则图乙中的图象对应的函数在下列给出的四式中只可能是( )
A、[﹣5,0]∪[2,6),[0,5] B、[﹣5,6),[0,+∞) C、[﹣5,0]∪[2,6),[0,+∞) D、[﹣5,+∞),[2,5]14. 已知图甲中的图象对应的函数y=f(x),则图乙中的图象对应的函数在下列给出的四式中只可能是( ) A、y=f(|x|) B、y=|f(x)| C、y=f(﹣|x|) D、y=﹣f(|x|)15. 已知a>0且a≠1,函数y=logax,y=ax , y=x+a在同一坐标系中的图象可能是( )A、
A、y=f(|x|) B、y=|f(x)| C、y=f(﹣|x|) D、y=﹣f(|x|)15. 已知a>0且a≠1,函数y=logax,y=ax , y=x+a在同一坐标系中的图象可能是( )A、 B、
B、 C、
C、 D、
D、 16. 函数y=1+ 的图象是( )A、
16. 函数y=1+ 的图象是( )A、 B、
B、 C、
C、 D、
D、
二、填空题
-
17. 在平面角坐标系xOy中,若直线y=2a与函数y=|x-a|-1的图像只有一个交点,则a的值为。18. 若函数f(x)=|2x-2|-b有两个零点,则实数b的取值范围是 .19. 已知函数f(x)=x3﹣3x+1, , 若对∀x1∈[﹣1,3],∃x2∈[0,2],f(x1)≥g(x2),则实数m的取值范围是20. 设函数
①若a=0,则f(x)的最大值为;
②若f(x)无最大值,则实数a的取值范围是。
21. 已知函数y=f(x)的导函数y=f′(x)的图象如图,则y=f(x)有 个极大值点. 22. 二次函数y=ax2+bx+c的图象如图,则a 0;b 0;c 0;b2﹣4ac 0.(填“>”或“<”、“=”)
22. 二次函数y=ax2+bx+c的图象如图,则a 0;b 0;c 0;b2﹣4ac 0.(填“>”或“<”、“=”)
三、综合题
-
23. 某房地产开发公司计划在一楼区内建造一个长方形公园ABCD,公园由长方形的休闲区A1B1C1D1(阴影部分)和环公园人行道组成.已知休闲区A1B1C1D1的面积为4000平方米,人行道的宽分别为4米和10米.
 (1)、若设休闲区的长A1B1=x米,求公园ABCD所占面积S关于x的函数S(x)的解析式;(2)、要使公园所占面积最小,休闲区A1B1C1D1的长和宽该如何设计?24. 已知函数f(x)=ax2﹣ax﹣1(a∈R).(1)、若对任意实数x,f(x)<0恒成立,求实数a的取值范围;(2)、当a>0时,解关于x的不等式f(x)<2x﹣3.25. 某村投资128万元建起了一处生态采摘园,预计在经营过程中,第一年支出10万元,以后每年支出都比上一年增加4万元,从第一年起每年的销售收入都为76万元.设y表示前n(n∈N*)年的纯利润总和(利润总和=经营总收入﹣经营总支出﹣投资).(1)、该生态园从第几年开始盈利?(2)、该生态园前几年的年平均利润最大,最大利润是多少?26. 甲厂根据以往的生产销售经验得到下面有关生产销售的关系:厂里的固定成本为2.8万元,每生产1百台的生产成本为1万元,每生产产品x(百台),其总成本为G(x)(万元)(总成本=固定成本+生产成本).如果销售收入R(x)= ,且该产品产销平衡(即生产的产品都能卖掉),请完成下列问题:(1)、写出利润函数y=f(x)的解析式(利润=销售收入﹣总成本);(2)、甲厂生产多少台新产品时,可使盈利最多?
(1)、若设休闲区的长A1B1=x米,求公园ABCD所占面积S关于x的函数S(x)的解析式;(2)、要使公园所占面积最小,休闲区A1B1C1D1的长和宽该如何设计?24. 已知函数f(x)=ax2﹣ax﹣1(a∈R).(1)、若对任意实数x,f(x)<0恒成立,求实数a的取值范围;(2)、当a>0时,解关于x的不等式f(x)<2x﹣3.25. 某村投资128万元建起了一处生态采摘园,预计在经营过程中,第一年支出10万元,以后每年支出都比上一年增加4万元,从第一年起每年的销售收入都为76万元.设y表示前n(n∈N*)年的纯利润总和(利润总和=经营总收入﹣经营总支出﹣投资).(1)、该生态园从第几年开始盈利?(2)、该生态园前几年的年平均利润最大,最大利润是多少?26. 甲厂根据以往的生产销售经验得到下面有关生产销售的关系:厂里的固定成本为2.8万元,每生产1百台的生产成本为1万元,每生产产品x(百台),其总成本为G(x)(万元)(总成本=固定成本+生产成本).如果销售收入R(x)= ,且该产品产销平衡(即生产的产品都能卖掉),请完成下列问题:(1)、写出利润函数y=f(x)的解析式(利润=销售收入﹣总成本);(2)、甲厂生产多少台新产品时,可使盈利最多?
