2016-2017学年江苏省南京市鼓楼区七年级上学期期中数学试卷

试卷更新日期：2017-02-15 类型：期中考试

进入出卷网下载

一、选择题

1. ﹣3的绝对值是（）

A、﹣3 B、3 C、±3 D、﹣ $\frac{1}{3}$

查看试题解析
2. 如图，检测4个足球，其中超过标准质量的克数记为正数，不足标准质量的克数记为负数，从轻重的角度看，最接近标准的是（）

A、 B、 C、 D、

查看试题解析
3. 2016年10月16日上午7：45南京马拉松正式开跑，约21000名中外运动爱好者参加了此次活动.21000用科学记数法可表示为（）

A、0.21×10⁵ B、0.21×10⁴ C、2.1×10⁴ D、2.1×10³

查看试题解析
4. 下列各算式中，合并同类项正确的是（）

A、x²+x²=2x² B、x²+x²=x⁴ C、2x²﹣x²=2 D、2x²﹣x²=2x

查看试题解析
5. 单项式﹣ $\frac{2^{3} a^{2} b}{5}$ 的次数是（）

A、﹣2³ B、﹣ $\frac{8}{5}$ C、6 D、3

查看试题解析
6. 把一张厚度为0.1mm的纸对折8次后厚度接近于（）

A、0.8mm B、2.6cm C、2.6mm D、0.1⁸mm

查看试题解析

二、填空题

7. ﹣ $\frac{2}{3}$ 的倒数是．

查看试题解析
8. 在﹣4， $\frac{1}{2}$ ，0，π，1，﹣ $\frac{22}{7}$ ，1. $\dot{3}$ 这些数中，是无理数的是．

查看试题解析
9. 比较大小：﹣ $\frac{2}{3}$ ﹣ $\frac{1}{2}$ （填“＜”、“=”、“＞”）．

查看试题解析
10. 一筐苹果总重x千克，筐本身重2千克，若将苹果平均分成5份，则每份重千克．

查看试题解析
11. 写出两个无理数，使它们的和为有理数．

查看试题解析
12. 如图，若输入的x的值为1，则输出的y值为

查看试题解析
13. 若x²﹣2x﹣1=2，则代数式2x²﹣4x的值为

查看试题解析
14. 数轴上点A表示的数是﹣1，点B到点A的距离为2个单位，则B点表示的数是

查看试题解析
15.
如图，下列图形是将正三角形按一定规律排列，则第5个图形中所有正三角形的个数有．

查看试题解析
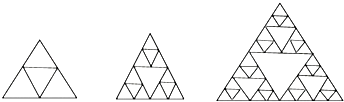16.
如图所示的牌子上有两个整数“1和﹣1”，请你运用有关数学知识，用一句话对这两个整数进行描述（要求不能出现与牌子上相同的数字），请写出两种方案：
①；
② ．

查看试题解析

三、解答题

17. 计算：

(1)、﹣3﹣（﹣4）+2；

(2)、（﹣6）÷2×（﹣ $\frac{1}{2}$ ）；

(3)、（﹣ $\frac{1}{2}$ + $\frac{5}{6}$ ﹣ $\frac{7}{12}$ ）×（﹣24）；

(4)、﹣1⁴﹣7÷[2﹣（﹣3）²]．

查看试题解析
18. 化简：5（3a﹣b）﹣（﹣a+3b）．

查看试题解析
19. 先化简，再求值：3x²y﹣[2x²y﹣3（2xy﹣x²y）﹣xy]，其中x=﹣ $\frac{1}{2}$ ，y=2．

查看试题解析
20. 任意想一个数，把这个数乘2后减8，然后除以4，再减去原来所想的那个数的 $\frac{1}{2}$ ，小明说所得结果一定是﹣2．请你通过列式计算说明小明说的正确．

查看试题解析
21. 解答题

(1)、一个数的绝对值是指在数轴上表示这个数的点到的距离；

(2)、若|a|=﹣a，则a0；

(3)、有理数a、b在数轴上的位置如图所示，请化简|a|+|b|+|a+b|．

查看试题解析
22. 2016年9月15日晚，正值中秋佳节，我国“天宫二号”空间实验室顺利升空．同学们倍受鼓舞，某同学绘制了如图所示的火箭模型截面图，下面是梯形，中间是长方形，上面是三角形．

(1)、用含有a、b的代数式表示该截面的面积S；

(2)、当a=2.8cm，b=2.2cm时，求这个截面的面积．

查看试题解析
23. 某原料仓库一天的原料进出记录如下表（运进用正数表示，运出用负数表示）：
进出数量（单位：吨）
﹣3
4
﹣1
2
﹣5
进出次数
2
1
3
3
2

(1)、这天仓库的原料比原来增加了还是减少？请说明理由；

(2)、根据实际情况，现有两种方案：
方案一：运进每吨原料费用5元，运出每吨原料费用8元；
方案二：不管运进还是运出费用都是每吨原料6元；从节约运费的角度考虑，选用哪一种方案比较合适．

(3)、在（2）的条件下，设运进原料共a吨，运出原料共b吨，a、b之间满足怎样的关系时，两种方案的运费相同．

查看试题解析
24. 如图，在一张长方形纸条上画一条数轴．

(1)、若折叠纸条，数轴上表示﹣3的点与表示1的点重合，则折痕与数轴的交点表示的数为；

(2)、若经过某次折叠后，该数轴上的两个数a和b表示的点恰好重合，则折痕与数轴的交点表示的数为（用含a，b的代数式表示）；

(3)、若将此纸条沿虚线处剪开，将中间的一段纸条对折，使其左右两端重合，这样连续对折n次后，再将其展开，请分别求出最左端的折痕和最右端的折痕与数轴的交点表示的数．（用含n的代数式表示）

查看试题解析
25. 【探索新知】
已知平面上有n（n为大于或等于2的正整数）个点A₁ ， A₂ ， A₃ ， …A_n ，从第1个点A1开始沿直线滑动到另一个点，且同时满足以下三个条件：①每次滑动的距离都尽可能最大；②n次滑动将每个点全部到达一次；③滑动n次后必须回到第1个点A₁ ，我们称此滑动为“完美运动”，且称所有点为“完美运动”的滑动点，记完成n个点的“完美运动”的路程之和为S_n ．

(1)、如图1，滑动点是边长为a的等边三角形三个顶点，此时S₃=；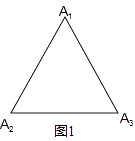

(2)、如图2，滑动点是边长为a，对角线（线段A₁A₂、A₂A₄）长为b的正方形四个顶点，此时S₄= ．
【深入研究】
现有n个点恰好在同一直线上，相邻两点距离都为1，

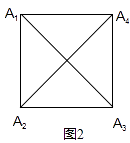(3)、如图3，当n=3时，直线上的点分别为A₁、A₂、A₃ ．
为了完成“完美运动”，滑动的步骤给出如图4所示的两种方法：
方法1：A₁→A₃→A₂→A₁ ，方法2：A₁→A₂→A₃→A₁ ．
①其中正确的方法为．
A．方法1 B．方法2 C．方法1和方法2
②完成此“完美运动”的S₃= ．

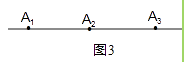
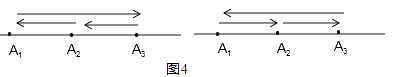(4)、当n分别取4，5时，对应的S₄= ， S₅=

(5)、若直线上有n个点，请用含n的代数式表示S_n ．

查看试题解析

进出数量（单位：吨）	﹣3	4	﹣1	2	﹣5
进出次数	2	1	3	3	2