2016-2017学年黑龙江省哈尔滨四十七中七年级上学期期中数学试卷(五四学制)
试卷更新日期:2017-02-15 类型:期中考试
一、选择题
-
1. 下列方程中是一元一次方程的是( )A、x+3=y+2 B、x+3=3﹣x C、 =1 D、x2﹣1=02. 下列图中,∠1与∠2属于对顶角的是( )A、
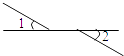 B、
B、 C、
C、 D、
D、 3. 下列等式变形中,结果不正确的是( )A、如果a=b,那么a+2b=3b B、如果a=3,那么a﹣k=3﹣k C、如果m=n,那么mc2=nc2 D、如果mc2=nc2 , 那么m=n4. 如图是2016年巴西奥运会的吉祥物维尼修斯,下列图案中,是通过如图平移得到的图案是( )
3. 下列等式变形中,结果不正确的是( )A、如果a=b,那么a+2b=3b B、如果a=3,那么a﹣k=3﹣k C、如果m=n,那么mc2=nc2 D、如果mc2=nc2 , 那么m=n4. 如图是2016年巴西奥运会的吉祥物维尼修斯,下列图案中,是通过如图平移得到的图案是( ) A、
A、 B、
B、 C、
C、 D、
D、 5. 如图,a∥b,若∠1=50°,则∠2的度数为( )
5. 如图,a∥b,若∠1=50°,则∠2的度数为( ) A、50° B、120° C、130° D、140°6. 粉刷一个房间甲单独做4天完成,乙单独做6天完成,丙单独做12天完成.甲先单独做2天后有事离开,接下来乙、丙共同完成,则乙、丙合作所需要的天数为( )A、1 B、2 C、3 D、47. 如图,已知直线AB,CD相交于点O,OA平分∠EOC,∠EOC=70°,则∠BOD的度数等于( )
A、50° B、120° C、130° D、140°6. 粉刷一个房间甲单独做4天完成,乙单独做6天完成,丙单独做12天完成.甲先单独做2天后有事离开,接下来乙、丙共同完成,则乙、丙合作所需要的天数为( )A、1 B、2 C、3 D、47. 如图,已知直线AB,CD相交于点O,OA平分∠EOC,∠EOC=70°,则∠BOD的度数等于( )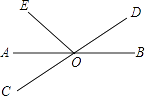 A、30° B、35° C、20° D、4°8. 将一直角三角板与两边平行的纸条如图所示放置,有下列结论:
A、30° B、35° C、20° D、4°8. 将一直角三角板与两边平行的纸条如图所示放置,有下列结论:①∠1=∠2;②∠3=∠4;③∠2+∠4=90°;④∠4+∠5=180°.
其中正确的个数为( )
 A、1 B、2 C、3 D、49. 一架飞机在两城间飞行,顺风航行要5.5小时,逆风航行要6小时,风速为24千米/时,设飞机无风时的速度为每小时x千米,则下列方程正确是( )A、5.5(x﹣24)=6(x+24) B、= C、5.5(x+24)=6(x﹣24) D、= ﹣2410. 下列命题中:
A、1 B、2 C、3 D、49. 一架飞机在两城间飞行,顺风航行要5.5小时,逆风航行要6小时,风速为24千米/时,设飞机无风时的速度为每小时x千米,则下列方程正确是( )A、5.5(x﹣24)=6(x+24) B、= C、5.5(x+24)=6(x﹣24) D、= ﹣2410. 下列命题中:①点到直线的距离是指这点到直线的垂线段;
②两直线被第三条直线所截,同位角相等;
③平移时,连接对应点的线段平行且相等;
④在同一平面内,有且只有一条直线与已知直线垂直;
⑤对顶角相等;
⑥过一点有且只有一条直线与已知直线平行.
其中真命题的个数为( )
A、1 B、2 C、3 D、4二、填空题
-
11. 已知关于x的方程5xm+2+3=0是一元一次方程,则m= .12. 如图,直线a、b相交,∠1=36度,则∠2=度.
 13. 命题“两直线平行,同位角相等”的题设是 , 结论是 .14. 当x=时,整式3x﹣1与2x+1互为相反数.15. 七年级男生入住的一楼有x间房间,如果每间住6人,恰好空出一间;如果每间住5人就有4人没有房间住,则x的值为 .16. 如图,AD是∠EAC的平分线,AD∥BC,∠B=40°,则∠DAC的度数为
13. 命题“两直线平行,同位角相等”的题设是 , 结论是 .14. 当x=时,整式3x﹣1与2x+1互为相反数.15. 七年级男生入住的一楼有x间房间,如果每间住6人,恰好空出一间;如果每间住5人就有4人没有房间住,则x的值为 .16. 如图,AD是∠EAC的平分线,AD∥BC,∠B=40°,则∠DAC的度数为 17. 如图,将三角板与两边平行的直尺(EF∥HG)贴在一起,使三角板的直角顶点C(∠ACB=90°)在直尺的一边上,若∠2=55°,则∠1的度数等于 .
17. 如图,将三角板与两边平行的直尺(EF∥HG)贴在一起,使三角板的直角顶点C(∠ACB=90°)在直尺的一边上,若∠2=55°,则∠1的度数等于 . 18. 一个两位数的十位数字与个位数字的和是7,把这个两位数加上45后,结果恰好成为数字对调后组成的两位数,则这个两位数是 .19. 两个角α和β的两边互相平行,且一个角α比另一个角β的 多20°,则这个角α的度数为度.20. 如图,三角形DEF是三角形ABC沿射线BC平移的得到的,BE=2,DE与AC交于点G,且满足DG=2GE.若三角形CEG的面积为1,CE=1,则点G到AD的距离为 .
18. 一个两位数的十位数字与个位数字的和是7,把这个两位数加上45后,结果恰好成为数字对调后组成的两位数,则这个两位数是 .19. 两个角α和β的两边互相平行,且一个角α比另一个角β的 多20°,则这个角α的度数为度.20. 如图,三角形DEF是三角形ABC沿射线BC平移的得到的,BE=2,DE与AC交于点G,且满足DG=2GE.若三角形CEG的面积为1,CE=1,则点G到AD的距离为 .
三、解答题
-
21. 解方程(1)、6x﹣7=4x﹣5(2)、8x=﹣2(x+4)(3)、 ﹣1= .22. 三角形ABC在正方形网格中的位置如图所示,网格中每个小方格的边长为1个单位长度,请根据下列提示作图
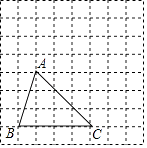 (1)、将三角形ABC向上平移3个单位长度,再向右平移2个单位长度得到三角形A'B'C',画出三角形A'B'C'.(2)、过点B'画A'C'的垂线,垂足为H.23. 完成下面推理过程.在括号内的横线上填空或填上推理依据.
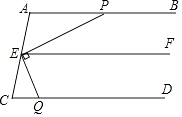
(1)、将三角形ABC向上平移3个单位长度,再向右平移2个单位长度得到三角形A'B'C',画出三角形A'B'C'.(2)、过点B'画A'C'的垂线,垂足为H.23. 完成下面推理过程.在括号内的横线上填空或填上推理依据.如图,已知:AB∥EF,EP⊥EQ,∠EQC+∠APE=90°,求证:AB∥CD
证明:∵AB∥EF
∴∠APE=()
∵EP⊥EQ
∴∠PEQ=()
即∠QEF+∠PEF=90°
∴∠APE+∠QEF=90°
∵∠EQC+∠APE=90°
∴∠EQC=
∴EF∥()
∴AB∥CD()
 24. 某车间22名工人生产螺钉和螺母,每人每天平均生产螺钉1200个或螺母2000个,一个螺钉要配两个螺母.为了使每天的产品刚好配套,应该分配多少名工人生产螺钉,多少名工人生产螺母?25. 如图,直线AB、CD相交于点O,OE平分∠AOC,OF⊥OE于O,且∠DOF=75°,求∠BOD的度数.
24. 某车间22名工人生产螺钉和螺母,每人每天平均生产螺钉1200个或螺母2000个,一个螺钉要配两个螺母.为了使每天的产品刚好配套,应该分配多少名工人生产螺钉,多少名工人生产螺母?25. 如图,直线AB、CD相交于点O,OE平分∠AOC,OF⊥OE于O,且∠DOF=75°,求∠BOD的度数. 26. 恺桐超市购进一批四阶魔方,按进价提高40%后标价,为了让利于民,增加销量,超市决定打八折出售,这时每个魔方的售价为28元.(1)、求魔方的进价?(2)、超市卖出一半后,正好赶上双十一促销,商店决定将剩下的魔方以每3个80元的价格出售,很快销售一空,这批魔方超市共获利2800元,求该超市共购进四阶魔方多少个?27. 已知AM∥CN,点B为平面内一点,AB⊥BC于B.(1)、如图1,直接写出∠A和∠C之间的数量关系;
26. 恺桐超市购进一批四阶魔方,按进价提高40%后标价,为了让利于民,增加销量,超市决定打八折出售,这时每个魔方的售价为28元.(1)、求魔方的进价?(2)、超市卖出一半后,正好赶上双十一促销,商店决定将剩下的魔方以每3个80元的价格出售,很快销售一空,这批魔方超市共获利2800元,求该超市共购进四阶魔方多少个?27. 已知AM∥CN,点B为平面内一点,AB⊥BC于B.(1)、如图1,直接写出∠A和∠C之间的数量关系; (2)、如图2,过点B作BD⊥AM于点D,求证:∠ABD=∠C;
(2)、如图2,过点B作BD⊥AM于点D,求证:∠ABD=∠C; (3)、如图3,在(2)问的条件下,点E、F在DM上,连接BE、BF、CF,BF平分∠DBC,BE平分∠ABD,若∠FCB+∠NCF=180°,∠BFC=3∠DBE,求∠EBC的度数.
(3)、如图3,在(2)问的条件下,点E、F在DM上,连接BE、BF、CF,BF平分∠DBC,BE平分∠ABD,若∠FCB+∠NCF=180°,∠BFC=3∠DBE,求∠EBC的度数.