2017高考数学备考复习(理科)专题二十二:几何证明选讲
试卷更新日期:2017-02-14 类型:一轮复习
一、单选题
-
1. 如图,⊙O与⊙P相交于A,B两点,点P在⊙O上,⊙O的弦BC切⊙P于点B,CP及其延长线交⊙P于D,E两点,过点E作EF⊥CE交CB延长线于点F.若CD=2,CB=2 , 则EF的长为( )
 A、 B、 C、 D、2. 如图,某花木场有一块等腰梯形ABCD的空地,其各边中点分别是E、F、G、H,测得对角线BD=12米,现想用篱笆围成四边形EFGH的场地,则需用的篱笆总长度是( )
A、 B、 C、 D、2. 如图,某花木场有一块等腰梯形ABCD的空地,其各边中点分别是E、F、G、H,测得对角线BD=12米,现想用篱笆围成四边形EFGH的场地,则需用的篱笆总长度是( ) A、12米 B、24米 C、36米 D、48米3. 下列命题中正确的命题个数为( )
A、12米 B、24米 C、36米 D、48米3. 下列命题中正确的命题个数为( )①如果一条直线与一平面平行,那么这条直线与平面内的任意直线平行;
②如果一条直线与一个平面相交,那么这条直线与这个平面内无数条直线垂直;
③过平面外一点有且只有一条直线与平面平行;
④一条直线上有两点到一个平面的距离相等,则这条直线平行于这个平面.
A、0 B、1 C、2 D、34.如图所示,已知AA′∥BB′∥CC′,AB:BC=1:3,那么下列等式成立的是( )
 A、AB=2A′B′ B、3A′B′=B′C′ C、BC=B′C′ D、AB=A′B′5. 如图,E是平行四边形ABCD的边AB延长线上一点,且DC:BE=3:2,则AD:BF=( )
A、AB=2A′B′ B、3A′B′=B′C′ C、BC=B′C′ D、AB=A′B′5. 如图,E是平行四边形ABCD的边AB延长线上一点,且DC:BE=3:2,则AD:BF=( ) A、 B、 C、 D、6.
A、 B、 C、 D、6.在△ABC中∠BAC=90°,D是BC边的中点,AE⊥AD,AE交CB的延长线于E,则下面结论中正确的是( )
 A、△AED∽△ACB B、△AEB∽△ACD C、△BAE∽△ACE D、△AEC∽△DAC7.
A、△AED∽△ACB B、△AEB∽△ACD C、△BAE∽△ACE D、△AEC∽△DAC7.如图,四边形ABCD内接于圆O,且AC、BD交于点E,则此图形中一定相似的三角形有( )对.
 A、0 B、3 C、2 D、18. 如图,D、E分别在AB、AC上,下列条件不能判定△ADE与△ABC相似的有( )
A、0 B、3 C、2 D、18. 如图,D、E分别在AB、AC上,下列条件不能判定△ADE与△ABC相似的有( ) A、∠AED=∠B B、 C、 D、DE∥BC9.
A、∠AED=∠B B、 C、 D、DE∥BC9.如图,若△ACD~△ABC,则下列式子中成立的是( )
 A、CD2=AD•DB B、AC2=AD•AB C、AC•AD=AB•CD D、AC•BC=AB•AD10. 如图,PC是⊙O的切线,C为切点,PAB为割线,PC=2,PA=1,∠P=60°,则BC=( )
A、CD2=AD•DB B、AC2=AD•AB C、AC•AD=AB•CD D、AC•BC=AB•AD10. 如图,PC是⊙O的切线,C为切点,PAB为割线,PC=2,PA=1,∠P=60°,则BC=( ) A、3 B、2 C、3 D、211.
A、3 B、2 C、3 D、211.如图,PA切⊙O于A,PB切⊙O于B,OP交⊙O于C,下列结论中,错误的是( )
 A、∠1=∠2 B、PA=PB C、AB⊥OP D、PA2=PC•PO12. 如图,A、B是⊙O上的两点,AC是⊙O的切线,∠B=70°,则∠BAC等于( )
A、∠1=∠2 B、PA=PB C、AB⊥OP D、PA2=PC•PO12. 如图,A、B是⊙O上的两点,AC是⊙O的切线,∠B=70°,则∠BAC等于( ) A、70° B、35° C、20° D、10°13. 如图,四边形ABCD内接于圆O,∠BOD=110°,∠BCD等于( )
A、70° B、35° C、20° D、10°13. 如图,四边形ABCD内接于圆O,∠BOD=110°,∠BCD等于( ) A、100° B、110° C、125° D、135°14. 如图,△ABC是圆的内接三角形,∠BAC的平分线交圆于点D,交BC于E,过点B的圆的切线与AD的延长线交于点F,在上述条件下,给出下列四个结论:
A、100° B、110° C、125° D、135°14. 如图,△ABC是圆的内接三角形,∠BAC的平分线交圆于点D,交BC于E,过点B的圆的切线与AD的延长线交于点F,在上述条件下,给出下列四个结论:①BD平分∠CBF;
②FB2=FD•FA;
③AE•CE=BE•DE;
④AF•BD=AB•BF.

所有正确结论的序号是( )
A、①② B、③④ C、①②③ D、①②④15. 如图,AB、CD是⊙O的两条弦,且AB是线段CD的中垂线,已知AB=6,CD=2 ,则线段AC的长度为( ) A、5 B、 C、 D、3
A、5 B、 C、 D、3二、填空题
-
16. 如图,P是圆O外一点,过P引圆O的两条割线PAB、PCD,PA=AB= , CD=3,则PC= .
 17.
17.如图,在△ABC中,MN∥DE∥BC,若AE:EC=7:3,则DB:AB的值为 .
 18. 如图,在半径为 的⊙O中,弦AB,CD相交于点P,PA=PB=2,PD=1,则圆心O到弦CD的距离为 .
18. 如图,在半径为 的⊙O中,弦AB,CD相交于点P,PA=PB=2,PD=1,则圆心O到弦CD的距离为 .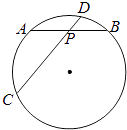 19. (几何证明选做题)
19. (几何证明选做题)如图,弦AB与CD相交于⊙O内一点E,过E作BC的平行线与AD的延长线相交于点P.已知PD=2DA=2,则PE= .
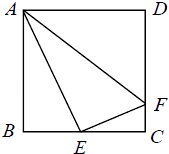
 20. 如图,在正方形ABCD中,E是BC的中点,F是CD上一点,且CF= CD,下列结论:
20. 如图,在正方形ABCD中,E是BC的中点,F是CD上一点,且CF= CD,下列结论:①∠BAE=30°,②△ABE~△AEF,③AE⊥EF,④△ADF~△ECF.
其中正确的有 .
三、综合题
-
21. 如图,AB、CD是圆的两条平行弦,BE∥AC,BE交CD于E、交圆于F,过A点的切线交DC的延长线于P,PC=ED=1,PA=2.
 (1)、求AC的长;(2)、试比较BE与EF的长度关系.22. 选修4﹣1:几何证明选讲
(1)、求AC的长;(2)、试比较BE与EF的长度关系.22. 选修4﹣1:几何证明选讲如图,⊙O和⊙O′相交于A,B两点,过A作两圆的切线分别交两圆于C、D两点,连接DB并延长交⊙O于点E.证明:
 (1)、AC•BD=AD•AB;(2)、AC=AE.23. 如图,平行四边形ABCD中,AE:EB=1:2.
(1)、AC•BD=AD•AB;(2)、AC=AE.23. 如图,平行四边形ABCD中,AE:EB=1:2. (1)、求△AEF与△CDF的周长比;(2)、如果△AEF的面积等于6cm2 , 求△CDF的面积.
(1)、求△AEF与△CDF的周长比;(2)、如果△AEF的面积等于6cm2 , 求△CDF的面积.

