2017高考数学备考复习（理科）专题十八：统计与统计案例

试卷更新日期：2017-02-14 类型：一轮复习

进入出卷网下载

一、单选题

1.
设 $(x_{1} ， y_{1})$ ， $(x_{2} ， y_{2})$ ，， $(x_{n} ， y_{n})$ 是变量x和y的n个样本点，直线l是由这些样本点通过最小二乘法得到的线性回归直线（如图），以下结论中正确的是（）

A、x和y相关系数为直线l的斜率 B、x和y的相关系数在0到1之间 C、当n为偶数时，分布在l两侧的样本点的个数一定相同 D、直线l过点 $(\bar{x} ， \bar{y})$

查看试题解析
2. 某学校为了调查高三年级的200名文科学生完成课后作业所需时间，采取了两种抽样调查的方式：第一种由学生会的同学随机抽取20名同学进行调查；第二种由教务处对该年级的文科学生进行编号，从001到200，抽取学号最后一位为2的同学进行调查，则这两种抽样的方法依次为（）

A、分层抽样，简单随机抽样 B、简单随机抽样，分层抽样 C、分层抽样，系统抽样 D、简单随机抽样，系统抽样

查看试题解析
3. 对100只小白鼠进行某种激素试验，其中雄性小白鼠、雌性小白鼠对激素的敏感情况统计得到如下列联表

雄性
雌性
总计
敏感
50
25
75
不敏感
10
15
25
总计
60
40
100
由 $K^{2} = \frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)} \approx 5.56$
附表：
P( $k^{2} \geq k$ )
0.050
0.010
0.001
k
3.841
6.635
10.828
则下列说法正确的是( )

A、在犯错误的概率不超过0.1%的前提下认为“对激素敏感与性别有关”； B、在犯错误的概率不超过0.1%的前提下认为“对激素敏感与性别无关”； C、有95%以上的把握认为“对激素敏感与性别有关”； D、有95%以上的把握认为“对激素敏感与性别无关”；

查看试题解析
4. 已知数据 $x_{1} ， x_{2} ，， x_{3} \dots x_{n}$ 是上海普通职工n $(n \geq 3 ， n \in N^{*})$ 个人的年收入，设n个数据的中位数为x，平均数为y，方差为z，如果再加上世界首富的年收入 $x_{n + 1}$ ，则这n+1个数据中，下列说法正确的是 ( )

A、年收入平均数大大增加，中位数一定变大，方差可能不变 B、年收入平均数大大增加，中位数可能不变，方差变大 C、年收入平均数大大增加，中位数可能不变，方差也不变 D、年收入平均数可能不变，中位数可能不变，方差可能不变

查看试题解析
5. 我国古代数学名著《九章算术》有“米谷粒分”题：粮仓开仓收粮，有人送来米1534石，验得米内夹谷，抽样取米一把，数得254粒内夹谷28粒，则这批米内夹谷约为（）

A、134石 B、169石 C、338石 D、1365石

查看试题解析
6. 已知变量 $x$ 和 $y$ 满足关系 $y = - 0.1 x + 1$ ，变量 $y$ 与 $z$ 正相关. 下列结论中正确的是（）

A、 $x$ 与 $y$ 负相关， $x$ 与 $z$ 负相关 B、 $x$ 与 $y$ 正相关， $x$ 与 $z$ 正相关 C、 $x$ 与 $y$ 正相关， $x$ 与 $z$ 负相关 D、 $x$ 与 $y$ 负相关， $x$ 与 $z$ 正相关

查看试题解析
7. 下表是一位母亲给儿子作的成长记录：
年龄/周岁
3
4
5
6
7
8
9
身高/cm
94.8
104.2
108.7
117.8
124.3
130.8
139.1
根据以上样本数据，她建立了身高 y （cm）与年龄x（周岁）的线性回归方程为 $\overset{\land}{y}$ =7.19x+73.93，给出下列结论：
①y与x具有正的线性相关关系；
②回归直线过样本的中心点（42，117.1）；
③儿子10岁时的身高是145.83 cm；
④儿子年龄增加1周岁，身高约增加 7.19 cm.
其中，正确结论的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
8.
某高校《统计》课程的教师随机给出了选该课程的一些情况，具体数据如下：

非统计专业
统计专业
男
13
10
女
7
20
为了判断选修统计专业是否与性别有关，根据表中数据，得，因为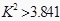，所以可以判定选修统计专业与性别有关.那么这种判断出错的可能性为（）

A、5% B、95% C、1% D、99%

查看试题解析
9. 某学校高一、高二、高三年级的学生人数分别为900、900、1200人，现用分层抽样的方法从该校高中三个年级的学生中抽取容量为50的样本，则应从高三年级抽取的学生人数为（　　）

A、15 B、20 C、25 D、30

查看试题解析
10. 采用系统抽样方法从1000人中抽取50人做问卷调查，为此将他们随机编号为1，2，…，1000，适当分组后在第一组采用简单随机抽样的方法抽到的号码为8．抽到的50人中，编号落入区间[1，400]的人做问卷A，编号落入区间[401，750]的人做问卷B，其余的人做问卷C．则抽到的人中，做问卷C的人数为（　　）

A、12 B、13 C、14 D、15

查看试题解析
11.
一批产品抽50件测试，其净重介于13克与19克之间，将测试结果按如下方式分成六组：第一组，净重大于等于13克且小于14克；第二组，净重大于等于14克且小于15克；…第六组，净重大于等于18克且小于19克．如图是按上述分组方法得到的频率分布直方图．设净重小于17克的产品数占抽取数的百分比为x，净重大于等于15克且小于17克的产品数为y，则从频率分布直方图中可分析出x和y分别为（　　）

A、0.9，35 B、0.9，45 C、0.1，35 D、0.1，45

查看试题解析
12.
为了研究某高校大学5000名新生的视力情况，随机地抽查了该校100名进校新生的视力情况，得到其频率分布直方图如右图，若规定视力低于5.0的学生属[于近视学生，则估计该校新生中不是近视的人数约为（　　）

A、300人 B、400人 C、600人 D、1000人

查看试题解析
13. 总体编号为01，02，…，19，20的20个个体组成．利用下面的随机数表选取5个个体，选取方法是从随机数表第1行的第5列和第6列数字开始由左到右依次选取两个数字，则选出来的第5个个体的编号是（　　）
7816 6572 0802 6314 0702 4369 9728 0198
3204 9234 4935 8200 3623 4869 6938 7481．

A、08 B、07 C、02 D、01

查看试题解析
14. 设某大学的女生体重y（单位：kg）与身高x（单位：cm）具有线性相关关系，根据一组样本数据（x_i ， y_i）（i=1，2，…，n），用最小二乘法建立的回归方程为 $\hat{y}$ =0.85x﹣85.71，则下列结论中不正确的是（）

A、y与x具有正的线性相关关系 B、回归直线过样本点的中心（ $\bar{x}$ ， $\bar{y}$ ） C、若该大学某女生身高增加1cm，则其体重约增加0.85kg D、若该大学某女生身高为170cm，则可断定其体重必为58.79kg

查看试题解析
15. 总体由编号为01，02，…，19，20的20个个体组成．利用下面的随机数表选取5个个体，选取方法从随机数表第1行的第5列和第6列数字开始由左到右依次选取两个数字，则选出来的第5个个体的编号为（）
7816
6572
0802
6314
0702
4369
9728
0198
3204
9234
4935
8200
3623
4869
6938
7481

A、08 B、07 C、02 D、01

查看试题解析

二、填空题

16.
甲、乙、丙、丁4位同学各自对A ， B两变量做回归分析，分别得到散点图与残差平方和 $\sum_{i = 1}^{n} {(y_{i} - {\hat{y}}_{i})}^{2}$ ，如下表：

甲
乙
丙
丁
散点图
残差平方和
115
106
124
103
则同学的试验结果体现拟合A ， B两变量关系的模型拟合精度最高.

查看试题解析
17. 为了调查患慢性气管炎是否与吸烟有关，调查了339名50岁以上的人，调查结果如下表

患慢性气管炎
未患慢性气管炎
合计
吸烟
43
162
205
不吸烟
13
121
134
合计
56
283
339
根据列联表数据，求得K² = .

查看试题解析
18. 在一次有奖明信片的100000个有机会中奖的号码（编号00000﹣99999）中，邮政部门按照随机抽取的方式确定后两位是23的作为中奖号码，这是运用了抽样方法．

查看试题解析
19. 为了调查某野生动物保护区内某种野生动物的数量，调查人员逮到这种动物1200只作过标记后放回，一星期后，调查人员再次逮到该种动物1000只，其中作过标记的有100只，估算保护区有这种动物只．

查看试题解析
20. 某单位为了了解用电量y度与气温x℃之间的关系，随机统计了某4天的用电量与当天气温．
气温（℃）
14
12
8
6
用电量（度）
22
26
34
38
由表中数据得线性方程 $\overset{\land}{y}$ = $\overset{\land}{a}$ + $\overset{\land}{b}$ x中 $\overset{\land}{b}$ =﹣2，据此预测当气温为5℃时，用电量的度数约为

查看试题解析

三、综合题

21. 假设关于某设备的使用年限x和支出的维修费用y（万元），有如下表的统计资料：
使用年限x
2
3
4
5
6
维修费用y
2.2
3.8
5.5
6.5
7.0
若由资料知y对x呈线性相关关系，试求：

(1)、
线性回归方程 .

(2)、估计使用年限为10年时，维修费用是多少.

(3)、计算总偏差平方和、残差平方和及回归平方和.

(4)、
求并说明模型的拟合效果.

查看试题解析
22. 十八届五中全会公报指出：努力促进人口均衡发展，坚持计划生育的基本国策，完善人口发展战略，全面实施一对夫妇可生育两个孩子的政策，提高生殖健康、妇幼保健、托幼等公共服务水平．为了解适龄公务员对放开生育二胎政策的态度，某部门随机调查了100位30到40岁的公务员，得到情况如下表：
男公务员
女公务员
生二胎
40
20
不生二胎
20
20

(1)、是否有95%以上的把握认为“生二胎与性别有关”，并说明理由；

(2)、把以上频率当概率，若从社会上随机抽取3位30到40岁的男公务员，记其中生二胎的人数为X，求随机变量X的分布列，数学期望．
附：K²= $\frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}$
P（K²≥k₀）
0.050
0.010
0.001
k₀
3.841
6.635
10.828

查看试题解析
23. 为了解少年儿童的肥胖是否与常喝碳酸饮料有关，现对30名六年级学生进行了问卷调查，得到如下列联表（平均每天喝500ml以上为常喝，体重超过50kg为肥胖）：
常喝
不常喝
合计
肥胖
2
不肥胖
18
合计
30
已知在全部30人中随机抽取1人，抽到肥胖的学生的概率为 $\frac{4}{15}$ ．

(1)、请将上面的列联表补充完整；

(2)、是否有99.5%的把握认为肥胖与常喝碳酸饮料有关？说明你的理由；

(3)、现从常喝碳酸饮料且肥胖的学生中（2名女生），抽取2人参加电视节目，则正好抽到一男一女的概率是多少
P（K²≥k）
0.15
0.10
0.05
0.025
0.010
0.005
0.001
K
2.072
2.706
3.841
5.024
6.635
7.879
10.828
（参考公式：K²= $\frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}$ ，其中n=a+b+c+d）

查看试题解析

四、解答题

24.
某校高一学生共有500人，为了了解学生的历史学习情况，随机抽取了50名学生，对他们一年来4次考试的历史平均成绩进行统计，得到频率分布直方图如图所示，后三组频数成等比数列．
（1）求第五、六组的频数，补全频率分布直方图；
（2）若每组数据用该组区间中点值（例如区间[70，80）的中点值是
75作为代表，试估计该校高一学生历史成绩的平均分；
（3）估计该校高一学生历史成绩在70～100分范围内的人数．

查看试题解析
25. 我国是世界上严重缺水的国家，某市政府为了鼓励居民节约用水，计划调整居民生活用水收费方案，拟确定一个合理的月用水量标准x（吨），一位居民的月用水量不超过x的部分按平价收费，超出x的部分按议价收费．为了了解居民用水情况，通过抽样，获得了某年100位居民每人的月均用水量（单位：吨），将数据按照[0，0.5），[0.5，1），…，[4，4.5）分成9组，制成了如图所示的频率分布直方图．
（Ⅰ）求直方图中a的值；
（Ⅱ）设该市有30万居民，估计全市居民中月均用水量不低于3吨的人数，并说明理由；
（Ⅲ）若该市政府希望使85%的居民每月的用水量不超过标准x（吨），估计x的值，并说明理由．

查看试题解析

年龄/周岁	3	4	5	6	7	8	9
身高/cm	94.8	104.2	108.7	117.8	124.3	130.8	139.1

7816	6572	0802	6314	0702	4369	9728	0198
3204	9234	4935	8200	3623	4869	6938	7481

	患慢性气管炎	未患慢性气管炎	合计
吸烟	43	162	205
不吸烟	13	121	134
合计	56	283	339

P（K²≥k）	0.15	0.10	0.05	0.025	0.010	0.005	0.001
K	2.072	2.706	3.841	5.024	6.635	7.879	10.828

	雄性	雌性	总计
敏感	50	25	75
不敏感	10	15	25
总计	60	40	100

	非统计专业	统计专业
男	13	10
女	7	20

	甲	乙	丙	丁
散点图
残差平方和	115	106	124	103

气温（℃）	14	12	8	6
用电量（度）	22	26	34	38