2016-2017学年江西省宜春三中高三上学期期中数学试卷(理科)
试卷更新日期:2017-02-13 类型:期中考试
一、选择题
-
1. 若集合M={y|y=3x},N={x|y= },则M∩N=( )A、[0, ] B、(0, ] C、(0,+∞) D、(﹣∞, ]2. 下列说法正确的是( )A、a∈R,“ <1”是“a>1”的必要不充分条件 B、“p∧q为真命题”是“p∨q为真命题”的必要不充分条件 C、命题“∃x∈R使得x2+2x+3<0”的否定是:“∀x∈R,x2+2x+3>0” D、命题p:“∀x∈R,sinx+cosx≤ ”,则¬p是真命题3. 已知点P(sinα﹣cosα,tanα)在第一象限,则在[0,2π]内α的取值范围是( )A、( , )∪(π, ) B、( , )∪(π, ) C、( , )∪( , ) D、( , )∪( ,π)4. 已知向量 =(x, ), =(x,﹣ ),若(2 + )⊥ ,则| |=( )A、1 B、 C、 D、25. 设f(x)= ,则 f(x)dx的值为( )A、 + B、 +3 C、 + D、 +36. 已知{an}是等差数列,a10=10,其前10项和S10=70,则其公差d=( )A、 B、 C、 D、7. 《九章算术》之后,人们进一步用等差数列求和公式来解决更多的问题,《张丘建算经》卷上第22题为:“今有女善织,日益功疾(注:从第2天开始,每天比前一天多织相同量的布),第一天织5尺布,现在一月(按30天计),共织390尺布”,则从第2天起每天比前一天多织( )尺布.A、 B、 C、 D、8. 函数y= 的定义域是( )A、[﹣ ,﹣1)∪(1, ] B、(﹣ ,﹣1)∪(1, ) C、[﹣2,﹣1)∪(1,2] D、(﹣2,﹣1)∪(1,2)9. 变量x、y满足条件 ,则(x﹣2)2+y2的最小值为( )A、 B、 C、 D、510. 函数y= 的图象大致为( )A、
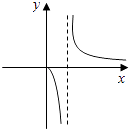 B、
B、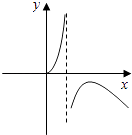 C、
C、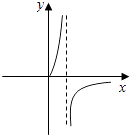 D、
D、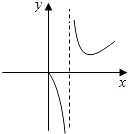 11. 已知函数y=f(x)是(﹣1,1)上的偶函数,且在区间(﹣1,0)上是单调递增的,A,B,C是锐角三角形△ABC的三个内角,则下列不等式中一定成立的是( )A、f(sinA)>f(sinB) B、f(sinA)>f(cosB) C、f(cosC)>f(sinB) D、f(sinC)>f(cosB)12. 若抛物线y2=2px(p>0)的焦点为F,其准线经过双曲线 的左焦点,点M为这两条曲线的一个交点,且|MF|=p,则双曲线的离心率为( )A、 B、 C、 D、
11. 已知函数y=f(x)是(﹣1,1)上的偶函数,且在区间(﹣1,0)上是单调递增的,A,B,C是锐角三角形△ABC的三个内角,则下列不等式中一定成立的是( )A、f(sinA)>f(sinB) B、f(sinA)>f(cosB) C、f(cosC)>f(sinB) D、f(sinC)>f(cosB)12. 若抛物线y2=2px(p>0)的焦点为F,其准线经过双曲线 的左焦点,点M为这两条曲线的一个交点,且|MF|=p,则双曲线的离心率为( )A、 B、 C、 D、二、填空题
-
13. 已知a= cosxdx,则x(x﹣ )7的展开式中的常数项是 . (用数字作答)14. 函数y=ex﹣mx在区间(0,3]上有两个零点,则m的取值范围是 .15. 已知函数f(x)=x3+3mx2+nx+m2在x=﹣1时有极值0,则m+n= .16. 将函数f(x)= sin(2x﹣ )+1的图象向左平移 个单位长度,再向下平移1个单位长度,得到函数g(x)的图象,则函数g(x)具有性质 . (填入所有正确性质的序号)
①最大值为 ,图象关于直线x= 对称;
②在(﹣ ,0)上单调递增,且为偶函数;
③最小正周期为π.
三、解答题
-
17. 已知p:x2﹣7x+10<0,q:x2﹣4mx+3m2<0,其中m>0.(1)、若m=4,且p∧q为真,求x的取值范围;(2)、若¬q是¬p的充分不必要条件,求实数m的取值范围.18. 在△ABC中,角A,B,C所对的边分别为a,b,c,且cos2 ﹣sinB•sinC= .(1)、求A;(2)、若a=4,求△ABC面积的最大值.19. 为及时了解适龄公务员对开放生育二胎政策的态度,某部门随机调查了90位30岁到40岁的公务员,得到情况如表:(1)、完成表格,并判断是否有99%以上的把握认为“生二胎意愿与性别有关”,并说明理由;(2)、现把以上频率当作概率,若从社会上随机独立抽取三位30岁到40岁的男公务员访问,求这三人中至少有一人有意愿生二胎的概率.(3)、已知15位有意愿生二胎的女性公务员中有两位来自省妇联,该部门打算从这15位有意愿生二胎的女性公务员中随机邀请两位来参加座谈,设邀请的2人中来自省女联的人数为X,求X的公布列及数学期望E(X).
男性公务员
女性公务员
总计
有意愿生二胎
30
15
无意愿生二胎
20
25
总计
附:
P(k2≥k0)
0.050
0.010
0.001
k0
3.841
6.635
10.828
20. 如图,直三棱柱ABC﹣A′B′C′中,AA′=2AC=2BC,E为AA′的中点,C′E⊥BE.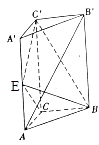 (1)、求证:C′E⊥平面BCE;(2)、求直线AB′与平面BEC′所成角的大小.21. 已知函数f(x)=ln(2ax+1)+ ﹣x2﹣2ax(a∈R).(1)、若x=2为f(x)的极值点,求实数a的值;(2)、若y=f(x)在[3,+∞)上为增函数,求实数a的取值范围;(3)、当a=﹣ 时,方程f(1﹣x)= 有实根,求实数b的最大值.
(1)、求证:C′E⊥平面BCE;(2)、求直线AB′与平面BEC′所成角的大小.21. 已知函数f(x)=ln(2ax+1)+ ﹣x2﹣2ax(a∈R).(1)、若x=2为f(x)的极值点,求实数a的值;(2)、若y=f(x)在[3,+∞)上为增函数,求实数a的取值范围;(3)、当a=﹣ 时,方程f(1﹣x)= 有实根,求实数b的最大值.