重庆110中2017-2018学年九年级上学期数学开学试卷

试卷更新日期：2018-07-27 类型：开学考试

进入出卷网下载

一、单选题

1. 下列汽车标志图案中既是轴对称图形也是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 如果把分式 $\frac{a b}{a + b}$ 中的a、b都扩大2倍，那么分式的值一定（）

A、是原来的2倍 B、是原来的4倍 C、是原来的 $\frac{1}{2}$ D、不变

查看试题解析
3. 要使分式 $\frac{4}{x - 3}$ 有意义，x应满足的条件是（）

A、x＞3 B、x=3 C、x＜3 D、x≠3

查看试题解析
4.
如图，▱ABCD的周长为20cm，AE平分∠BAD，若CE=2cm，则AB的长度是（　　）

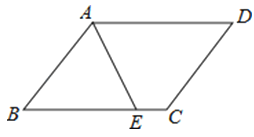A、10cm B、8cm C、6cm D、4cm

查看试题解析
5. 若一个多边形的每一个外角都是40°，则这个多边形是（　　）

A、六边形 B、八边形 C、九边形 D、十边形

查看试题解析
6. 若x>y，则下列式子中错误的是（）

A、x－3>y－3 B、 $\frac{x}{3} > \frac{y}{3}$ C、x+3>y+3 D、－3x>－3y

查看试题解析
7. 若m+n=3，则2m²+4mn+2n²﹣6的值为（）

A、12 B、6 C、3 D、0

查看试题解析
8. 下列各命题中，属于假命题的是（）

A、若a－b＝0，则a＝b＝0 B、若a－b＞0，则a＞b C、若a－b＜0，则a＜b D、若a－b≠0，则a≠b

查看试题解析
9. 若分式 $\frac{x^{2} - 1}{x - 1}$ 的值为零，则x的值是（）

A、±1 B、1 C、﹣1 D、0

查看试题解析
10. 如图所示，DE为△ABC的中位线，点F在DE上，且∠AFB=90°，若AB=6，BC=10，则EF的长为（）

A、1 B、2 C、3 D、5

查看试题解析
11. 下列图形都是由同样大小的菱形按照一定规律所组成的，其中第①个图形中一共有3个菱形，第②个图形中一共有7个菱形，第③个图形中一共有13个菱形，…，按此规律排列下去，第⑨个图形中菱形的个数为（）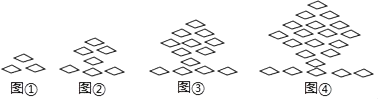

A、73 B、81 C、91 D、109

查看试题解析
12. 小敏是一位善于思考的学生，在一次数学活动课上，她将一副三角板按如图位置摆放，A，B，D在同一直线上，EF∥AD，∠BAC=∠EDF=90°，∠C=45°，∠E=60°，测得DE=8，则BD的长是（）

A、10+4 $\sqrt{3}$ B、10﹣4 $\sqrt{3}$ C、12﹣4 $\sqrt{3}$ D、12+4 $\sqrt{3}$

查看试题解析

二、填空题

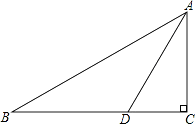
13. 不等式12﹣3x≥0的解集为．

查看试题解析
14. 分解因式：ax²-ay²= ．

查看试题解析
15. 如图，在△ABC中，∠C=90°，AB=10，AD是△ABC的一条角平分线．若CD=3，则△ABD的面积为．

查看试题解析
16. 若不等式组 ${\begin{matrix} x - a \geq 0 \\ 1 - 2 x > x - 2 \end{matrix}$ 恰有两个整数解，则a的取值范是．

查看试题解析
17. 如图，Rt△ABC中，∠ACB=90°，AC=3，BC=4，将△ABC绕点A逆时针旋转得到△AB′C′，AB′与BC相交于点D，当B′C′∥AB时，CD= ．

查看试题解析
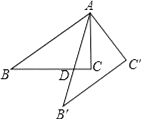18. 如图，矩形ABCD的边AB=1，BE平分∠ABC，交AD于点E，若点E是AD的中点，以点B为圆心，BE为半径画弧，交BC于点F，则图中阴影部分的面积是．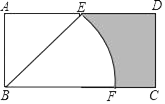

查看试题解析

三、解答题

19. 计算：

(1)、（2x﹣y）²﹣（x+y）（2x﹣y）

(2)、 $\frac{9 - a^{2}}{2 a^{2} - 4 a}$ ÷（ $\frac{5}{a - 2}$ ﹣a﹣2）．

查看试题解析
20.

(1)、解不等式组 ${\begin{matrix} x - 1 < 2 x \\ \frac{x}{2} + 2 \geq 3 (x - 1) \end{matrix}$

(2)、解方程 $\frac{1}{x + 2} + \frac{4 x}{x^{2} - 4} = \frac{2}{x - 2}$ ．

查看试题解析
21. 如图，在平行四边形ABCD中，E、F是AC上的两点，且AE=CF．求证：DE=BF．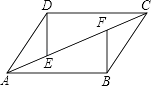

查看试题解析
22. 如图，在Rt△ABC中，∠ACB=90°，AC=4cm，BC=3cm，将△ABC沿AB方向向右平移得到△DEF，若AE=8cm．

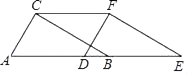(1)、求△ABC向右平移的距离AD的长；

(2)、求四边形AEFC的面积．

查看试题解析
23. 如图，在8×8的方格中建立平面直角坐标系，有点A（﹣2，2）、B（﹣3，1）、C（﹣1，0），P（a，b）是△ABC的AC边上点，将△ABC平移后得到△A₁B₁C₁ ，点P的对应点为P₁（a+4，b+2）．

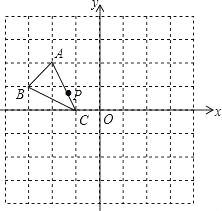(1)、画出平移后的△A₁B₁C₁ ，写出点A₁、C₁的坐标；

(2)、若以A、B、C、D为顶点的四边形为平行四边形，写出方格中D点的坐标．

查看试题解析
24. 某工厂，甲负责加工A型零件，乙负责加工B型零件．已知甲加工60个A型零件所用时间和乙加工80个B型零件所用时间相同，每天甲、乙两人共加工两种零件35个，设甲每天加工x个A型零件．

(1)、求甲、乙每天各加工多少个零件；

(2)、根据市场预测估计，加工一个A型零件所获得的利润为30元/件，加工一个B型零件所获得的利润每件比A型少5元．现在需要加工甲、乙两种零件共300个且要求所获得的总利润不低于8250元，求至少应生产多少个A型零件？

查看试题解析
25. 阅读下列材料：
解答“已知x﹣y=2，且x＞1，y＜0，试确定x+y的取值范围”有如下解法
解：∵x﹣y=2，∴x=y+2 又∵x＞1∴y+2＞1∴y＞﹣1
又∵y＜0∴﹣1＜y＜0…①
同理可得1＜x＜2…②
由①+②得：﹣1+1＜x+y＜0+2∴x+y的取值范围是0＜x+y＜2
按照上述方法，完成下列问题：

(1)、已知x﹣y=3，且x＞2，y＜1，则x+y的取值范围是

(2)、已知关于x，y的方程组 ${\begin{matrix} 3 x - y = 2 a - 5 \\ x + 2 y = 3 a + 3 \end{matrix}$ 的解都是正数
①求a的取值范围；②若a﹣b=4，求a+b的取值范围．

查看试题解析
26. 如图，已知△ABC，以AC为底边作等腰△ACD，且使∠ABC=2∠CAD，连接BD．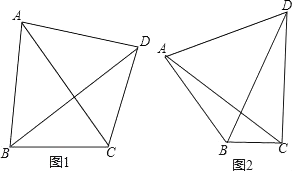

(1)、如图1，若∠ADC=90°，∠BAC=30°，BC=1，求CD的长；

(2)、如图1，若∠ADC=90°，证明：AB+BC= $\sqrt{2}$ BD；

(3)、如图2，若∠ADC=60°，探究AB，BC，BD之间的数量关系并证明．

查看试题解析