江西省吉安八中2015-2016学年八年级上学期数学开学考试试卷
试卷更新日期：2018-07-27 类型：开学考试
一、单选题
-
1. PM2.5是大气中直径小于或等于0.0000025m的颗粒物，它能较长时间悬浮于空气中，其在空气中含量浓度越高，就代表空气污染越严重．请将0.0000025用科学记数法表示为（ ）A、0.25×10﹣5 B、25×10﹣7 C、2.5×10﹣6 D、2.5×10﹣52. 从长为10cm、7cm、5cm、3cm的四条线段中任选三条能够组成三角形的概率是（ ）A、 B、 C、 D、3.
如图所示的矩形纸片，先沿虚线按箭头方向向右对折，接着将对折后的纸片沿虚线剪下一个小圆和一个小三角形，然后将纸片打开是下列图中的哪一个（ ）
A、
B、
C、
D、
4. 下列图形中，由AB∥CD，能使∠1=∠2成立的是（ ）A、
B、
C、
D、
5. 在下列的计算中，正确的是（ ）A、2x+3y=5xy B、（a+2）（a﹣2）=a2+4 C、a2•ab=a3b D、（x﹣3）2=x2+6x+96. 等腰三角形的周长为30cm，其中一边长12cm，则其腰长为（ ）A、9cm B、12cm或9cm C、10cm或9cm D、以上都不对7. 如图1，在矩形MNPQ中，动点R从点N出发，沿N→P→Q→M方向运动至点M处停止．设点R运动的路程为x，△MNR的面积为y，如果y关于x的函数图象如图2所示，则当x=9时，点R应运动到（ ）
A、N处 B、P处 C、Q处 D、M处二、填空题
-
8. 计算：（4x3y2﹣2xy）÷2xy= ．9. 如图，AB∥CD，EF⊥AB于E，EF交CD于F，已知∠1=60°，则∠2= ．
10. 如图，把一个长方形纸片沿EF折叠后，点D、C分别落在D′、C′的位置．若∠EFB=65°，则∠AED′等于°．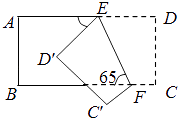
11. 在科学课外活动中，小明同学在相同的条件下做了某种作物种子发芽实验，结果如下表所示：
由此估计这种作物种子的发芽率为.
12. 如图，在Rt△ABC中，∠A=90°，∠ABC的平分线BD交AC于点D，AD=3，BC=10，则△BDC的面积是 ．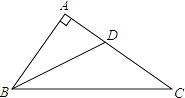
13. 如图，点P是∠AOB的角平分线OC上一点，分别连接AP、BP，若再添加一个条件即可判定△AOP≌△BPO，则一下条件中：①∠A=∠B；②∠APO=∠BPO；③∠APC=∠BPC； ④AP=BP；⑤OA=OB．其中一定正确的是（只需填序号即可）
三、解答题
-
14. 计算：(1)、(2)、（x+2y）2﹣（3x+y）（x+2y）(3)、[（2a+b）2﹣（2a﹣b）2+6b2]÷2b(4)、[（xy+2）（xy﹣2）﹣2x2y2+4]÷xy，其中x=10，y=﹣ ．15. 在如图所示的正方形网格中，已知△ABC的三个顶点分别是格点A ， B ， C ．
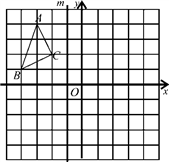(1)、请在正方形网格中作△A1B1C1 ， 使它与△ABC关于直线m成轴对称，其中点A1 ， B1 ， C1分别是A ， B ， C的对称点．(2)、若网格中小正方形的边长为1，求四边形BCC1B1的面积．16. 一个不透明的袋中装有红、黄、白三种颜色球共100个，它们除颜色外都相同，其中黄球个数是白球个数的2倍少5个．已知从袋中摸出一个球是红球的概率是 ．(1)、求袋中红球的个数；(2)、求从袋中摸出一个球是白球的概率；(3)、取走10个球（其中没有红球）后，求从剩余的球中摸出一个球是红球的概率．17. 如图，△ABC是等边三角形，D是AB边上一点，以CD为边作等边△CDE，使点E、A在直线DC的同侧，连接AE，判断AE与BC的位置关系，并说明理由．
18. 某移动通讯公司开设了两种通讯业务：“全球通”使用者先缴50元月租费，然后每通话1分钟，再付话费0.4元；“神州行”不缴月租费，每通话1 min付费0.6元．若一个月内通话x min，两种方式的费用分别为y1元和y2元．(1)、写出y1 ， y2与x之间的函数解析式；(2)、一个月内通话多少分钟，两种通讯业务费用相同；(3)、某人估计一个月内通话300 min，应选择哪种移动通讯业务合算些？19. 以点A为顶点作等腰Rt△ABC，等腰Rt△ADE，其中∠BAC=∠DAE=90°，如图1所示放置，使得一直角边重合，连接BD、CE．
(1)、试判断BD、CE的数量关系，并说明理由；(2)、延长BD交CE于点F试求∠BFC的度数；(3)、把两个等腰直角三角形按如图2放置，（1）、（2）中的结论是否仍成立？请说明理由．