内蒙古通辽市2018年中考数学试卷
试卷更新日期:2018-07-27 类型:中考真卷
一、选择题
-
1. 的倒数是( )A、2018 B、﹣2018 C、﹣ D、2. 剪纸是我国传统的民间艺术,下列剪纸作品中既不是轴对称图形,也不是中心对称图形的是( )
A、 B、
B、 C、
C、 D、
D、 3. 下列说法错误的是( )A、通过平移或旋转得到的图形与原图形全等 B、“对顶角相等”的逆命题是真命题 C、圆内接正六边形的边长等于半径 D、“经过有交通信号灯的路口,遇到红灯”是随机事件4. 小刚从家去学校,先匀速步行到车站,等了几分钟后坐上了公交车,公交车匀速行驶一段时后到达学校,小刚从家到学校行驶路程s(单位:m)与时间r(单位:min)之间函数关系的大致图象是( )A、
3. 下列说法错误的是( )A、通过平移或旋转得到的图形与原图形全等 B、“对顶角相等”的逆命题是真命题 C、圆内接正六边形的边长等于半径 D、“经过有交通信号灯的路口,遇到红灯”是随机事件4. 小刚从家去学校,先匀速步行到车站,等了几分钟后坐上了公交车,公交车匀速行驶一段时后到达学校,小刚从家到学校行驶路程s(单位:m)与时间r(单位:min)之间函数关系的大致图象是( )A、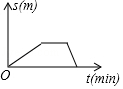 B、
B、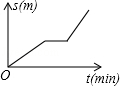 C、
C、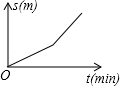 D、
D、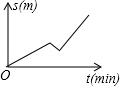 5. 如图,一个几何体的主视图和左视图都是边长为6的等边三角形,俯视图是直径为6的圆,则此几何体的全面积是( )
5. 如图,一个几何体的主视图和左视图都是边长为6的等边三角形,俯视图是直径为6的圆,则此几何体的全面积是( )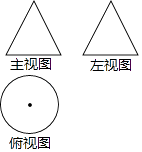 A、18π B、24π C、27π D、42π6. 学校为创建“书香校园”购买了一批图书.已知购买科普类图书花费10000元,购买文学类图书花费9000元,其中科普类图书平均每本的价格比文学类图书平均每本的价格贵5元,且购买科普书的数量比购买文学书的数量少100本.求科普类图书平均每本的价格是多少元?若设科普类图书平均每本的价格是x元,则可列方程为( )
A、18π B、24π C、27π D、42π6. 学校为创建“书香校园”购买了一批图书.已知购买科普类图书花费10000元,购买文学类图书花费9000元,其中科普类图书平均每本的价格比文学类图书平均每本的价格贵5元,且购买科普书的数量比购买文学书的数量少100本.求科普类图书平均每本的价格是多少元?若设科普类图书平均每本的价格是x元,则可列方程为( )
A、 ﹣ =100 B、 ﹣ =100 C、 ﹣ =100 D、 ﹣ =1007. 已知⊙O的半径为10,圆心O到弦AB的距离为5,则弦AB所对的圆周角的度数是( )
A、30° B、60° C、30°或150° D、60°或120°8. 一商店以每件150元的价格卖出两件不同的商品,其中一件盈利25%,另一件亏损25%,则商店卖这两件商品总的盈亏情况是( )
A、亏损20元 B、盈利30元 C、亏损50元 D、不盈不亏9. 已知抛物线y=x2+2x+k+1与x轴有两个不同的交点,则一次函数y=kx﹣k与反比例函数y= 在同一坐标系内的大致图象是( )
A、 B、
B、 C、
C、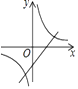 D、
D、 10. 如图,▱ABCD的对角线AC、BD交于点O,DE平分∠ADC交AB于点E,∠BCD=60°,AD= AB,连接OE.下列结论:①S▱ABCD=AD•BD;②DB平分∠CDE;③AO=DE;④S△ADE=5S△OFE , 其中正确的个数有( )
10. 如图,▱ABCD的对角线AC、BD交于点O,DE平分∠ADC交AB于点E,∠BCD=60°,AD= AB,连接OE.下列结论:①S▱ABCD=AD•BD;②DB平分∠CDE;③AO=DE;④S△ADE=5S△OFE , 其中正确的个数有( )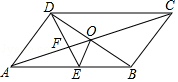 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 2018年5月13日,我国第一艘国产航母出海试航,这标志着我国从此进入“双航母”时代,据估测该航母的满载排水量与辽宁舰相当,约67500吨,将67500用科学记数法表示为 .12. 如图,∠AOB的一边OA为平面镜,∠AOB=37°45′,在OB边上有一点E,从点E射出一束光线经平面镜反射后,反射光线DC恰好与OB平行,则∠DEB的度数是 .
 13. 一组数据2,x,1,3,5,4,若这组数据的中位数是3,则这组数据的方差是 .
13. 一组数据2,x,1,3,5,4,若这组数据的中位数是3,则这组数据的方差是 .
14. 如图,这个图案是3世纪我国汉代数学家赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”.已知AE=3,BE=2,若向正方形ABCD内随意投掷飞镖(每次均落在正方形ABCD内,且落在正方形ABCD内任何一点的机会均等),则恰好落在正方形EFGH内的概率为 . 15. 为增强学生身体素质,提高学生足球运动竞技水平,我市开展“市长杯”足球比赛,赛制为单循环形式(每两队之间赛一场).现计划安排21场比赛,应邀请多少个球队参赛?设邀请x个球队参赛,根据题意,可列方程为 .
15. 为增强学生身体素质,提高学生足球运动竞技水平,我市开展“市长杯”足球比赛,赛制为单循环形式(每两队之间赛一场).现计划安排21场比赛,应邀请多少个球队参赛?设邀请x个球队参赛,根据题意,可列方程为 .
16. 如图,在△ABC中,按以下步骤作图:①分别以点A和点C为圆心,以大于 AC的长为半径作弧,两弧相交于M、N两点;②作直线MN交BC于点D,连接AD.若AB=BD,AB=6,∠C=30°,则△ACD的面积为 .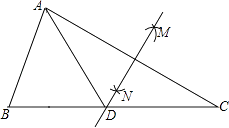 17. 如图,在平面直角坐标系中,反比例函数y= (k>0)的图象与半径为5的⊙O交于M、N两点,△MON的面积为3.5,若动点P在x轴上,则PM+PN的最小值是 .
17. 如图,在平面直角坐标系中,反比例函数y= (k>0)的图象与半径为5的⊙O交于M、N两点,△MON的面积为3.5,若动点P在x轴上,则PM+PN的最小值是 .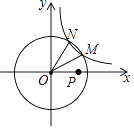
三、解答题
-
18. 计算:﹣|4﹣ |﹣(π﹣3.14)0+(1﹣cos30°)×( )﹣2 .
19. 先化简(1﹣ )÷ ,然后从不等式2x﹣6<0的非负整数解中选取一个合适的解代入求值.
20. 我市304国道通辽至霍林郭勒段在修建过程中经过一座山峰,如图所示,其中山脚A、C两地海拔高度约为1000米,山顶B处的海拔高度约为1400米,由B处望山脚A处的俯角为30°,由B处望山脚C处的俯角为45°,若在A、C两地间打通一隧道,求隧道最短为多少米(结果取整数,参考数据 ≈1.732)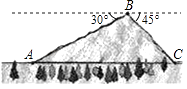 21. 为了解某校九年级学生立定跳远水平,随机抽取该年级50名学生进行测试,并把测试成绩(单位:m)绘制成不完整的频数分布表和频数分布直方图.
21. 为了解某校九年级学生立定跳远水平,随机抽取该年级50名学生进行测试,并把测试成绩(单位:m)绘制成不完整的频数分布表和频数分布直方图.学生立定跳远测试成绩的频数分布表
分组
频数
1.2≤x<1.6
a
1.6≤x<2.0
12
2.0≤x<2.4
b
2.4≤x<2.8
10
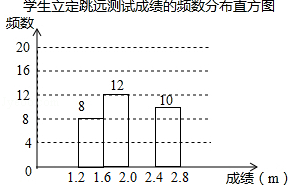
请根据图表中所提供的信息,完成下列问题:
(1)、表中a= , b= , 样本成绩的中位数落在范围内;
(2)、请把频数分布直方图补充完整;(3)、该校九年级共有1000名学生,估计该年级学生立定跳远成绩在2.4≤x<2.8范围内的学生有多少人?22. 如图,△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交BE的延长线于F,且AF=CD,连接CF. (1)、求证:△AEF≌△DEB;(2)、若AB=AC,试判断四边形ADCF的形状,并证明你的结论.23. 为提升学生的艺术素养,学校计划开设四门艺术选修课:A.书法;B.绘画;C.乐器;D.舞蹈.为了解学生对四门功课的喜欢情况,在全校范围内随机抽取若干名学生进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门).将数据进行整理,并绘制成如下两幅不完整的统计图,请结合图中所给信息解答下列问题:
(1)、求证:△AEF≌△DEB;(2)、若AB=AC,试判断四边形ADCF的形状,并证明你的结论.23. 为提升学生的艺术素养,学校计划开设四门艺术选修课:A.书法;B.绘画;C.乐器;D.舞蹈.为了解学生对四门功课的喜欢情况,在全校范围内随机抽取若干名学生进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门).将数据进行整理,并绘制成如下两幅不完整的统计图,请结合图中所给信息解答下列问题: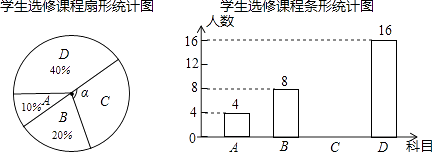 (1)、本次调查的学生共有多少人?扇形统计图中∠α的度数是多少?
(1)、本次调查的学生共有多少人?扇形统计图中∠α的度数是多少?
(2)、请把条形统计图补充完整;(3)、学校为举办2018年度校园文化艺术节,决定从A.书法;B.绘画;C.乐器;D.舞蹈四项艺术形式中选择其中两项组成一个新的节目形式,请用列表法或树状图求出选中书法与乐器组合在一起的概率.
24. 某网店销售甲、乙两种羽毛球,已知甲种羽毛球每筒的售价比乙种羽毛球多15元,王老师从该网店购买了2筒甲种羽毛球和3筒乙种羽毛球,共花费255元.
(1)、该网店甲、乙两种羽毛球每筒的售价各是多少元?(2)、根据消费者需求,该网店决定用不超过8780元购进甲、乙两种羽毛球共200筒,且甲种羽毛球的数量大于乙种羽毛球数量的 ,已知甲种羽毛球每筒的进价为50元,乙种羽毛球每筒的进价为40元.①若设购进甲种羽毛球m筒,则该网店有哪几种进货方案?
②若所购进羽毛球均可全部售出,请求出网店所获利润W(元)与甲种羽毛球进货量m(筒)之间的函数关系式,并说明当m为何值时所获利润最大?最大利润是多少?
25. 如图,⊙O是△ABC的外接圆,点O在BC边上,∠BAC的平分线交⊙O于点D,连接BD、CD,过点D作BC的平行线与AC的延长线相交于点P.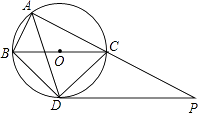 (1)、求证:PD是⊙O的切线;
(1)、求证:PD是⊙O的切线;
(2)、求证:△ABD∽△DCP;
(3)、当AB=5cm,AC=12cm时,求线段PC的长.
26. 如图,抛物线y=ax2+bx﹣5与坐标轴交于A(﹣1,0),B(5,0),C(0,﹣5)三点,顶点为D.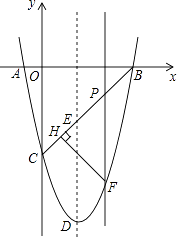 (1)、请直接写出抛物线的解析式及顶点D的坐标;(2)、连接BC与抛物线的对称轴交于点E,点P为线段BC上的一个动点(点P不与B、C两点重合),过点P作PF∥DE交抛物线于点F,设点P的横坐标为m.
(1)、请直接写出抛物线的解析式及顶点D的坐标;(2)、连接BC与抛物线的对称轴交于点E,点P为线段BC上的一个动点(点P不与B、C两点重合),过点P作PF∥DE交抛物线于点F,设点P的横坐标为m.①是否存在点P,使四边形PEDF为平行四边形?若存在,求出点P的坐标;若不存在,说明理由.
②过点F作FH⊥BC于点H,求△PFH周长的最大值.