湖北省咸宁市2018年中考数学试卷

试卷更新日期：2018-07-27 类型：中考真卷

进入出卷网下载

一、选择题

1. 咸宁冬季里某一天的气温为﹣3℃～2℃，则这一天的温差是（）

A、1℃ B、﹣1℃ C、5℃ D、﹣5℃

查看试题解析
2. 如图，已知a∥b，l与a、b相交，若∠1=70°，则∠2的度数等于（）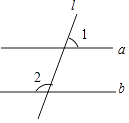

A、120° B、110° C、100° D、70°

查看试题解析
3. 2017年，咸宁市经济运行总体保持平稳较快增长，全年GDP约123500000000元，增速在全省17个市州中排名第三，将123500000000用科学记数法表示为（）

A、 123.5×10⁹ B、12.35×10¹⁰ C、1.235×10⁸ D、1.235×10¹¹

查看试题解析
4. 用4个完全相同的小正方体搭成如图所示的几何体，该几何体的（）

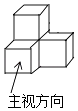A、主视图和左视图相同 B、主视图和俯视图相同 C、左视图和俯视图相同 D、三种视图都相同

查看试题解析
5. 下列计算正确的是（）

A、a³•a³=2a³ B、a²+a²=a⁴ C、a⁶÷a²=a³ D、（﹣2a²）³=﹣8a⁶

查看试题解析
6. 已知一元二次方程2x²+2x﹣1=0的两个根为x₁ ， x₂ ，且x₁＜x₂ ，下列结论正确的是（）

A、x₁+x₂=1 B、x₁•x₂=﹣1 C、|x₁|＜|x₂| D、x₁²+x₁= $\frac{1}{2}$

查看试题解析
7. 如图，已知⊙O的半径为5，弦AB，CD所对的圆心角分别是∠AOB，COD，若∠AOB与∠COD互补，弦CD=6，则弦AB的长为（）

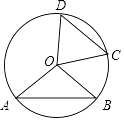A、6 B、8 C、5 $\sqrt{2}$ D、5 $\sqrt{3}$

查看试题解析
8. 甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米，先到终点的人原地休息．已知甲先出发4分钟，在整个步行过程中，甲、乙两人的距离y（米）与甲出发的时间t（分）之间的关系如图所示，下列结论：①甲步行的速度为60米/分；②乙走完全程用了32分钟；③乙用16分钟追上甲；④乙到达终点时，甲离终点还有300米其中正确的结论有（）

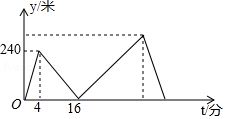A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

9. 如果分式 $\frac{1}{x - 2}$ 有意义，那么实数x的取值范围是．

查看试题解析
10. 因式分解：ab²﹣a= ．

查看试题解析
11. 写出一个比2大比3小的无理数（用含根号的式子表示）．

查看试题解析
12. 一个不透明的口袋中有三个完全相同的小球，把它们分别标号为1，2，3.随机摸出一个小球然后放回，再随机摸出一个小球，则两次摸出的小球标号相同的概率是．

查看试题解析
13. 如图，航拍无人机从A处测得一幢建筑物顶部B的仰角为45°，测得底部C的俯角为60°，此时航拍无人机与该建筑物的水平距离AD为110m，那么该建筑物的高度BC约为m（结果保留整数， $\sqrt{3}$ ≈1.73）．

查看试题解析
14. 如图，将正方形OEFG放在平面直角坐标系中，O是坐标原点，点E的坐标为（2，3），则点F的坐标为．

查看试题解析
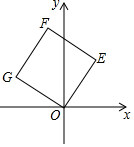15. 按一定顺序排列的一列数叫做数列，如数列： $\frac{1}{2}$ ， $\frac{1}{6}$ ， $\frac{1}{12}$ ， $\frac{1}{20}$ ，…，则这个数列前2018个数的和为．

查看试题解析
16. 如图，已知∠MON=120°，点A，B分别在OM，ON上，且OA=OB=a，将射线OM绕点O逆时针旋转得到OM′，旋转角为α（0°＜α＜120°且α≠60°），作点A关于直线OM′的对称点C，画直线BC交OM′于点D，连接AC，AD，有下列结论：①AD=CD；②∠ACD的大小随着α的变化而变化；③当α=30°时，四边形OADC为菱形；④△ACD面积的最大值为 $\sqrt{3}$ a²；其中正确的是．（把你认为正确结论的序号都填上）．

查看试题解析

三、解答题

17.

(1)、计算： $\sqrt{12} - \sqrt[3]{8}$ +| $\sqrt{3}$ ﹣2|；

(2)、化简：（a+3）（a﹣2）﹣a（a﹣1）．

查看试题解析
18. 已知：∠AOB．
求作：∠A'O'B'，使∠A'O′B'=∠AOB
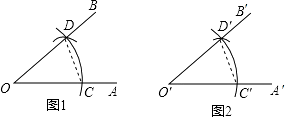
①如图1，以点O为圆心，任意长为半径画弧，分别交OA，OB于点C、D；
②如图2，画一条射线O′A′，以点O′为圆心，OC长为半径画弧，交O′A′于点C′；
③以点C′为圆心，CD长为半径画弧，与第2步中所而的弧交于点D′；
④过点D′画射线O′B'，则∠A'O'B'=∠AOB．
根据以上作图步骤，请你证明∠A'O'B′=∠AOB．

查看试题解析
19. 近年来，共享单车逐渐成为高校学生喜爱的“绿色出行”方式之一，自2016年国庆后，许多高校均投放了使用手机支付就可随取随用的共享单车．某高校为了解本校学生出行使用共享单车的情况，随机调查了某天部分出行学生使用共享单车的情况，并整理成如下统计表．
使用次数
0
1
2
3
4
5
人数
11
15
23
28
18
5

(1)、这天部分出行学生使用共享单车次数的中位数是，众数是，该中位数的意义是；

(2)、这天部分出行学生平均每人使用共享单车约多少次？（结果保留整数）

(3)、若该校某天有1500名学生出行，请你估计这天使用共享单车次数在3次以上（含3次）的学生有多少人？

查看试题解析
20. 如图，在平面直角坐标系中，矩形OABC的顶点B的坐标为（4，2），直线y=﹣ $\frac{1}{2}$ x+ $\frac{5}{2}$ 与边AB，BC分别相交于点M，N，函数y= $\frac{k}{x}$ （x＞0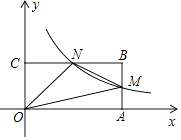）的图象过点M．

(1)、试说明点N也在函数y= $\frac{k}{x}$ （x＞0）的图象上；

(2)、将直线MN沿y轴的负方向平移得到直线M′N′，当直线M′N′与函数y═ $\frac{k}{x}$ （x＞0）的图象仅有一个交点时，求直线M'N′的解析式．

查看试题解析
21. 如图，以△ABC的边AC为直径的⊙O恰为△ABC的外接圆，∠ABC的平分线交⊙O于点D，过点D作DE∥AC交BC的延长线于点E．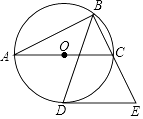

(1)、求证：DE是⊙O的切线；

(2)、若AB=25，BC= $\sqrt{5}$ ，求DE的长．

查看试题解析
22. 为拓宽学生视野，引导学生主动适应社会，促进书本知识和生活经验的深度融合，我市某中学决定组织部分班级去赤壁开展研学旅行活动，在参加此次活动的师生中，若每位老师带17个学生，还剩12个学生没人带；若每位老师带18个学生，就有一位老师少带4个学生．现有甲、乙两种大客车，它们的载客量和租金如表所示．

甲种客车
乙种客车
载客量/（人/辆）
30
42
租金/（元/辆）
300
400
学校计划此次研学旅行活动的租车总费用不超过3100元，为了安全，每辆客车上至少要有2名老师．

(1)、参加此次研学旅行活动的老师和学生各有多少人？

(2)、既要保证所有师生都有车坐，又要保证每辆客车上至少要有2名老师，可知租用客车总数为辆；

(3)、你能得出哪几种不同的租车方案？其中哪种租车方案最省钱？请说明理由．

查看试题解析
23. 定义：
我们知道，四边形的一条对角线把这个四边形分成了两个三角形，如果这两个三角形相似（不全等），我们就把这条对角线叫做这个四边形的“相似对角线”．
理解：

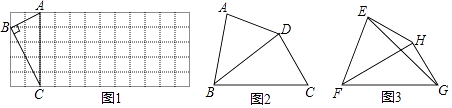(1)、如图1，已知Rt△ABC在正方形网格中，请你只用无刻度的直尺在网格中找到一点D，使四边形ABCD是以AC为“相似对角线”的四边形（保留画图痕迹，找出3个即可）；

(2)、如图2，在四边形ABCD中，∠ABC=80°，∠ADC=140°，对角线BD平分∠ABC．
求证：BD是四边形ABCD的“相似对角线”；

(3)、如图3，已知FH是四边形EFCH的“相似对角线”，∠EFH=∠HFG=30°，连接EG，若△EFG的面积为2 $\sqrt{3}$ ，求FH的长．

查看试题解析
24. 如图，直线y=﹣ $\frac{3}{4}$ x+3与x轴交于点A，与y轴交于点B．抛物线y=﹣ $\frac{3}{8}$ x²+bx+c经过A、B两点，与x轴的另一个交点为C．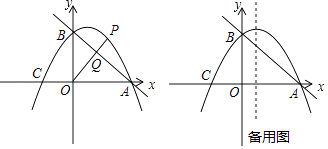

(1)、求抛物线的解析式；

(2)、点P是第一象限抛物线上的点，连接OP交直线AB于点Q．设点P的横坐标为m，PQ与OQ的比值为y，求y与m的数关系式，并求出PQ与OQ的比值的最大值；

(3)、点D是抛物线对称轴上的一动点，连接OD、CD，设△ODC外接圆的圆心为M，当sin∠ODC的值最大时，求点M的坐标．

查看试题解析

	甲种客车	乙种客车
载客量/（人/辆）	30	42
租金/（元/辆）	300	400

使用次数	0	1	2	3	4	5
人数	11	15	23	28	18	5