广西壮族自治区贵港市2018年中考数学试卷
试卷更新日期：2018-07-27 类型：中考真卷
一、选择题
-
1. 的倒数是（ ）A、8 B、 C、 D、2. 一条数学信息在一周内被转发了2180000次，将数据2180000用科学记数法表示为（ ）A、2.18×106 B、2.18×105 C、21.8×106 D、21.8×1053. 下列运算正确的是（ ）A、2a﹣a=1 B、2a+b=2ab C、（a4）3=a7 D、（﹣a）2•（﹣a）3=﹣a54. 笔筒中有10支型号、颜色完全相同的铅笔，将它们逐一标上1﹣10的号码，若从笔筒中任意抽出一支铅笔，则抽到编号是3的倍数的概率是（ ）
A、 B、 C、 D、5. 若点A（1+m，1﹣n）与点B（﹣3，2）关于y轴对称，则m+n的值是（ ）A、﹣5 B、﹣3 C、3 D、16. 已知α，β是一元二次方程x2+x﹣2=0的两个实数根，则α+β﹣αβ的值是（ ）A、3 B、1 C、﹣1 D、﹣37. 若关于x的不等式组 无解，则a的取值范围是（ ）A、a≤﹣3 B、a＜﹣3 C、a＞3 D、a≥38. 下列命题中真命题是（ ）A、 =（ ）2一定成立 B、位似图形不可能全等 C、正多边形都是轴对称图形 D、圆锥的主视图一定是等边三角形9. 如图，点A，B，C均在⊙O上，若∠A=66°，则∠OCB的度数是（ ）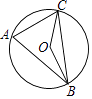
A、24° B、28° C、33° D、48°10. 如图，在△ABC中，EF∥BC，AB=3AE，若S四边形BCFE=16，则S△ABC=（ ）
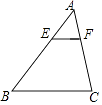A、16 B、18 C、20 D、2411. 如图，在菱形ABCD中，AC=6 ，BD=6，E是BC边的中点，P，M分别是AC，AB上的动点，连接PE，PM，则PE+PM的最小值是（ ）
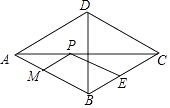A、6 B、3 C、2 D、4.512. 如图，抛物线y= （x+2）（x﹣8）与x轴交于A，B两点，与y轴交于点C，顶点为M，以AB为直径作⊙D．下列结论：①抛物线的对称轴是直线x=3；②⊙D的面积为16π；③抛物线上存在点E，使四边形ACED为平行四边形；④直线CM与⊙D相切．其中正确结论的个数是（ ）
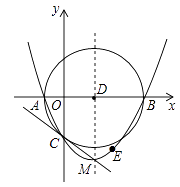A、1 B、2 C、3 D、4二、填空题
-
13. 若分式 的值不存在，则x的值为 ．14. 因式分解：ax2﹣a= ．15. 已知一组数据4，x，5，y，7，9的平均数为6，众数为5，则这组数据的中位数是 ．16. 如图，将矩形ABCD折叠，折痕为EF，BC的对应边B'C′与CD交于点M，若∠B′MD=50°，则∠BEF的度数为 ．
17. 如图，在Rt△ABC中，∠ACB=90°，AB=4，BC=2，将△ABC绕点B顺时针方向旋转到△A′BC′的位置，此时点A′恰好在CB的延长线上，则图中阴影部分的面积为（结果保留π）．
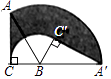18. 如图，直线l为y= x，过点A1（1，0）作A1B1⊥x轴，与直线l交于点B1 ， 以原点O为圆心，OB1长为半径画圆弧交x轴于点A2；再作A2B2⊥x轴，交直线l于点B2 ， 以原点O为圆心，OB2长为半径画圆弧交x轴于点A3；……，按此作法进行下去，则点An的坐标为（）．
三、解答题
-
19.
(1)、计算：|3﹣5|﹣（π﹣3.14）0+（﹣2）﹣1+sin30°；(2)、解分式方程： +1= ．20. 尺规作图（只保留作图痕迹，不要求写出作法）．如图，已知∠α和线段a，求作△ABC，使∠A=∠α，∠C=90°，AB=a．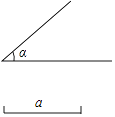
21. 如图，已知反比例函数y= （x＞0）的图象与一次函数y=﹣ x+4的图象交于A和B（6，n）两点．
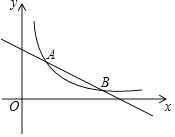(1)、求k和n的值；
(2)、若点C（x，y）也在反比例函数y= （x＞0）的图象上，求当2≤x≤6时，函数值y的取值范围．22. 为了增强学生的环保意识，某校组织了一次全校2000名学生都参加的“环保知识”考试，考题共10题．考试结束后，学校团委随机抽查部分考生的考卷，对考生答题情况进行分析统计，发现所抽查的考卷中答对题量最少为6题，并且绘制了如下两幅不完整的统计图．请根据统计图提供的信息解答以下问题：
(1)、本次抽查的样本容量是；在扇形统计图中，m= ， n= ， “答对8题”所对应扇形的圆心角为度；(2)、将条形统计图补充完整；(3)、请根据以上调查结果，估算出该校答对不少于8题的学生人数．
23. 某中学组织一批学生开展社会实践活动，原计划租用45座客车若干辆，但有15人没有座位；若租用同样数量的60座客车，则多出一辆车，且其余客车恰好坐满.已知45座客车租金为每辆220元，60座客车租金为每辆300元，问：(1)、这批学生的人数是多少？原计划租用45座客车多少辆？；
(2)、若租用同一种车，要使每位学生都有座位，应该怎样租用才合算？24. 如图，已知⊙O是△ABC的外接圆，且AB=BC=CD，AB∥CD，连接BD．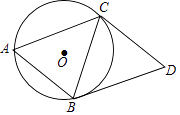
(1)、求证：BD是⊙O的切线；
(2)、若AB=10，cos∠BAC= ，求BD的长及⊙O的半径．25. 如图，已知二次函数y=ax2+bx+c的图象与x轴相交于A（﹣1，0），B（3，0）两点，与y轴相交于点C（0，﹣3）．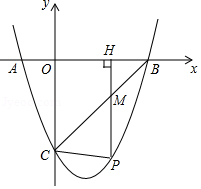
(1)、求这个二次函数的表达式；
(2)、若P是第四象限内这个二次函数的图象上任意一点，PH⊥x轴于点H，与BC交于点M，连接PC．①求线段PM的最大值；
②当△PCM是以PM为一腰的等腰三角形时，求点P的坐标．
26. 已知：A、B两点在直线l的同一侧，线段AO，BM均是直线l的垂线段，且BM在AO的右边，AO=2BM，将BM沿直线l向右平移，在平移过程中，始终保持∠ABP=90°不变，BP边与直线l相交于点P．
(1)、当P与O重合时（如图2所示），设点C是AO的中点，连接BC．求证：四边形OCBM是正方形；(2)、请利用如图1所示的情形，求证： = ；(3)、若AO=2 ，且当MO=2PO时，请直接写出AB和PB的长．