黑龙江省大庆市2018年中考数学试卷
试卷更新日期:2018-07-26 类型:中考真卷
一、选择题
-
1. 2cos60°=( )A、1 B、 C、 D、2. 一种花粉颗粒直径约为0.0000065米,数字0.0000065用科学记数法表示为( )A、0.65×10﹣5 B、65×10﹣7 C、6.5×10﹣6 D、6.5×10﹣53. 已知两个有理数a,b,如果ab<0且a+b>0,那么( )A、a>0,b>0 B、a<0,b>0 C、a、b同号 D、a、b异号,且正数的绝对值较大4. 一个正n边形的每一个外角都是36°,则n=( )A、7 B、8 C、9 D、105. 某商品打七折后价格为a元,则原价为( )A、a元 B、 a元 C、30%a元 D、 a元6. 将正方体的表面沿某些棱剪开,展成如图所示的平面图形,则原正方体中与“创”字所在的面相对的面上标的字是( )
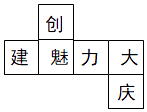 A、庆 B、力 C、大 D、魅7. 在同一直角坐标系中,函数y= 和y=kx﹣3的图象大致是( )A、
A、庆 B、力 C、大 D、魅7. 在同一直角坐标系中,函数y= 和y=kx﹣3的图象大致是( )A、 B、
B、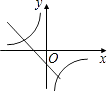 C、
C、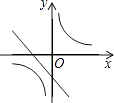 D、
D、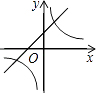 8. 已知一组数据:92,94,98,91,95的中位数为a,方差为b,则a+b=( )A、98 B、99 C、100 D、1029. 如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC,且∠ADC=110°,则∠MAB=( )
8. 已知一组数据:92,94,98,91,95的中位数为a,方差为b,则a+b=( )A、98 B、99 C、100 D、1029. 如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC,且∠ADC=110°,则∠MAB=( )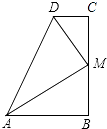 A、30° B、35° C、45° D、60°10. 如图,二次函数y=ax2+bx+c的图象经过点A(﹣1,0)、点B(3,0)、点C(4,y1),若点D(x2 , y2)是抛物线上任意一点,有下列结论:①二次函数y=ax2+bx+c的最小值为﹣4a;②若﹣1≤x2≤4,则0≤y2≤5a;③若y2>y1 , 则x2>4;④一元二次方程cx2+bx+a=0的两个根为﹣1和 其中正确结论的个数是( )
A、30° B、35° C、45° D、60°10. 如图,二次函数y=ax2+bx+c的图象经过点A(﹣1,0)、点B(3,0)、点C(4,y1),若点D(x2 , y2)是抛物线上任意一点,有下列结论:①二次函数y=ax2+bx+c的最小值为﹣4a;②若﹣1≤x2≤4,则0≤y2≤5a;③若y2>y1 , 则x2>4;④一元二次方程cx2+bx+a=0的两个根为﹣1和 其中正确结论的个数是( )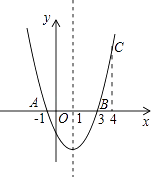 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
11. 已知圆柱的底面积为60cm2 , 高为4cm,则这个圆柱体积为cm3 .12. 函数y= 的自变量x取值范围是 .13. 在平面直角坐标系中,点A的坐标为(a,3),点B的坐标是(4,b),若点A与点B关于原点O对称,则ab= .14. 在△ABC中,∠C=90°,AB=10,且AC=6,则这个三角形的内切圆半径为 .15. 若2x=5,2y=3,则22x+y= .16. 已知 = + ,则实数A= .17. 如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,将Rt△ABC绕点A逆时针旋转30°后得到Rt△ADE,点B经过的路径为弧BD,则图中阴影部分的面积为 .
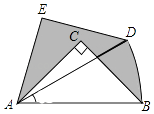 18. 已知直线y=kx(k≠0)经过点(12,﹣5),将直线向上平移m(m>0)个单位,若平移后得到的直线与半径为6的⊙O相交(点O为坐标原点),则m的取值范围为 .
18. 已知直线y=kx(k≠0)经过点(12,﹣5),将直线向上平移m(m>0)个单位,若平移后得到的直线与半径为6的⊙O相交(点O为坐标原点),则m的取值范围为 .三、解答题
-
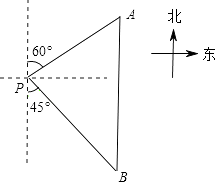
19. 求值:(﹣1)2018+|1﹣ |﹣20. 解方程: ﹣ =1.21. 已知:x2﹣y2=12,x+y=3,求2x2﹣2xy的值.22. 如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向的B处,求此时轮船所在的B处与灯塔P的距离.(参考数据: ≈2.449,结果保留整数)
 23. 九年级一班开展了“读一本好书”的活动,班委会对学生阅读书籍的情况进行了问卷调查,问卷设置了“小说”“戏剧”“散文”“其他”四个选项,每位同学仅选一项,根据调查结果绘制了如下不定整的频数分布表和扇形统计图.
23. 九年级一班开展了“读一本好书”的活动,班委会对学生阅读书籍的情况进行了问卷调查,问卷设置了“小说”“戏剧”“散文”“其他”四个选项,每位同学仅选一项,根据调查结果绘制了如下不定整的频数分布表和扇形统计图.类别
频数(人数)
频率
小说
16
戏剧
4
散文
a
其他
b
合计
1

根据图表提供的信息,解答下列问题:
(1)、直接写出a,b,m的值;(2)、在调查问卷中,甲、乙、丙、丁四位同学选择了“戏剧”类,现从以上四位同学中任意选出2名同学参加学校的戏剧兴趣小组,请用列表法或画树状图的方法,求选取的2人恰好乙和丙的概率.24. 如图,在Rt△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,连接CD,过E作EF∥DC交BC的延长线于F. (1)、证明:四边形CDEF是平行四边形;(2)、若四边形CDEF的周长是25cm,AC的长为5cm,求线段AB的长度.25. 某学校计划购买排球、篮球,已知购买1个排球与1个篮球的总费用为180元;3个排球与2个篮球的总费用为420元.(1)、求购买1个排球、1个篮球的费用分别是多少元?(2)、若该学校计划购买此类排球和篮球共60个,并且篮球的数量不超过排球数量的2倍.求至少需要购买多少个排球?并求出购买排球、篮球总费用的最大值?26. 如图,A(4,3)是反比例函数y= 在第一象限图象上一点,连接OA,过A作AB∥x轴,截取AB=OA(B在A右侧),连接OB,交反比例函数y= 的图象于点P.
(1)、证明:四边形CDEF是平行四边形;(2)、若四边形CDEF的周长是25cm,AC的长为5cm,求线段AB的长度.25. 某学校计划购买排球、篮球,已知购买1个排球与1个篮球的总费用为180元;3个排球与2个篮球的总费用为420元.(1)、求购买1个排球、1个篮球的费用分别是多少元?(2)、若该学校计划购买此类排球和篮球共60个,并且篮球的数量不超过排球数量的2倍.求至少需要购买多少个排球?并求出购买排球、篮球总费用的最大值?26. 如图,A(4,3)是反比例函数y= 在第一象限图象上一点,连接OA,过A作AB∥x轴,截取AB=OA(B在A右侧),连接OB,交反比例函数y= 的图象于点P.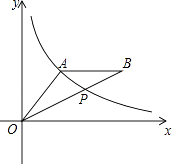 (1)、求反比例函数y= 的表达式;(2)、求点B的坐标;(3)、求△OAP的面积.27. 如图,AB是⊙O的直径,点E为线段OB上一点(不与O,B重合),作EC⊥OB,交⊙O于点C,作直径CD,过点C的切线交DB的延长线于点P,作AF⊥PC于点F,连接CB.
(1)、求反比例函数y= 的表达式;(2)、求点B的坐标;(3)、求△OAP的面积.27. 如图,AB是⊙O的直径,点E为线段OB上一点(不与O,B重合),作EC⊥OB,交⊙O于点C,作直径CD,过点C的切线交DB的延长线于点P,作AF⊥PC于点F,连接CB.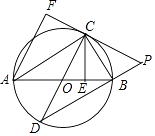 (1)、求证:AC平分∠FAB;(2)、求证:BC2=CE•CP;(3)、当AB=4 且 = 时,求劣弧 的长度.28. 如图,抛物线y=x2+bx+c与x轴交于A、B两点,B点坐标为(4,0),与y轴交于点C(0,4).
(1)、求证:AC平分∠FAB;(2)、求证:BC2=CE•CP;(3)、当AB=4 且 = 时,求劣弧 的长度.28. 如图,抛物线y=x2+bx+c与x轴交于A、B两点,B点坐标为(4,0),与y轴交于点C(0,4).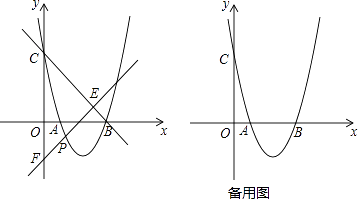 (1)、求抛物线的解析式;(2)、点P在x轴下方的抛物线上,过点P的直线y=x+m与直线BC交于点E,与y轴交于点F,求PE+EF的最大值;
(1)、求抛物线的解析式;(2)、点P在x轴下方的抛物线上,过点P的直线y=x+m与直线BC交于点E,与y轴交于点F,求PE+EF的最大值;
(3)、点D为抛物线对称轴上一点.①当△BCD是以BC为直角边的直角三角形时,直接写出点D的坐标;
②若△BCD是锐角三角形,直接写出点D的纵坐标n的取值范围.