河南省新乡市2017-2018学年高一下学期数学期末考试试卷
试卷更新日期:2018-07-25 类型:期末考试
一、单选题
-
1. 下列给出的赋值语句中正确的是( )A、 B、 C、 D、2. 下列函数中,既是偶函数,又是周期函数的是( )A、 B、 C、 D、3. 在 中,若 ,则 是( )A、锐角三角形 B、钝角三角形 C、直角三角形 D、形状不确定4. 某程序框图如图所示,则输出的 ( )
 A、3 B、6 C、10 D、155. ( )A、1 B、-1 C、 D、6. 已知函数 ,若 ,则 ( )A、-2020 B、2019 C、-2018 D、20177. 已知向量 , ,且 ,则 ( )A、 B、 C、 D、8. 执行如图所示的程序框图,若输入的 与输出的 相等,则 ( )
A、3 B、6 C、10 D、155. ( )A、1 B、-1 C、 D、6. 已知函数 ,若 ,则 ( )A、-2020 B、2019 C、-2018 D、20177. 已知向量 , ,且 ,则 ( )A、 B、 C、 D、8. 执行如图所示的程序框图,若输入的 与输出的 相等,则 ( ) A、1 B、0或1或2 C、1或2 D、0或29. 已知函数 的部分图象如图所示,为了得到 的图象,可以将 的图象( )
A、1 B、0或1或2 C、1或2 D、0或29. 已知函数 的部分图象如图所示,为了得到 的图象,可以将 的图象( )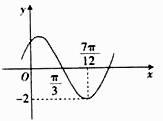 A、向右平移 个单位长度 B、向左平移 个单位长度 C、向右平移 个单位长度 D、向左平移 个单位长度10. 设 , , ,则 , , 的大小关系为( )A、 B、 C、 D、11. 向边长为1的正方形 内随机投入 粒芝麻,假定这些芝麻全部均匀地落入该正方形中,发现有 粒芝麻离点 的距离不大于1,则用随机模拟的方法得到的圆周率 的近似值为( )A、 B、 C、 D、12. 已知函数 ,对任意的 ,方程 有两个不同的实数根,则 的取值范围为( )A、 B、 C、 D、
A、向右平移 个单位长度 B、向左平移 个单位长度 C、向右平移 个单位长度 D、向左平移 个单位长度10. 设 , , ,则 , , 的大小关系为( )A、 B、 C、 D、11. 向边长为1的正方形 内随机投入 粒芝麻,假定这些芝麻全部均匀地落入该正方形中,发现有 粒芝麻离点 的距离不大于1,则用随机模拟的方法得到的圆周率 的近似值为( )A、 B、 C、 D、12. 已知函数 ,对任意的 ,方程 有两个不同的实数根,则 的取值范围为( )A、 B、 C、 D、二、填空题
-
13. 函数 的最小正周期是 .14. 从编号为01,02,…,50的50个产品中用系统抽样的方法抽取一个样本,已知样本中的前两个编号分别为03,08(编号按从小到大的顺序排列),则样本中最大的编号是 .15. 在平行四边形 中, , , ,点 , 分别在边 , 上(不与端点重合),且 ,则 的取值范围为 .16. 有下列命题
①已知 , 都是第一象限角,若 ,则 ;②已知 , 是钝角 中的两个锐角,则 ;③若 , , 是相互不互线的平面向量,则 与 垂直;④若 , 是平面向量的一组基底,则 , 可作为平面向量的另一组基底.其中正确的命题是(填写所有正确命题的编号).
三、解答题
-
17. 从高一年级某科月考成绩中随机抽取 名学生的成绩,绘制如图所示的频率分布直方图,若分数在 内的人数为30.
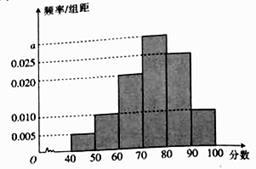 (1)、求 ;(2)、估计这次月考成绩的平均分(同一组中的数据用该组区间的中点值作代表).18. 设向量 , , .(1)、若 ,求 ;(2)、若 ,且 ,求 .19. 如图,在 中, , 是 的中点,设 , .
(1)、求 ;(2)、估计这次月考成绩的平均分(同一组中的数据用该组区间的中点值作代表).18. 设向量 , , .(1)、若 ,求 ;(2)、若 ,且 ,求 .19. 如图,在 中, , 是 的中点,设 , .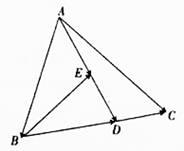 (1)、试用 , 表示 ;(2)、若 , ,且 与 的夹角为 ,求 .20. 盒子里放有外形相同且编号为1,2,3,4,5的五个小球,其中1号与2号是黑球,3号、4号与5号是红球,从中有放回地每次取出1个球,共取两次.(1)、求取到的2个球中恰好有1个是黑球的概率;(2)、求取到的2个球中至少有1个是红球的概率.21. 近年来,某市实验中学校领导审时度势,深化教育教学改革,经过师生共同努力,高考成绩硕果累累,捷报频传,尤其是2017年某著名高校在全国范围内录取的大学生中就有25名来自该中学.下表为该中学近5年被录取到该著名高校的学生人数.(记2013年的年份序号为1,2014年的年份序号为2,依此类推……)
(1)、试用 , 表示 ;(2)、若 , ,且 与 的夹角为 ,求 .20. 盒子里放有外形相同且编号为1,2,3,4,5的五个小球,其中1号与2号是黑球,3号、4号与5号是红球,从中有放回地每次取出1个球,共取两次.(1)、求取到的2个球中恰好有1个是黑球的概率;(2)、求取到的2个球中至少有1个是红球的概率.21. 近年来,某市实验中学校领导审时度势,深化教育教学改革,经过师生共同努力,高考成绩硕果累累,捷报频传,尤其是2017年某著名高校在全国范围内录取的大学生中就有25名来自该中学.下表为该中学近5年被录取到该著名高校的学生人数.(记2013年的年份序号为1,2014年的年份序号为2,依此类推……)年份序号
1
2
3
4
5
录取人数
10
13
17
20
25
参考数据: , .
参考公式: , .
(1)、求 关于 的线性回归方程,并估计2018年该中学被该著名高校录取的学生人数(精确到整数);
(2)、若在第1年和第4年录取的大学生中按分层抽样法抽取6人,再从这6人中任选2人,求这2人中恰好有一位来自第1年的概率.22. 已知 的三个内角分别为 , , ,且 .(1)、求 ;(2)、已知函数 ,若函数 的定义域为 ,求函数 的值域.