河南省濮阳市2017-2018学年高一下学期理数升级考试试卷
试卷更新日期:2018-07-25 类型:期末考试
一、单选题
-
1. 已知角 的终边经过点 ,则 ( )A、 B、 C、 D、2. 在利用最小二乘法求回归方程 时,用到了下面表中的 组数据,则表格中 的值为( )A、 B、 C、 D、3. 已知集合 , ,则下列结论正确的是( )A、 B、 C、 D、4. 若直线 与圆 相切,则 的值是( )A、 或 B、 或 C、 或 D、 或5. 一程序框图如图所示,如果输出的函数值在区间 上,那么输入的实数 的取值范围是( )
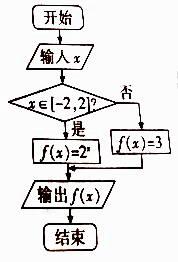 A、 B、 C、 D、6. 一个几何体的三视图如图所示,已知这个几何体放入体积为 ,则 为( )
A、 B、 C、 D、6. 一个几何体的三视图如图所示,已知这个几何体放入体积为 ,则 为( )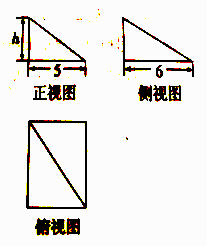 A、 B、 C、 D、7. 若向量 , 不共线, , , ,则下列关系式中正确的是( )A、 B、 C、 D、8. 若 ,则 ( )A、 B、 C、 D、9. 已知 ,则函数 有零点的概率为( )A、 B、 C、 D、10. 已知 是定义在 上的偶函数,且在区间 上单调递增.若实数 满足 ,则 的取值范围是( )A、 B、 C、 D、11. 若将函数 的图形向右平移 个单位,所得图象关于 轴对称,则 的最小正值是( )A、 B、 C、 D、12. 已知圆 及三个函数:① ;② ;③ 其中图像能等分圆 面积的函数个数为( )
A、 B、 C、 D、7. 若向量 , 不共线, , , ,则下列关系式中正确的是( )A、 B、 C、 D、8. 若 ,则 ( )A、 B、 C、 D、9. 已知 ,则函数 有零点的概率为( )A、 B、 C、 D、10. 已知 是定义在 上的偶函数,且在区间 上单调递增.若实数 满足 ,则 的取值范围是( )A、 B、 C、 D、11. 若将函数 的图形向右平移 个单位,所得图象关于 轴对称,则 的最小正值是( )A、 B、 C、 D、12. 已知圆 及三个函数:① ;② ;③ 其中图像能等分圆 面积的函数个数为( )
A、 B、 C、 D、二、填空题
-
13. 若函数 如下表所示:
则 .
14. 已知一个正方体的所有顶点在一个球面上,若这个正方体的表面积为 ,则这个球的体积为 .15. 设点 是圆 上的动点,点 是直线 上的动点,则 的最小值为 .16. 在 中, , , 是斜边 上的两个动点,且 ,则 的取值范围为 .三、解答题
-
17. 某商场举行有奖促销活动,顾客购买一定金额的商品后即可抽奖.抽奖方法是:从装有 个红球 , 和 个白球 的甲箱与装有 个红球 , 和 个白球 , 的乙箱中,各随机摸出 个球,若模出的 个球都是红球则中奖,否则不中奖.(1)、用球的标号列出所有可能的模出结果;(2)、有人认为:两个箱子中的红球比白球多所以中奖的概率大于不中奖的概率,你认为正确吗?请说明理由.18. 在每年的3月份,濮阳市政府都会发动市民参与到植树绿化活动中去林业管理部门为了保证树苗的质量都会在植树前对树苗进行检测,现从甲、乙两种树苗中各抽测了 株树苗,量出它们的高度如下(单位:厘米),
甲:37,21,31,20,29,19,32,23,25,33;
乙:10,30,47,27,46,14,26,10,44,46.
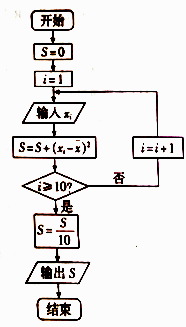 (1)、画出两组数据的茎叶图并根据茎叶图对甲、乙两种树苗的高度作比较,写出两个统计结论;(2)、设抽测的 株甲种树苗高度平均值为 ,将这 株树苗的高度依次输人,按程序框(如图)进行运算,问输出的 大小为多少?并说明 的统计学意义,19. 如图,在底面是正方形的四棱锥 中, 面 , 交 于点 , 是 中点, 为 上一点.
(1)、画出两组数据的茎叶图并根据茎叶图对甲、乙两种树苗的高度作比较,写出两个统计结论;(2)、设抽测的 株甲种树苗高度平均值为 ,将这 株树苗的高度依次输人,按程序框(如图)进行运算,问输出的 大小为多少?并说明 的统计学意义,19. 如图,在底面是正方形的四棱锥 中, 面 , 交 于点 , 是 中点, 为 上一点. (1)、求证: BD⊥FG .(2)、确定点 在线段 上的位置,使 平面 ,并说明理由.20. 已知函数 的最大值为 .
(1)、求证: BD⊥FG .(2)、确定点 在线段 上的位置,使 平面 ,并说明理由.20. 已知函数 的最大值为 . (1)、求 的值及 的最小正周期;(2)、在坐标系上作出 在 上的图像,要求标出关键点的坐标.21. 四边形 中, , , , .(1)、求 与 的关系式;(2)、若 ,求 、 的值以及四边形 的面积.22. 辽宁号航母纪念章从2012年10月5日起开始上市,通过市场调查,得到该纪念章每 枚的市场价 (单位:元)与上市时间 (单位:天)的数据如下:
(1)、求 的值及 的最小正周期;(2)、在坐标系上作出 在 上的图像,要求标出关键点的坐标.21. 四边形 中, , , , .(1)、求 与 的关系式;(2)、若 ,求 、 的值以及四边形 的面积.22. 辽宁号航母纪念章从2012年10月5日起开始上市,通过市场调查,得到该纪念章每 枚的市场价 (单位:元)与上市时间 (单位:天)的数据如下:上市时间 天
市场价 元
(1)、根据上表数据,从下列函数中选取一个恰当的函数描述辽宁号航母纪念章的市场价 与上市时间 的变化关系:① ;② ;③ ;(2)、利用你选取的函数,求辽宁号航母纪念章市场价最低时的上市天数及最低的价格;(3)、设你选取的函数为 ,若对任意实数 ,关于 的方程 恒有两个想异实数根,求 的取值范围.