福建省南平市2017-2018学年高一下学期数学期末质量检测卷
试卷更新日期:2018-07-25 类型:期末考试
一、单选题
-
1. 集合 ,则集合 中含有的元素个数是( )A、2 B、3 C、5 D、62. 如果 ,那么下列不等式一定成立的是( )A、 B、 C、 D、3. 若 ,则 等于( )A、 B、 C、 D、4. 不等式 的解集为 ,则函数 的图象大致为( )A、
 B、
B、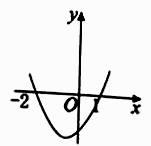 C、
C、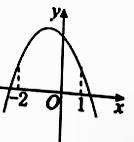 D、
D、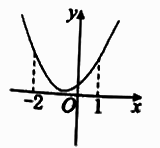 5. 《九章算术》是我国古代的数学名著,书中《均属章》有如下问题:今有五人分六钱,令前三人所得与后二人等,各人所得均增,问各得几何?其意思是“已知 ”五个人分重量为6钱(“钱”是古代的一种重量单位)的物品, 三人所得钱数之和与 二人所得钱数之和相同,且 每人所得钱数依次成递增等差数列,问五个人各分得多少钱的物品?”在这个问题中, 分得物品的钱数是( )A、 钱 B、 钱 C、 钱 D、 钱6. 若原点 和点 在直线 的两侧,则实数 的取值范围是( )A、 B、 C、 D、7. 已知向量 , ,且 ,则 的值为( )A、2 B、3 C、4 D、58. 若将函数 的图象向左平移 个单位长度,则平移后图象的一条对称轴为( )A、 B、 C、 D、9. 如图是函数 的部分图象,已知函数图象经过 两点,则 ( )
5. 《九章算术》是我国古代的数学名著,书中《均属章》有如下问题:今有五人分六钱,令前三人所得与后二人等,各人所得均增,问各得几何?其意思是“已知 ”五个人分重量为6钱(“钱”是古代的一种重量单位)的物品, 三人所得钱数之和与 二人所得钱数之和相同,且 每人所得钱数依次成递增等差数列,问五个人各分得多少钱的物品?”在这个问题中, 分得物品的钱数是( )A、 钱 B、 钱 C、 钱 D、 钱6. 若原点 和点 在直线 的两侧,则实数 的取值范围是( )A、 B、 C、 D、7. 已知向量 , ,且 ,则 的值为( )A、2 B、3 C、4 D、58. 若将函数 的图象向左平移 个单位长度,则平移后图象的一条对称轴为( )A、 B、 C、 D、9. 如图是函数 的部分图象,已知函数图象经过 两点,则 ( ) A、 B、 C、 D、10. 已知数列 中,若 ,则该数列的通项公式 ( )A、 B、 C、 D、11. 在 中, ,则 的最大值为( )A、2 B、3 C、4 D、512. 已知函数 ,且 ,则 ( )
A、 B、 C、 D、10. 已知数列 中,若 ,则该数列的通项公式 ( )A、 B、 C、 D、11. 在 中, ,则 的最大值为( )A、2 B、3 C、4 D、512. 已知函数 ,且 ,则 ( )
A、20100 B、20500 C、40100 D、10050二、填空题
-
13. 函数 的最小正周期为.14. 设实数 满足约束条件 ,则 的取值范围是.15. 矩形 的两条对角线交于点 ,已知点 为线段 的中点,若 ,其中 为实数,则 的值为.16. 函数 ,若 时有 恒成立,则 的取值范围是.
三、解答题
-
17. 设函数 .(1)、求函数 的单调递减区间;(2)、若 ,求函数 的值域.18. 已知函数 .(1)、当 时,解关于 的不等式 ;(2)、若 ,解关于 的不等式 .19. 已知 为的三个内角 的对边,向量 , ,且 .(1)、求角 的大小;(2)、若 ,求 的值及 的面积.