2017高考数学备考复习（理科）专题十七：随机变量及其分布列

试卷更新日期：2017-02-10 类型：一轮复习

进入出卷网下载

一、单选题

1. 某计算机网络有n个终端，每个终端在一天中使用的概率为p，则这个网络中一天中平均使用的终端个数为（　　）

A、np(1-p) B、np C、n(1-p) D、p(1-p)

查看试题解析
2. 抛掷红、蓝两个骰子，事件A=“红骰子出现4点”，事件B=“蓝骰子出现的点数是偶数”，则 $P (A | B)$ 为（）

A、 $\frac{1}{2}$ B、 $\frac{5}{36}$ C、 $\frac{1}{12}$ D、 $\frac{1}{6}$

查看试题解析
3.
某一部件由三个电子元件按下图方式连接而成，元件1或元件2正常工作，且元件3正常工作，则部件正常工作，设三个电子元件的使用寿命（单位：小时）均服从正态分布N(1000，50²)，且各个元件能否正常工作相互独立，那么该部件的使用寿命超过1000小时的概率为（）

A、 $\frac{1}{2}$ B、 $\frac{3}{8}$ C、 $\frac{1}{4}$ D、 $\frac{1}{8}$

查看试题解析
4. 某学生解选择题出错的概率为0.1，该生解三道选择题至少有一道出错的概率是（）

A、 $0 . 1^{2} \times 0.9$ B、 $0 . 1^{3} + 0 . 1^{2} \times 0.9 + 0.1 \times 0 . 9^{2}$ C、 $1 - 0 . 9^{3}$ D、 $0 . 1^{3}$

查看试题解析
5. 根据历年气象统计资料，宜都三月份吹东风的概率为 $\frac{9}{30}$ ，下雨的概率为 $\frac{11}{30}$ ，既吹东风又下雨的概率为 $\frac{8}{30}$ ．则在吹东风的条件下下雨的概率为（　　）

A、 $\frac{9}{11}$ B、 $\frac{8}{9}$ C、 $\frac{2}{5}$ D、 $\frac{8}{11}$

查看试题解析
6. 一个人有n把钥匙，其中只有一把可以打开房门，他随意的进行试开，若试开过的钥匙放在一边，试开次数X为随机变量，则P（X=k）=（）

A、 $\frac{k}{n}$ B、 $\frac{1}{n}$ C、 $\frac{k - 1}{n}$ D、 $\frac{k!}{n!}$

查看试题解析
7. 随机变量 $X$ 的概率分布规律为 $P (X = n) = \frac{a}{n (n + 1)}$ ， $(n = 1 ， 2 ， 3 ， 4)$ 其中 $a$ 是常数，则 $P (\frac{1}{2} < X < \frac{5}{2})$ 的值为（）

A、 $\frac{2}{3}$ B、 $\frac{3}{4}$ C、 $\frac{4}{5}$ D、 $\frac{5}{6}$

查看试题解析
8. 从一批羽毛球产品中任取一个，质量小于4.8g的概率是0.3，质量不小于4.85g的概率是0.32，那么质量在[4.8，4.85）g范围内的概率是（）

A、0.62 B、0.38 C、0.7 D、0.68

查看试题解析
9. 来晋江旅游的外地游客中，若甲、乙、丙三人选择去五店市游览的概率均为 $\frac{3}{5}$ ，且他们的选择互不影响，则这三人中至多有两人选择去五店市游览的概率为（　　）

A、 $\frac{36}{125}$ B、 $\frac{44}{125}$ C、 $\frac{54}{125}$ D、 $\frac{98}{125}$

查看试题解析
10. 已知离散型随机变量X的分布列为
X
1
2
3
P
$\frac{3}{5}$
$\frac{3}{10}$
$\frac{1}{10}$
则X的数学期望E（X）=（）

A、 $\frac{3}{2}$ B、2 C、 $\frac{5}{2}$ D、3

查看试题解析
11. 若随机变量X服从正态分布，其正态曲线上的最高点的坐标是（10， $\frac{1}{2}$ ），则该随机变量的方差等于（）

A、10 B、100 C、 $\frac{2}{π}$ D、 $\sqrt{\frac{2}{π}}$

查看试题解析
12. 已知随机变量ξ服从正态分布 $N (2 ， σ^{2})$ ， P（ξ≤4）=0.84，则P（ξ≤0）等于（）

A、0.16 B、0.32 C、0.68 D、0.84

查看试题解析
13. 一次抛掷两枚质地均匀的骰子，当至少有一枚5点或一枚6点时，即认定这次试验成功．则在10次试验中成功次数X的数学期望为 ( )

A、 $\frac{10}{3}$ B、 $\frac{20}{3}$ C、 $\frac{50}{9}$ D、 $\frac{200}{81}$

查看试题解析
14. 已知随机变量X～B(6，0.4)，则当η＝－2X＋1时，D(η)＝(　　)

A、－1.88 B、－2.88 C、5. 76 D、6.76

查看试题解析
15. 某种种子每粒发芽的概率都为0.9，现播种了1 000粒，对于没有发芽的种子，每粒需再补种2粒，补种的种子数记为X ，则X的均值为(　　)

A、100 B、200 C、300 D、400

查看试题解析

二、填空题

16. 在某项测量中，测量结果ξ服从正态分布N（1，σ²）（σ＞0），若ξ在（0，2）内取值的概率为0.8，则ξ在（﹣∞，2]内取值的概率为．

查看试题解析
17. 同时抛掷两枚质地均匀的硬币，当至少有一枚硬币正面向上时，就说这次试验成功，则在2次试验中成功次数X的均值是　　．

查看试题解析
18. 一名射手击中靶心的概率是0.9，如果他在同样的条件下连续射击10次，则他击中靶心的次数的均值是．

查看试题解析
19. 已知随机变量ξ的分布列为
ξ
﹣2
﹣1
0
1
2
3
P
$\frac{1}{12}$
$\frac{3}{12}$
$\frac{4}{12}$
$\frac{1}{12}$
$\frac{2}{12}$
$\frac{1}{12}$
若P（ξ²＞x）= $\frac{1}{12}$ ，则实数x的取值范围是．

查看试题解析
20. 一个兴趣学习小组由12男生6女生组成，从中随机选取3人作为领队，记选取的3名领队中男生的人数为X，则X的期望E（X）= ．

查看试题解析

三、解答题

21.
某厂用鲜牛奶在某台设备上生产 $A ， B$ 两种奶制品．生产1吨A产品需鲜牛奶2吨，使用设备1小时，获利1000元；生产1吨B产品需鲜牛奶1.5吨，使用设备1.5小时，获利1200元．要求每天B产品的产量不超过A产品产量的2倍，设备每天生产 $A ， B$ 两种产品时间之和不超过12小时. 假定每天可获取的鲜牛奶数量W（单位：吨）是一个随机变量，其分布列为
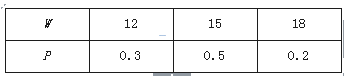
（Ⅰ）求Z的分布列和均值；该厂每天根据获取的鲜牛奶数量安排生产，使其获利最大，因此每天的最大获利Z（单位：元）是一个随机变量．
（Ⅱ）若每天可获取的鲜牛奶数量相互独立，求3天中至少有1天的最大获利超过10000元的概率．

查看试题解析
22. 为评估设备M生产某种零件的性能，从设备M生产零件的流水线上随机抽取100件零件最为样本，测量其直径后，整理得到下表：
直径/mm
58
59
61
62
63
64
65
66
67
68
69
70
71
73
合计
件数
1
1
3
5
6
19
33
18
4
4
2
1
2
1
100
经计算，样本的平均值μ=65，标准差=2.2，以频率值作为概率的估计值．
（1）为评判一台设备的性能，从该设备加工的零件中任意抽取一件，记其直径为X，并根据以下不等式进行评判（p表示相应事件的频率）：①p（μ﹣σ＜X≤μ+σ）≥0.6826．②P（μ﹣σ＜X≤μ+2σ）≥0.9544③P（μ﹣3σ＜X≤μ+3σ）≥0.9974．评判规则为：若同时满足上述三个不等式，则设备等级为甲；仅满足其中两个，则等级为乙，若仅满足其中一个，则等级为丙；若全部不满足，则等级为丁．试判断设备M的性能等级．
（2）将直径小于等于μ﹣2σ或直径大于μ+2σ的零件认为是次品
（i）从设备M的生产流水线上随意抽取2件零件，计算其中次品个数Y的数学期望EY；
（ii）从样本中随意抽取2件零件，计算其中次品个数Z的数学期望EZ．

查看试题解析
23. 甲、乙两袋中各装有大小相同的小球9个，其中甲袋中红色、黑色、白色小球的个数分别为2个、3个、4个，乙袋中红色、黑色、白色小球的个数均为3个，某人用左右手分别从甲、乙两袋中取球．
（1）若左右手各取一球，问两只手中所取的球颜色不同的概率是多少？
（2）若左右手依次各取两球，称同一手中两球颜色相同的取法为成功取法，记两次取球的成功取法次数为X，求X的分布列和数学期望．

查看试题解析
24. 某单位招聘面试，每次从试题库随机调用一道试题，若调用的是A类型试题，则使用后该试题回库，并增补一道A类试题和一道B类型试题入库，此次调题工作结束；若调用的是B类型试题，则使用后该试题回库，此次调题工作结束．试题库中现共有n+m道试题，其中有n道A类型试题和m道B类型试题，以X表示两次调题工作完成后，试题库中A类试题的数量．
（Ⅰ）求X=n+2的概率；
（Ⅱ）设m=n，求X的分布列和均值（数学期望）

查看试题解析

四、综合题

25. 某小组共10人，利用假期参加义工活动，已知参加义工活动次数为1,2,3的人数分别为3,3,4,. 现从这10人中随机选出2人作为该组代表参加座谈会.

(1)、设A为事件“选出的2人参加义工活动次数之和为4”，求事件A发生的概率；

(2)、设 $X$ 为选出的2人参加义工活动次数之差的绝对值，求随机变量 $X$ 的分布列和数学期望.

查看试题解析

ξ	﹣2	﹣1	0	1	2	3
P	$\frac{1}{12}$	$\frac{3}{12}$	$\frac{4}{12}$	$\frac{1}{12}$	$\frac{2}{12}$	$\frac{1}{12}$

直径/mm	58	59	61	62	63	64	65	66	67	68	69	70	71	73	合计
件数	1	1	3	5	6	19	33	18	4	4	2	1	2	1	100

X	1	2	3
P	$\frac{3}{5}$	$\frac{3}{10}$	$\frac{1}{10}$