2017高考数学备考复习(理科)专题十四:圆锥曲线与方程
试卷更新日期:2017-02-10 类型:一轮复习
一、单选题
-
1. 与椭圆共焦点且过点P(2,1)的双曲线方程是( )
A、 B、 C、 D、2. 椭圆的左、右焦点分别为 , 弦AB过 , 若的内切圆周长为 , A,B两点的坐标分别为和 , 则的值为( )
A、 B、 C、 D、3. 已知双曲线 , 则它的渐近线的方程为( )A、 B、 C、 D、4.如图,椭圆的左、右顶点分别是A,B,左、右焦点分别是F1 , F2 , 若|AF1|,|F1F2|,|F1B|成等比数列,则此椭圆的离心率为()
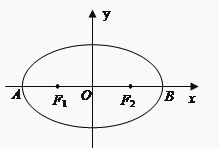 A、 B、 C、 D、5. 若椭圆(a>b>0)的离心率为 , 则双曲线的渐近线方程为( )
A、 B、 C、 D、5. 若椭圆(a>b>0)的离心率为 , 则双曲线的渐近线方程为( )
A、y=±x B、y=±x C、y=±x D、y=±x6. 抛物线的准线与双曲线的两条渐近线所围成的三角形面积等于( )
A、 B、 C、2 D、7. 过双曲线 x2-=1的右焦点且与x轴垂直的直线,交该双曲线的两条渐近线于A,B两点,则|AB|=( )A、 B、2 C、6 D、48. 已知A,B,P是双曲线上不同的三点,且A,B连线经过坐标原点,若直线PA,PB的斜率乘积kPA•kPB= , 则该双曲线的离心率为( )
A、 B、 C、 D、9. 正方体中,M为侧面所在平面上的一个动点,且M到平面的距离是M到直线BC距离的2倍,则动点M的轨迹为( )
A、椭圆 B、双曲线 C、抛物线 D、圆10.如图,、是双曲线的左、右焦点,过的直线与双曲线的左、右两个分支分别交于点、 , 若为等边三角形,则该双曲线的离心率为 ( )
 A、 B、 C、 D、11. 椭圆的弦被点平分,则此弦所在的直线方程是( )
A、 B、 C、 D、11. 椭圆的弦被点平分,则此弦所在的直线方程是( )
A、 B、 C、 D、12. 若双曲线 的左、右焦点分别为 , 点P在双曲线E上,且=3,则 等于( )A、11 B、9 C、5 D、313. 已知抛物线y2=2px(p>0)的准线经过点(-1,1),则抛物线焦点坐标为( )A、(-1,0) B、(1,0) C、(0,-1) D、(0,1)14. 若双曲线的一条渐近线经过点(3,-4),则此双曲线的离心率为( )A、 B、 C、 D、15. 已知抛物线的准线过双曲线的左焦点且与双曲线交于A、B两点,O为坐标原点,且△AOB的面积为 , 则双曲线的离心率为( )A、 B、4 C、3 D、216. 已知椭圆E的中心为坐标原点,离心率为 , E的右焦点与抛物线C:y2=8x的焦点重合,A,B是C的准线与E的两个交点,则|AB|= ( )A、3 B、6 C、9 D、1217. 已知O为坐标原点,F是椭圆C: =1(a>b>0)的左焦点,A,B分别为C的左,右顶点.P为C上一点,且PF⊥x轴,过点A的直线l与线段PF交于点M,与y轴交于点E.若直线BM经过OE的中点,则C的离心率为( )A、 B、 C、 D、18. 直线l经过椭圆的一个顶点和一个焦点,若椭圆中心到l的距离为其短轴长的 ,则该椭圆的离心率为( )A、 B、 C、 D、19. 已知双曲线与椭圆 的焦点重合,它们的离心率之和为 ,则双曲线的渐近线方程为( )A、 B、 C、 D、y=20. 已知椭圆C: + =1(a>b>0)的离心率为 ,与双曲线x2﹣y2=1的渐近线有四个交点,以这四个交点为顶点的四边形的面积为16,则椭圆C的方程为( )A、+ =1 B、+ =1 C、+ =1 D、+ =1二、填空题
-
21. 若椭圆长轴长与短轴长之比为2,它的一个焦点是 , 则椭圆的标准方程是22.
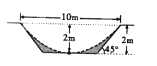
如图,一横截面为等腰梯形的水渠,因泥沙沉积,导致水渠截面边界呈抛物线型(图中虚线表示),则原始的最大流量与当前最大流量的比值为 .
 23. 平面直角坐标系xOy中,双曲线C1:的渐近线与抛物线交于点 , 若的垂心为的焦点,则的离心率为 .24.
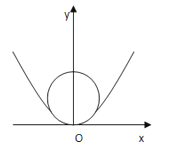
23. 平面直角坐标系xOy中,双曲线C1:的渐近线与抛物线交于点 , 若的垂心为的焦点,则的离心率为 .24.一个酒杯的轴截面是一条抛物线的一部分,它的方程是x2=2y,y∈[0,10],在杯内放入一个清洁球,要求清洁球能擦净酒杯的最底部(如图),则清洁球的最大半径为
 25. 设F为抛物线C:y2=4x的焦点,过点P(﹣1,0)的直线l交抛物线C于两点A,B,点Q为线段AB的中点,若|FQ|=2,则直线l的斜率等于 .
25. 设F为抛物线C:y2=4x的焦点,过点P(﹣1,0)的直线l交抛物线C于两点A,B,点Q为线段AB的中点,若|FQ|=2,则直线l的斜率等于 .三、综合题
-
26. 已知抛物线C:y2=2x的焦点为F,平行于x轴的两条直线l1 , l2分别交C于A,B两点,交C的准线于P,Q两点.(1)、若F在线段AB上,R是PQ的中点,证明AR∥FQ;(2)、若△PQF的面积是△ABF的面积的两倍,求AB中点的轨迹方程.27. 设抛物线C:x2=2py(p>0)的焦点为F,准线为l,A∈C,已知以F为圆心,FA为半径的圆F交l于B,D两点;(1)、若∠BFD=90°,△ABD的面积为 ,求p的值及圆F的方程;(2)、若A,B,F三点在同一直线m上,直线n与m平行,且n与C只有一个公共点,求坐标原点到m,n距离的比值.28. 已知椭圆C: =1(a>b>0)与y轴的交点为A,B(点A位于点B的上方),F为左焦点,原点O到直线FA的距离为 b.(1)、求椭圆C的离心率;(2)、设b=2,直线y=kx+4与椭圆C交于不同的两点M,N,求证:直线BM与直线AN的交点G在定直线上.29. 设椭圆 的左右顶点分别为A,B,点P在椭圆上且异于A,B两点,O为坐标原点.(1)、若直线AP与BP的斜率之积为 ,求椭圆的离心率;(2)、若|AP|=|OA|,证明直线OP的斜率k满足|k|> .30. 已知三点O(0,0),A(﹣2,1),B(2,1),曲线C上任意一点M(x,y)满足| + |= •( + )+2.(1)、求曲线C的方程;(2)、动点Q(x0 , y0)(﹣2<x0<2)在曲线C上,曲线C在点Q处的切线为直线l:是否存在定点P(0,t)(t<0),使得l与PA,PB都相交,交点分别为D,E,且△QAB与△PDE的面积之比是常数?若存在,求t的值.若不存在,说明理由.31. 在平面直角坐标系xOy中,F是抛物线C:x2=2py(p>0)的焦点,M是抛物线C上位于第一象限内的任意一点,过M,F,O三点的圆的圆心为Q,点Q到抛物线C的准线的距离为 .(1)、求抛物线C的方程;(2)、是否存在点M,使得直线MQ与抛物线C相切于点M?若存在,求出点M的坐标;若不存在,说明理由;(3)、若点M的横坐标为 ,直线l:y=kx+ 与抛物线C有两个不同的交点A,B,l与圆Q有两个不同的交点D,E,求当 ≤k≤2时,|AB|2+|DE|2的最小值.32. 如图,抛物线C1:x2=4y,C2:x2=﹣2py(p>0),点M(x0 , y0)在抛物线C2上,过M作C1的切线,切点为A,B(M为原点O时,A,B重合于O),当x0=1﹣ 时,切线MA的斜率为﹣ .
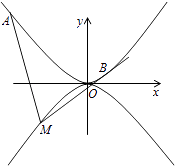 (1)、求P的值;(2)、当M在C2上运动时,求线段AB中点N的轨迹方程(A,B重合于O时,中点为O).
(1)、求P的值;(2)、当M在C2上运动时,求线段AB中点N的轨迹方程(A,B重合于O时,中点为O).