2017高考数学备考复习(理科)专题十二:空间向量与立体几何
试卷更新日期:2017-02-10 类型:一轮复习
一、单选题
-
1. 设平面α的法向量为(1,2,﹣2),平面β的法向量为(﹣2,﹣4,k),若α∥β,则k=( )A、2 B、-4 C、4 D、-22. 已知三棱柱ABC-A1B1C1的侧棱与底面边长都相等,A1在底面ABC内的射影为的中心,则AB1与底面ABC所成角的正弦值等于( )A、 B、 C、 D、3. 在直三棱柱中,底面是等腰直角三角形, , 侧棱 , D,E分别是与的中点,点E在平面ABD上的射影是的重心G.则与平面ABD所成角的余弦值 ()
A、 B、 C、 D、4. 如图,在空间直角坐标系中有直三棱柱, , 则直线与直线夹角的余弦值为( )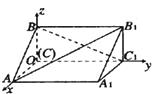 A、 B、 C、 D、5. 如图,四棱锥P-ABCD中,底面ABCD是矩形,PD⊥平面ABCD,且PD=AD=1,AB=2,点E是AB上一点,当二面角P-EC-D的平面角为时,AE=( )
A、 B、 C、 D、5. 如图,四棱锥P-ABCD中,底面ABCD是矩形,PD⊥平面ABCD,且PD=AD=1,AB=2,点E是AB上一点,当二面角P-EC-D的平面角为时,AE=( )
A、1 B、 C、2- D、2-6. 如图,已知长方体中, , , 则二面角的余弦值为( )
A、 B、 C、 D、7. 已知E,F分别是正方体ABCD﹣A1B1C1D1的棱BC,CC1的中点,则截面AEFD1与底面ABCD所成二面角的正弦值是( ) A、 B、 C、 D、8. 已知三条不重合的直线m,n,l和两个不重合的平面α、β,下列命题中正确命题个数为( )
A、 B、 C、 D、8. 已知三条不重合的直线m,n,l和两个不重合的平面α、β,下列命题中正确命题个数为( )
①若 , 则 ; ②若且则
③ 若 则 ④若 , 则
A、1 B、2 C、3 D、49. 如图,平面ABCD平面ABEF,四边形ABCD是正方形,四边形ABEF是矩形,且 , G是EF的中点,则GB与平面AGC所成角的正弦值为( )
A、 B、 C、 D、10. 如图,斜线段AB与平面 所成的角为60 , B为斜足,平面 上的动点P满足 PAB=30 , 则点P的轨迹是()
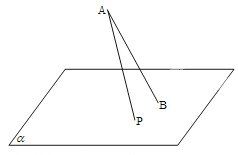 A、直线 B、抛物线 C、椭圆 D、双曲线的一支11. 如图,设正方体ABCD﹣A1B1C1D1的棱长为1,则直线B1C与平面AB1D1所成的角是( )
A、直线 B、抛物线 C、椭圆 D、双曲线的一支11. 如图,设正方体ABCD﹣A1B1C1D1的棱长为1,则直线B1C与平面AB1D1所成的角是( ) A、 B、arccos C、 D、arccos12. 若直线l的方向向量为 , 平面α的法向量为 , 能使l∥α的是( )A、=(1,0,0),=(﹣2,0,0) B、=(1,3,5),=(1,0,1) C、=(0,2,1),=(﹣1,0,﹣1) D、=(1,﹣1,3),=(0,3,1)13. 如图所示的长方体中,AB=2 ,AD= , = ,E、F分别为 的中点,则异面直线DE、BF所成角的大小为( )
A、 B、arccos C、 D、arccos12. 若直线l的方向向量为 , 平面α的法向量为 , 能使l∥α的是( )A、=(1,0,0),=(﹣2,0,0) B、=(1,3,5),=(1,0,1) C、=(0,2,1),=(﹣1,0,﹣1) D、=(1,﹣1,3),=(0,3,1)13. 如图所示的长方体中,AB=2 ,AD= , = ,E、F分别为 的中点,则异面直线DE、BF所成角的大小为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
14. 已知向量=(1,1,0),=(﹣1,0,2),且k+与2-互相垂直,则k值是15. 如图,正三棱柱ABC﹣A1B1C1的各棱长相等,点D是棱CC1的中点,则AA1与面ABD所成角的大小是
 16. 已知空间三点A(1,1,1)、B(﹣1,0,4)、C(2,﹣2,3),则与的夹角θ的大小是17. 已知A,B,C的坐标分别为(0,1,0),(﹣1,0,﹣1),(2,1,1),点P的坐标是(x,0,y),若PA⊥平面ABC,则点P的坐标是18. 将正方形ABCD沿对角线BD折成直二面角A﹣BC﹣C,有如下四个结论:
16. 已知空间三点A(1,1,1)、B(﹣1,0,4)、C(2,﹣2,3),则与的夹角θ的大小是17. 已知A,B,C的坐标分别为(0,1,0),(﹣1,0,﹣1),(2,1,1),点P的坐标是(x,0,y),若PA⊥平面ABC,则点P的坐标是18. 将正方形ABCD沿对角线BD折成直二面角A﹣BC﹣C,有如下四个结论:①AC⊥BD;②△ABC是等边三角形;
③AB与CD所成的角90°;④二面角A﹣BC﹣D的平面角正切值是;
其中正确结论是 (写出所有正确结论的序号)
三、解答题
-
19. 如图,四棱锥P﹣ABCD中,PA⊥平面ABCD,四边形ABCD是矩形,E,F分别是AB,PD的中点,若PA=AD=3,CD=
①求证:AF∥平面PCE
②求证:平面PCE⊥平面PCD
③求直线FC与平面PCE所成角的正弦值.
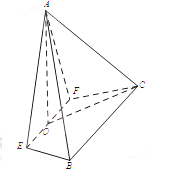
 20. 如图,在四棱锥A-EFCB中, 为等边三角形,平面AEF 平面EFCB, ,
20. 如图,在四棱锥A-EFCB中, 为等边三角形,平面AEF 平面EFCB, ,, , , O为EF的中点.
(Ⅰ)求证: ;
(Ⅱ)求二面角F-AE-B的余弦值;
(Ⅲ)若BE 平面AOC,求a的值.
 21. 如图,在几何体ABCDE中,四边形ABCD是矩形,AB⊥平面BEC,BE⊥EC,AB=BE=EC=2,G,F分别是线段BE,DC的中点.
21. 如图,在几何体ABCDE中,四边形ABCD是矩形,AB⊥平面BEC,BE⊥EC,AB=BE=EC=2,G,F分别是线段BE,DC的中点.(Ⅰ)求证:BE//平面ADE ;
(Ⅱ)求平面AEF与平面BEC所成锐二面角的余弦值.
 22. 如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°.
22. 如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°.(Ⅰ)求证:AC⊥平面BDE;
(Ⅱ)求二面角F﹣BE﹣D的余弦值.

四、综合题
-
23. 如图1,在Rt△ABC中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,且DE∥BC,DE=2,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图2.
 (1)、求证:A1C⊥平面BCDE;(2)、若M是A1D的中点,求CM与平面A1BE所成角的大小;(3)、线段BC上是否存在点P,使平面A1DP与平面A1BE垂直?说明理由.
(1)、求证:A1C⊥平面BCDE;(2)、若M是A1D的中点,求CM与平面A1BE所成角的大小;(3)、线段BC上是否存在点P,使平面A1DP与平面A1BE垂直?说明理由.

