2017高考数学备考复习（理科）专题十：不等式

试卷更新日期：2017-02-10 类型：一轮复习

进入出卷网下载

一、单选题

1. 设x，y满足约束条件 $\{\begin{matrix} \begin{matrix} x - y + 2 ⩾ 0 \\ 4 x - y - 4 ⩽ 0 \\ x ⩾ 0 \end{matrix} \\ y ⩾ 0 \end{matrix}$ ，若目标函数 $z = a x + b y (a > 0 ， b > 0)$ 的最大值为6，则 $\frac{1}{a} + \frac{2}{b}$ 的最小值为

A、1 B、3 C、2 D、4

查看试题解析
2. 已知 $a > 0 ， b > 0$ ，以下三个结论：① $\frac{2 a b}{a + b} \leq \frac{a + b}{2}$ ， ② $\frac{a + b}{2} \leq \sqrt{\frac{a^{2} + b^{2}}{2}}$ ③ $\frac{b^{2}}{a} \leq \frac{a^{2}}{b}$ ，其中正确的个数是（）

A、0 B、1 C、2 D、3

查看试题解析
3. 如图阴影部分用二元一次不等式组表示为( )

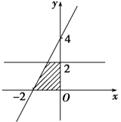
A、 $\{\begin{matrix} y \leq 2 \\ 2 x - y + 4 \geq 0 \end{matrix}$ B、 ${\begin{matrix} 0 \leq y \leq 2 \\ x \leq 0 \\ 2 x - y + 4 \geq 0 \end{matrix}$ C、 ${\begin{matrix} y \leq 2 \\ x \leq 0 \\ 2 x - y + 4 \geq 0 \end{matrix}$ D、 ${\begin{matrix} 0 \leq y \leq 2 \\ x \leq 0 \\ 2 x - y + 4 \leq 0 \end{matrix}$

查看试题解析
4. 若关于x的不等式 $x^{2} + a x - c < 0$ 的解集为 $\{x | - 2 < x < 1\}$ ，且函数 $y = a x^{3} + m x^{2} + x + \frac{c}{2}$ 在区间 $(\frac{1}{2} ， 1)$ 上不是单调函数，则实数m的取值范围为（）

A、 $(- 3 ， - \sqrt{3})$ B、 $[- 3 ， - \sqrt{3}]$ C、 $(- \infty ， - 2) \cup (\sqrt{3} ， + \infty)$ D、 $(- \infty ， - 2] \cup (- \sqrt{3} ， + \infty)$

查看试题解析
5. 设全集 $U = R$ ，已知集合 $A = \{x | x \geq 1\}$ ， $B = \{x | (x + 2) (x - 1) < 0\}$ ，则（）

A、 $A \cup B = U$ B、 $A \cap B = \emptyset$ C、 $C_{U}^{B} \subseteq A$ D、 $C_{U}^{A} \subseteq B$

查看试题解析
6. 若圆 ${(x - 3)}^{2} + {(y + 5)}^{2} = r^{2}$ 上有且只有两个点到直线 $4 x - 3 y = 2$ 的距离为1，则半径 $r$ 的取值范围（）

A、 $(4 ， 6)$ B、 $[4 ， 6)$ C、 $(4 ， 6]$ D、 $[4 ， 6]$

查看试题解析
7. 下列说法中，正确的是 ( )

A、当x＞0且x≠1时， $l g x + \frac{1}{l g x} \geq 2$ B、当x＞0时， $\sqrt{x} + \frac{1}{\sqrt{x}} \geq 2$ C、当x≥2时， $x + \frac{1}{x}$ 的最小值为2 D、当0＜x≤2时， $x - \frac{1}{x}$ 无最大值

查看试题解析
8. 若不等式组 $\{\begin{matrix} x + y - 2 \leq 0 \\ x + 2 y - 2 \geq 0 \\ x - y + 2 m \geq 0 \end{matrix}$ ，表示的平面区域为三角形，且其面积等于 $\frac{4}{3}$ ，则m的值为（）

A、 $- 3$ B、 $1$ C、 $\frac{4}{3}$ D、 $3$

查看试题解析
9. 设实数x ， y满足 $\{\begin{matrix} 2 x + y \leq 10 \\ x + 2 y \leq 14 \\ x + y \geq 6 \end{matrix}$ ，则xy的最大值为( )

A、 $\frac{25}{2}$ B、 $\frac{49}{2}$ C、12 D、14

查看试题解析
10. 不等式x﹣（m²﹣2m+4）y+6＞0表示的平面区域是以直线x﹣（m²﹣2m+4）y+6=0为界的两个平面区域中的一个，且点（1，1）在这个区域内，则实数m的取值范围是（　　）

A、（﹣∞，﹣1）∪（3，+∞） B、（﹣∞，﹣1]∪[3，+∞） C、[﹣1，3] D、（﹣1，3）

查看试题解析
11. 设a为实常数，y=f（x）是定义在R上的奇函数，当x＞0时，f（x）=4x+ $\frac{1}{x}$ +3，则对于y=f（x）在x＜0时，下列说法正确的是（　　）

A、有最大值7 B、有最大值﹣7 C、有最小值7 D、有最小值﹣7

查看试题解析
12. 设p：实数x，y满足（x﹣1）²+（y﹣1）²≤2，q：实数x，y满足 ${\begin{cases} y \geq x - 1 \\ y \geq 1 - x \\ y \leq 1 \end{cases}$ ，则p是q的（　　）

A、必要不充分条件 B、充分不必要条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
13. 若a＞0，b＞0，且a+b=4，则下列不等式中恒成立的是（　　）

A、 $\frac{1}{a b} > \frac{1}{2}$ B、 $\frac{1}{a} + \frac{1}{b} \leq 1$ C、 $\sqrt{a b} \geq 2$ D、 $\frac{1}{a^{2} + b^{2}} \leq \frac{1}{8}$

查看试题解析
14. 在△ABC中，三顶点分别为A（2，4），B（﹣1，2），C（1，0），点P（x，y）在△ABC内部及其边界上运动，则m=y﹣x的取值范围为（）

A、[1，3] B、[﹣3，1] C、[﹣1，3] D、[﹣3，﹣1]

查看试题解析
15. 关于x的不等式ax²+bx+2＞0的解集为（﹣1，2），则关于x的不等式bx²﹣ax﹣2＞0的解集为（）

A、（﹣2，1） B、（﹣∞，﹣2）∪（1，+∞） C、（﹣∞，﹣1）∪（2，+∞） D、（﹣1，2）

查看试题解析

二、填空题

16. 设集合A={（x，y）| $\{\begin{matrix} 3 x - y + 2 \geq 0 \\ x \leq 4 \\ y \geq 5 \end{matrix}$ }，则区域A的面积为

查看试题解析
17. 若不等式ax²+5x﹣2＞0的解集是 $\{x | \frac{1}{2} < x < 2\}$ ，则不等式ax²+5x+a²﹣1＞0的解集为．

查看试题解析
18. 已知f（x）是定义域为R的偶函数，当x≥0时，f（x）=x²﹣4x，那么，不等式f（x+2）＜5的解集是

查看试题解析
19. 若x，y满足约束条件 $\{\begin{matrix} x - 3 \leq 0 \\ y - 2 \geq 0 \\ y \leq x + 1 \end{matrix}$ ，则目标函数z=﹣2x+y的最小值为

查看试题解析
20. 设x，y满足约束条件 ${\begin{matrix} 3 x - y - 6 \leq 0 \\ x - y + 2 \geq 0 \\ x \geq 0 ， y \geq 0 \end{matrix}$ ，若目标函数z=ax+by（a＞0，b＞0）的值是最大值为12，则 $\frac{2}{a} + \frac{3}{b}$ 的最小值为

查看试题解析

三、综合题

21. 已知f（x）=﹣3x²+a（6﹣a）x+6．

(1)、解关于a的不等式f（1）＞0；

(2)、若不等式f（x）＞b的解集为（﹣1，3），求实数a，b的值．

查看试题解析
22. 一个化肥厂生产甲种混合肥料1车皮、乙种混合肥料1车皮所需要的主要原料如表：
原料
种类
磷酸盐（单位：吨）
硝酸盐（单位：吨）
甲
4
20
乙
2
20
现库存磷酸盐8吨、硝酸盐60吨，计划在此基础上生产若干车皮的甲、乙两种混合肥料．

(1)、设x，y分别表示计划生产甲、乙两种肥料的车皮数，试列出x，y满足的数学关系式，并画出相应的平面区域；

(2)、若生产1车皮甲种肥料，利润为3万元；生产1车皮乙种肥料，利润为2万元．那么分别生产甲、乙两种肥料多少车皮，能够产生最大利润？最大利润是多少？

查看试题解析
23. 已知实数x、y满足 ${\begin{matrix} x - y - 2 \geq 0 \\ x + y - 6 \leq 0 \\ x - 2 y - 2 \leq 0 \end{matrix}$ ，目标函数z=x+ay．

(1)、当a=﹣2时，求目标函数z的取值范围；

(2)、若使目标函数取得最小值的最优解有无数个，求 $\frac{y}{x - a}$ 的最大值．

查看试题解析
24. 设f（x）=（m+1）x²﹣mx+m﹣1．

(1)、当m=1时，求不等式f（x）＞0的解集；

(2)、若不等式f（x）+1＞0的解集为 $(\frac{3}{2} ， 3)$ ，求m的值．

查看试题解析
25. 某人上午7时，乘摩托艇以匀速vkm/h（8≤v≤40）从A港出发到距100km的B港去，然后乘汽车以匀速wkm/h（30≤w≤100）自B港向距300km的C市驶去．应该在同一天下午4至9点到达C市．设乘坐汽车、摩托艇去目的地所需要的时间分别是xh，yh．

(1)、作图表示满足上述条件的x，y范围；

(2)、如果已知所需的经费p=100+3（5﹣x）+2（8﹣y）（元），那么v，w分别是多少时p最小？此时需花费多少元？

查看试题解析