2017高考数学备考复习(理科)专题八:平面向量
试卷更新日期:2017-02-10 类型:一轮复习
一、单选题
-
1. 在平行四边形ABCD中,AC为一条对角线, , 则( )
A、(-2,-4) B、(-3,-5) C、(3,5) D、(2,4)2. 如图,在中,点D是BC边上靠近B的三等分点,则( )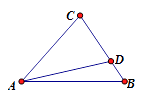 A、 B、 C、 D、3. 已知点 , , 则与共线的单位向量为( )
A、 B、 C、 D、3. 已知点 , , 则与共线的单位向量为( )
A、或 B、 C、或 D、4. 已知、、三点不共线,点为平面外的一点,则下列条件中,能得出平面的条件是( )
A、 B、 C、 D、5. 对于向量a,b,e及实数x,y,x1 , x2 , , 给出下列四个条件:
①且; ②
③且唯一; ④
其中能使a与b共线的是 ( )A、①② B、②④ C、①③ D、③④6. 已知、均为单位向量,它们的夹角为 , 那么( )
A、 B、 C、 D、7. 已知 = , =t若P 点是 所在平面内一点,且 =+ , 则· 的最大值等于( )A、13 B、15 C、19 D、218. 已知向量=(﹣4,3),点A(﹣1,1)和B(0,﹣1)在上的射影分别为A1和B1 , 若= , 则λ的值是( )A、 B、- C、2 D、-29. 设与是不共线的非零向量,且k+与+k共线,则k的值是( )A、1 B、-1 C、±1 D、任意不为零的实数10. 设点A(2,0),B(4,2),若点P在直线AB上,且||=2||,则点P的坐标为( )A、(3,1) B、(1,﹣1) C、(3,1)或(1,﹣1) D、(3,1)或(1,1)11. 已知向量 =( , ), =( , ),则∠ABC=( )A、30° B、45° C、60° D、120°12. 在平面上, ⊥ ,| |=| |=1, = + .若| |< ,则| |的取值范围是( )A、(0, ] B、( , ] C、( , ] D、( , ]13. 在四边形ABCD中, , , ,则四边形ABCD的形状是( )A、长方形 B、平行四边形 C、菱形 D、梯形14. 已知向量 =(1,2), =(0,1), =(﹣2,k),若( +2 )∥ ,则k=( )A、﹣8 B、﹣ C、 D、815. 在△ABC中,内角A= ,P为△ABC的外心,若 =λ1 +2λ2 ,其中λ1与λ2为实数,则λ1+λ2的最大值为( )A、 B、1﹣ C、 D、1+二、填空题
-
16.
已知|
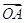 |=|a|=3,|
|=|a|=3,| 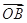 |=|b|=3,∠AOB=90°,则|a+b|=.17. 已知A(﹣1,1),B(1,2),C(﹣2,﹣1),D(3,4),则向量在方向上的投影为18. 若 , 是两个不共线的向量,已知=2+k , =+3 , =2﹣ , 若A,B,D三点共线,则k=19.
|=|b|=3,∠AOB=90°,则|a+b|=.17. 已知A(﹣1,1),B(1,2),C(﹣2,﹣1),D(3,4),则向量在方向上的投影为18. 若 , 是两个不共线的向量,已知=2+k , =+3 , =2﹣ , 若A,B,D三点共线,则k=19.如图,在矩形OABC中,点E,F分别在AB,BC上,且满足AB=3AE,BC=3CF,若=λ+μ(λ,μ∈R),则λ+μ=
 20. 已知向量 =(1, ), =( ,1),则 与 夹角的大小为 .
20. 已知向量 =(1, ), =( ,1),则 与 夹角的大小为 .三、综合题
-
21. 设向量 =(cosθ,sinθ), =(﹣ , );(1)、若 ∥ ,且θ∈(0,π),求θ;(2)、若|3 + |=| ﹣3 |,求| + |的值.22. 已知在平面坐标系内,O为坐标原点,向量 =(1,7), =(5,1), =(2,1),点M为直线OP上的一个动点.(1)、当 • 取最小值时,求向量 的坐标;(2)、在点M满足(I)的条件下,求∠AMB的余弦值.23. 已知 =(cosα,sinα), =(cosβ,sinβ),0<β<α<π.(1)、若| ﹣ |= ,求证: ⊥ ;(2)、设 =(0,1),若 + = ,求α,β的值.24. 已知向量 =(sinx,﹣1), =(2cosx,1).(1)、若 ∥ ,求tanx的值;(2)、若 ⊥ ,又x∈[π,2π],求sinx+cosx的值.25. 如图,A,B,C的坐标分别为(﹣ ,0),( ,0),(m,n),G,O′,H分别为△ABC的重心,外心,垂心.
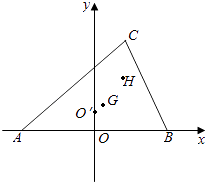 (1)、写出重心G的坐标;(2)、求外心O′,垂心H的坐标;(3)、求证:G,H,O′三点共线,且满足|GH|=2|OG′|.
(1)、写出重心G的坐标;(2)、求外心O′,垂心H的坐标;(3)、求证:G,H,O′三点共线,且满足|GH|=2|OG′|.

