河南省焦作市2018届九年级数学第一次质量抽测试卷
试卷更新日期:2018-07-23 类型:中考模拟
一、单选题
-
1. 在下列各数中,比﹣1小的数是( )A、﹣3 B、﹣ C、0 D、12. 大型纪录电影《厉害了,我的国》3月2日在全国上映,在上映首日收获了4132万人民币的票房。数据“4132万”用科学记数法表示为( )A、 B、 C、 D、3.
用8个相同的小正方体搭成一个几何体,从上面看它得到的平面图形如图所示,那么从左面看它得到的平面图形一定不是( )
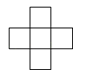 A、
A、 B、
B、 C、
C、 D、
D、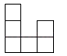 4. 下列计算正确的是( )A、a+b=ab B、 C、a3b÷2ab= a2 D、(-2ab2)3=-6a3b55. 下列关于x的一元二次方程中,有两个相等实数根的是( )A、x2+1=0 B、x2+x﹣1=0 C、x2+2x﹣3=0 D、4x2﹣4x+1=06. 某中学举行书法比赛,各年龄组的参赛人数如下表所示,则全体参赛选手年龄的平均数和中位数分别为( )
4. 下列计算正确的是( )A、a+b=ab B、 C、a3b÷2ab= a2 D、(-2ab2)3=-6a3b55. 下列关于x的一元二次方程中,有两个相等实数根的是( )A、x2+1=0 B、x2+x﹣1=0 C、x2+2x﹣3=0 D、4x2﹣4x+1=06. 某中学举行书法比赛,各年龄组的参赛人数如下表所示,则全体参赛选手年龄的平均数和中位数分别为( )年龄组
13岁
14岁
15岁
16岁
参赛人数
9
15
3
3
A、14.5,14.5 B、14,15 C、14.5,14 D、14,147. 如图,已知在△ABC,AB=AC.若以点B为圆心,BC长为半径画弧,交腰AC于点E,则下列结论一定正确的是( )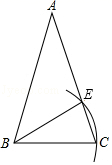 A、AE=EC B、AE=BE C、∠EBC=∠BAC D、∠EBC=∠ABE8. 在一个口袋中有4个完全相同的小球,把它们分别标号为1,2,3,4,随机地摸出一个小球然后放回,再随机地摸出一个小球,则两次摸出的小球的标号之和等于5的概率是( )A、 B、 C、 D、9. 一个寻宝游戏的寻宝通道如图①所示,通道由在同一平面内的AB,BC,CA,OA, OB,OC组成。为记录寻宝者的行进路线,在BC的中点M处放置了一台定位仪器,设寻宝者行进的时间为x,寻宝者与定位仪器之间的距离为y,若寻宝者匀速行进,且表示y与x的函数关系的图像大致如图②所示,则寻宝者的行进路线可能为:( )
A、AE=EC B、AE=BE C、∠EBC=∠BAC D、∠EBC=∠ABE8. 在一个口袋中有4个完全相同的小球,把它们分别标号为1,2,3,4,随机地摸出一个小球然后放回,再随机地摸出一个小球,则两次摸出的小球的标号之和等于5的概率是( )A、 B、 C、 D、9. 一个寻宝游戏的寻宝通道如图①所示,通道由在同一平面内的AB,BC,CA,OA, OB,OC组成。为记录寻宝者的行进路线,在BC的中点M处放置了一台定位仪器,设寻宝者行进的时间为x,寻宝者与定位仪器之间的距离为y,若寻宝者匀速行进,且表示y与x的函数关系的图像大致如图②所示,则寻宝者的行进路线可能为:( ) A、A→O→B B、B→A→C C、B→O→C D、C→B→O10. 如图,AB为半圆O的直径,C为AO的中点,CD⊥AB交半圆于点D,以C为圆心,CD为半径画弧交AB于E点,若AB=4,则图中阴影部分的面积是( )
A、A→O→B B、B→A→C C、B→O→C D、C→B→O10. 如图,AB为半圆O的直径,C为AO的中点,CD⊥AB交半圆于点D,以C为圆心,CD为半径画弧交AB于E点,若AB=4,则图中阴影部分的面积是( )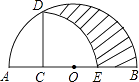 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 计算: = .12. 不等式组 的最大整数解是 .13. 已知反比例函数y= (k≠0)的图象经过点(3,-1),则当1<y<3时,自变量x的取值范围是 .14. 如图,在直角坐标系中,正方形ABCO的点B坐标(3,3),点A、C分别在y轴、x轴上,对角线AC上一动点E,连接BE,过E作DE⊥BE交OC于点D.若点D坐标为(2,0),则点E坐标为 .
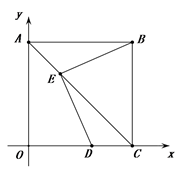 15. 如图,在Rt△ABC中,∠A=90°, ∠B=30°,BC= +1,点E、F分别是BC、AC边上的动点,沿EF所在直线折叠∠C,使点C的对应点C′始终落在边AB上,若△BEC′是直角三角形时,则BC′的长为 .
15. 如图,在Rt△ABC中,∠A=90°, ∠B=30°,BC= +1,点E、F分别是BC、AC边上的动点,沿EF所在直线折叠∠C,使点C的对应点C′始终落在边AB上,若△BEC′是直角三角形时,则BC′的长为 .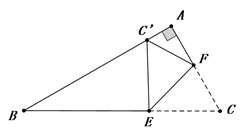
三、解答题
-
16. 化简并求值: ,其中x,y满足|x+2|+(2x+y﹣1)2=0.17. 为了了解学生平均每天“诵读经典”的时间,在全校范围内随机抽查了部分学生进行调查统计,并将调查统计的结果分为:每天诵读时间t ≤20分钟的学生记为A类,20分钟<t ≤40分钟的学生记为B类,40分钟<t ≤60分钟的学生记为C类,t>60分钟的学生记为D类四种.将收集的数据绘制成如下两幅不完整的统计图.
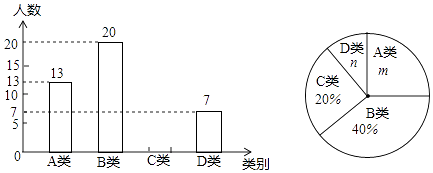
请根据图中提供的信息,解答下列问题:
(1)、这次共抽查了名学生进行调查统计,m=%,n=%;(2)、请补全上面的条形图;(3)、如果该校共有1200名学生,请你估计该校C类学生约有多少人.18. 如图,△ABC内接于⊙O,且AB=AC.延长BC到点D,使CD=CA,连接AD交⊙O于点E. (1)、求证:△ABE≌△CDE;(2)、填空:
(1)、求证:△ABE≌△CDE;(2)、填空:①当∠ABC的度数为时,四边形AOCE是菱形;
②若AE=6,BE=8,则EF的长为.
19. 如图,某校教学楼AB的后面有一建筑物CD,在距离CD的正后方30米的观测点P处,以22°的仰角测得建筑物的顶端C恰好挡住教学楼的顶端A,而在建筑物CD上距离地面3米高的E处,测得教学楼的顶端A的仰角为45°,求教学楼AB的高度.(参考数据:sin22°≈ ,cos22°≈ ,tan22°≈ )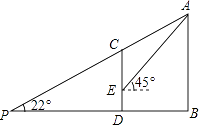 20. 如图,一次函数y=- x+b与反比例函数y= (x>0)的图象交于点A(2,6)和B(m,1)
20. 如图,一次函数y=- x+b与反比例函数y= (x>0)的图象交于点A(2,6)和B(m,1) (1)、填空:一次函数的解析式为 , 反比例函数的解析式为;(2)、点E为y轴上一个动点,若S△AEB=5,求点E的坐标.21. 某文具商店销售功能相同的两种品牌的计算器,购买2个A品牌和1个B品牌的计算器共需122元;购买1个A品牌和2个B品牌的计算器共需124元.
(1)、填空:一次函数的解析式为 , 反比例函数的解析式为;(2)、点E为y轴上一个动点,若S△AEB=5,求点E的坐标.21. 某文具商店销售功能相同的两种品牌的计算器,购买2个A品牌和1个B品牌的计算器共需122元;购买1个A品牌和2个B品牌的计算器共需124元.
(1)、求这两种品牌计算器的单价;(2)、学校开学前夕,该商店举行促销活动,具体办法如下:购买A品牌计算器按原价的九折销售,购买B品牌计算器超出10个以上超出的部分按原价的八折销售,①设购买x个A品牌的计算器需要y1元,购买x个B品牌的计算器需要y2元,分别求出y1、y2关于x的函数关系式;②小明准备联系一部分同学集体购买同一品牌的计算器,若购买计算器的数量超过10个,问购买哪种品牌的计算器更合算?请说明理由.

