河南省高阳县2018届九年级数学中考一模试卷
试卷更新日期:2018-07-23 类型:中考模拟
一、单选题
-
1. 若( ) ,则( )内的数为( )A、 B、 C、 D、2. 将数字21 600用科学记数法表示应为( )A、 B、 C、 D、3. 下列图形中,是轴对称图形,但不是中心对称图形的是( )A、
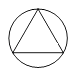 B、
B、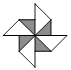 C、
C、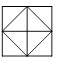 D、
D、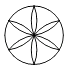 4. 下列计算正确的是( )A、 B、 C、 D、5. 如图,将甲、乙、丙、丁四个小正方形中的一个剪掉,使余下的部分不能围成一个正方体,剪掉的这个小正方形是( )
4. 下列计算正确的是( )A、 B、 C、 D、5. 如图,将甲、乙、丙、丁四个小正方形中的一个剪掉,使余下的部分不能围成一个正方体,剪掉的这个小正方形是( ) A、甲 B、乙 C、丙 D、丁6. 如图,在数轴上表示数 的点可能是( )
A、甲 B、乙 C、丙 D、丁6. 如图,在数轴上表示数 的点可能是( ) A、点E B、点F C、点P D、点Q7. 一组数据:1,3,3,5,若添加一个数据3,则发生变化的统计量是( )A、平均数 B、众数 C、中位数 D、方差8. 计算:1252﹣50×125+252=( )A、100 B、150 C、10000 D、225009. 我国是最早认识负数,并进行相关运算的国家.在古代数学名著《九章算术》里,就记载了利用算筹实施“正负术”的方法,图1表示的是计算3+(-4)的过程.按照这种方法,图2表示的过程应是在计算( )
A、点E B、点F C、点P D、点Q7. 一组数据:1,3,3,5,若添加一个数据3,则发生变化的统计量是( )A、平均数 B、众数 C、中位数 D、方差8. 计算:1252﹣50×125+252=( )A、100 B、150 C、10000 D、225009. 我国是最早认识负数,并进行相关运算的国家.在古代数学名著《九章算术》里,就记载了利用算筹实施“正负术”的方法,图1表示的是计算3+(-4)的过程.按照这种方法,图2表示的过程应是在计算( )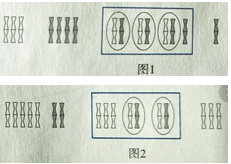 A、(-5)+(-2) B、(-5)+2 C、5+(-2) D、5+210. 将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.点A、B的读数分别为86°、30°,则∠ACB的大小为( )
A、(-5)+(-2) B、(-5)+2 C、5+(-2) D、5+210. 将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.点A、B的读数分别为86°、30°,则∠ACB的大小为( ) A、15 B、28 C、29 D、3411. 已知二元一次方程组 ,如果用加减法消去n,则下列方法可行的是( )A、①×4+②×5 B、①×5+②×4 C、①×5-②×4 D、①×4-②×512. 八年级学生去距学校10km的博物馆参观,一部分学生骑自行车先走,过了20min后,其余学生乘汽车出发,结果他们同时到达,已知汽车的速度是骑车学生速度的2倍,求骑车学生的速度.设骑车学生的速度为
A、15 B、28 C、29 D、3411. 已知二元一次方程组 ,如果用加减法消去n,则下列方法可行的是( )A、①×4+②×5 B、①×5+②×4 C、①×5-②×4 D、①×4-②×512. 八年级学生去距学校10km的博物馆参观,一部分学生骑自行车先走,过了20min后,其余学生乘汽车出发,结果他们同时到达,已知汽车的速度是骑车学生速度的2倍,求骑车学生的速度.设骑车学生的速度为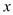 km/h,则所列方程正确的是( )
km/h,则所列方程正确的是( )
A、 B、 C、 D、13. 反比例函数 的图象如图所示,则下列结论正确的是( ) A、常数m<1 B、y随x的增大而增大 C、若A(﹣1,h),B(2,k)在图象上,则h<k D、若P(﹣x,y)在图象上,则P′(x,﹣y)也在图象上14. 已知,如图,△ABC是等边三角形,四边形BDEF是菱形,其中∠E=60°,将菱形BDEF绕点B按顺时针方向旋转,甲、乙两位同学发现在此旋转过程中,有如下结论:
A、常数m<1 B、y随x的增大而增大 C、若A(﹣1,h),B(2,k)在图象上,则h<k D、若P(﹣x,y)在图象上,则P′(x,﹣y)也在图象上14. 已知,如图,△ABC是等边三角形,四边形BDEF是菱形,其中∠E=60°,将菱形BDEF绕点B按顺时针方向旋转,甲、乙两位同学发现在此旋转过程中,有如下结论:甲:线段AF与线段CD的长度总相等;
乙:直线AF和直线CD所夹的锐角的度数不变;
那么,你认为( )
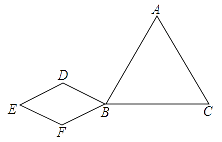 A、甲、乙都对 B、乙对甲不对 C、甲对乙不对 D、甲、乙都不对15. 如图,在Rt△ABC中,∠ACB=90°,D为斜边AB的中点,动点P从B点出发,沿B→C→A运动,如图1所示,设S△DPB=y,点P运动的路程为x,若y与x之间的函数图象如图2所示,则图2中Q点坐标为( )
A、甲、乙都对 B、乙对甲不对 C、甲对乙不对 D、甲、乙都不对15. 如图,在Rt△ABC中,∠ACB=90°,D为斜边AB的中点,动点P从B点出发,沿B→C→A运动,如图1所示,设S△DPB=y,点P运动的路程为x,若y与x之间的函数图象如图2所示,则图2中Q点坐标为( ) A、(4,4) B、(4,3) C、(4,6) D、(4,12)
A、(4,4) B、(4,3) C、(4,6) D、(4,12)二、填空题
-
16. 若|a-1|=2,则a= .17. 如图,在已知的△ABC中,按以下步骤作图:
①分别以B,C为圆心,以大于 BC的长为半径作弧,两弧相交于两点M,N;
②作直线MN交AB于点D,连接CD.
若CD=AC,∠A=50°,则∠ACB= .
 18. 如图,在数轴上,点A表示1,现将点A沿数轴做如下移动:第一次将点A向左移动3个单位长度到达点A1 , 第2次将点A1向右平移6个单位长度到达点A2 , 第3次将点A2向左移动9个单位长度到达点A3…则第6次移动到点A6时,点A6在数轴上对应的实数是;按照这种规律移动下去,第2017次移动到点A2017时,A2017在数轴上对应的实数是 .
18. 如图,在数轴上,点A表示1,现将点A沿数轴做如下移动:第一次将点A向左移动3个单位长度到达点A1 , 第2次将点A1向右平移6个单位长度到达点A2 , 第3次将点A2向左移动9个单位长度到达点A3…则第6次移动到点A6时,点A6在数轴上对应的实数是;按照这种规律移动下去,第2017次移动到点A2017时,A2017在数轴上对应的实数是 .
三、解答题
-
19. 请你阅读小明和小红两名同学的解题过程,并回答所提出的问题.
计算:
问:小明在第几步开始出错,小红在第几步开始出错(写出序号即可);请你给出正确解答过程.
 20. 如图,已知∠MON=25°,矩形ABCD的边BC在OM上,对角线AC⊥ON.
20. 如图,已知∠MON=25°,矩形ABCD的边BC在OM上,对角线AC⊥ON. (1)、求∠ACD度数;(2)、当AC=5时,求AD的长.(参考数据:sin25°=0.42;cos25°=0.91;tan25°=0.47,结果精确到0.1)21. 垫球是排球队常规训练的重要项目之一.下列图表中的数据是甲、乙、丙三人每人十次垫球测试的成绩.测试规则为连续接球10个,每垫球到位1个记1分.
(1)、求∠ACD度数;(2)、当AC=5时,求AD的长.(参考数据:sin25°=0.42;cos25°=0.91;tan25°=0.47,结果精确到0.1)21. 垫球是排球队常规训练的重要项目之一.下列图表中的数据是甲、乙、丙三人每人十次垫球测试的成绩.测试规则为连续接球10个,每垫球到位1个记1分. (1)、写出运动员甲测试成绩的众数为;运动员乙测试成绩的中位数为;运动员丙测试成绩的平均数为;(2)、经计算三人成绩的方差分别为S甲2=0.8、S乙2=0.4、S丙2=0.8,请综合分析,在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人,你认为选谁更合适?为什么?(3)、甲、乙、丙三人相互之间进行垫球练习,每个人的球都等可能的传给其他两人,球最先从甲手中传出,第三轮结束时球回到甲手中的概率是多少?(用树状图或列表法解答)
(1)、写出运动员甲测试成绩的众数为;运动员乙测试成绩的中位数为;运动员丙测试成绩的平均数为;(2)、经计算三人成绩的方差分别为S甲2=0.8、S乙2=0.4、S丙2=0.8,请综合分析,在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人,你认为选谁更合适?为什么?(3)、甲、乙、丙三人相互之间进行垫球练习,每个人的球都等可能的传给其他两人,球最先从甲手中传出,第三轮结束时球回到甲手中的概率是多少?(用树状图或列表法解答)
22. 某校准备组织师生共60人,从甲地乘动车前往乙地参加夏令营活动,动车票价格如表所示:(教师按成人票价购买,学生按学生票价购买).运行区间
成人票价(元/张)
学生票价(元/张)
出发站
终点站
一等座
二等座
二等座
甲地
乙地
26
22
16
若师生均购买二等座票,则共需1020元.
(1)、参加活动的教师和学生各有多少人?
(2)、由于部分教师需提早前往做准备工作,这部分教师均购买一等座票,后续前往的教师和学生均购买二等座票.设提早前往的教师有x人,购买一、二等座票全部费用为y元.①求y关于x的函数关系式;
②若购买一、二等座票全部费用不多于1030元,则提早前往的教师最多只能多少人?
23. 如图①,△ABC中,AC=BC,∠A=30°,点D在AB边上且∠ADC=45°. (1)、求∠BCD的度数;(2)、将图①中的△BCD绕点B顺时针旋转,得到△BC′D′.当点D′恰好落在BC边上时,如图②所示,连接C′C并延长交AB于点E.
(1)、求∠BCD的度数;(2)、将图①中的△BCD绕点B顺时针旋转,得到△BC′D′.当点D′恰好落在BC边上时,如图②所示,连接C′C并延长交AB于点E.①求∠C′CB的度数;
②求证:△C′BD′≌△CAE.
24. 如图,抛物线l:y=﹣x2+bx+c(b,c为常数),其顶点E在正方形ABCD内或边上,已知点A(1,2),B(1,1),C(2,1). (1)、直接写出点D的坐标;(2)、若l经过点B,C,求l的解析式;
(1)、直接写出点D的坐标;(2)、若l经过点B,C,求l的解析式;
(3)、设l与x轴交于点M,N,当l的顶点E与点D重合时,求线段MN的值;当顶点E在正方形ABCD内或边上时,直接写出线段MN的取值范围;
(4)、若l经过正方形ABCD的两个顶点,直接写出所有符合条件的c的值.25. 平面上,Rt△ABC与直径为CE的半圆O如图1摆放,∠B=90°,AC=2CE=m,BC=n,半圆O交BC边于点D,将半圆O绕点C按逆时针方向旋转,点D随半圆O旋转且∠ECD始终等于∠ACB,旋转角记为α(0°≤α≤180°). (1)、当α=0°时,连接DE,则∠CDE=°,CD=;(2)、试判断:旋转过程中 的大小有无变化?请仅就图2的情形给出证明;(3)、若m=10,n=8,当旋转的角度α恰为∠ACB的大小时,求线段BD的长;(4)、若m=6,n= ,当半圆O旋转至与△ABC的边相切时,直接写出线段BD的长.
(1)、当α=0°时,连接DE,则∠CDE=°,CD=;(2)、试判断:旋转过程中 的大小有无变化?请仅就图2的情形给出证明;(3)、若m=10,n=8,当旋转的角度α恰为∠ACB的大小时,求线段BD的长;(4)、若m=6,n= ,当半圆O旋转至与△ABC的边相切时,直接写出线段BD的长.