贵州省遵义市2018届中考数学模拟试卷（五）
试卷更新日期：2018-07-23 类型：中考模拟
一、单选题
-
1. 数轴上的点A到原点的距离是6，则点A表示的数为（ ）A、6或﹣6 B、6 C、﹣6 D、3或﹣32. 已知点A（a，2015）与点A'（﹣2014，b）是关于原点O的对称点，则a+b的值为（ ）
A、1 B、﹣1 C、6 D、43. 若m﹣n=﹣1，则（m﹣n）2﹣2m+2n的值是（ ）A、3 B、2 C、1 D、﹣14. 下列运算正确的是（ ）A、a+2a2=3a3 B、a2•a3=a6 C、（a3）2=a5 D、a6÷a2=a45. 5月14﹣15日“一带一路”论坛峰会在北京隆重召开，促进了我国与世界各国的互联互通互惠，“一带一路”地区覆盖总人数约为44亿人，44亿这个数用科学记数法表示为（ ）A、 4.4×108 B、4.4×109 C、4×109 D、44×1086. 现将背面相同的4张扑克牌背面朝上，洗匀后，从中任意翻开一张是数字4的概率为（ ）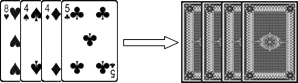
A、 B、 C、 D、7. 观察下列数的特点：0，1，﹣4，9，﹣16，25，…，则第11个数是（ ）
A、﹣121 B、﹣100 C、100 D、1218. 如图，△ABC中，AE交BC于点D，∠C=∠E，AD=4，BC=8，BD：DC=5：3，则DE的长等于（ ）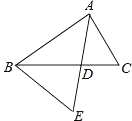
A、 B、 C、 D、9. 如图所示，四边形ABCD是梯形，AD∥BC，CA是∠BCD的平分线，且AB⊥AC，AB=4，AD=6，则tanB=（ ）
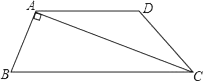A、2 B、2 C、 D、10. 如图，已知双曲线y= （k＜0）经过直角三角形OAB斜边OA的中点D，且与直角边AB相交于点C．若点A的坐标为（﹣6，4），则△AOC的面积为（ ）
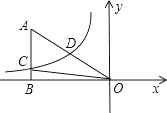A、12 B、9 C、6 D、4二、填空题
-
11. 分解因式：x2+xy= ．12. 若方程x2﹣3x﹣1=0的两根为x1、x2 ， 则 的值为 ．13. 已知2a﹣3b=7，则8+6b﹣4a= ．14. 如图，Rt△ABC的斜边AB=16，Rt△ABC绕点O顺时针旋转后得到Rt△A′B′C′，则Rt△A′B′C′的斜边A′B′上的中线C′D的长度为 ．
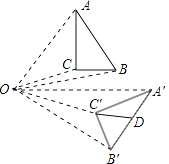15. 如图，直角△ABC中，∠A=90°，∠B=30°，AC=4，以A为圆心，AC长为半径画四分之一圆，则图中阴影部分的面积是（结果保留π）．
16. 如图，在平面直角坐标系中，点O为坐标原点，点P在第一象限，⊙P与x轴交于O，A两点，点A的坐标为（6，0），⊙P的半径为 ，则点P的坐标为 ．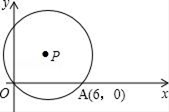
三、解答题
-
17.(1)、计算：（﹣2）﹣1﹣|﹣ |+（ ﹣1）0+cos45°．(2)、已知m2﹣5m﹣14=0，求（m﹣1）（2m﹣1）﹣（m+1）2+1的值．18. 解不等式组 ，并求出它的所有整数解．19. 如图，在矩形ABCD中，连接对角线AC、BD，将△ABC沿BC方向平移，使点B移到点C，得到△DCE．
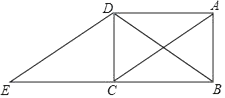(1)、求证：△ACD≌△EDC；(2)、请探究△BDE的形状，并说明理由．20. 某校开展“我最喜爱的一项体育活动”调查，要求每名学生必选且只能选一项，现随机抽查了m名学生，并将其结果绘制成如下不完整的条形图和扇形图．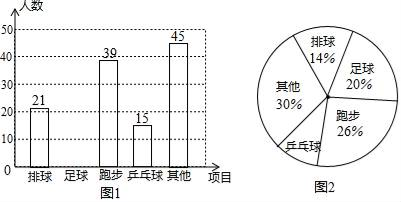
请结合以上信息解答下列问题：
(1)、m=；(2)、请补全上面的条形统计图；(3)、在图2中，“乒乓球”所对应扇形的圆心角的度数为；(4)、已知该校共有1200名学生，请你估计该校约有名学生最喜爱足球活动．21. 如图1，2分别是某款篮球架的实物图与示意图，已知底座BC=0.60米，底座BC与支架AC所成的角∠ACB=75°，支架AF的长为2.50米米，篮板顶端F点到篮框D的距离FD=1.35米，篮板底部支架HF与支架AF所成的角∠FHE=60°，求篮框D到地面的距离（精确到0.01米）.（参考数据：cos75°≈0.2588， sin75°≈0.9659，tan75°≈3.732， ， ）
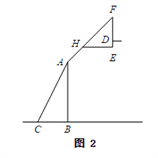22. 学校召集留守儿童过端午节，桌上摆有甲、乙两盘粽子，每盘中盛有白粽2个，豆沙粽1个，肉粽1个（粽子外观完全一样）．(1)、小明从甲盘中任取一个粽子，取到豆沙粽的概率是；(2)、小明在甲盘和乙盘中先后各取了一个粽子，请用树状图或列表法求小明恰好取到两个白粽子的概率．23. 某超市销售一种牛奶，进价为每箱24元，规定售价不低于进价．现在的售价为每箱36元，每月可销售60箱．市场调查发现：若这种牛奶的售价每降价1元，则每月的销量将增加10箱，设每箱牛奶降价x元（x为正整数），每月的销量为y箱．(1)、写出y与x之间的函数关系式和自变量x的取值范围；(2)、超市如何定价，才能使每月销售牛奶的利润最大？最大利润是多少元？24. 如图所示AB为⊙O的一条弦，点C为劣弧AB的中点，E为优弧AB上一点，点F在AE的延长线上，且BE=EF，线段CE交弦AB于点D．
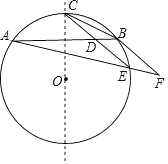(1)、求证：CE∥BF；(2)、若BD=2，且EA：EB：EC=3：1： ，求△BCD的面积（注：根据圆的对称性可知OC⊥AB）．25. 如图，抛物线y=﹣x2+4与x轴交于A、B两点，与y轴交于C点，点P是抛物线上的一个动点且在第一象限，过点P作x轴的垂线，垂足为D，交直线BC于点E．
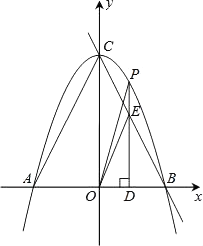(1)、求点A、B、C的坐标和直线BC的解析式；(2)、求△ODE面积的最大值及相应的点E的坐标；
(3)、是否存在以点P、O、D为顶点的三角形与△OAC相似？若存在，请求出点P的坐标，若不存在，请说明理由．