贵州省铜仁市2018届九年级中考数学对点突破模拟试卷

试卷更新日期：2018-07-23 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列说法不正确的是（）

A、0既不是正数，也不是负数 B、绝对值最小的数是0 C、绝对值等于自身的数只有0和1 D、平方等于自身的数只有0和1

查看试题解析
2. 一组数据：3，4，5，x，7的众数是4，则x的值是（　　）

A、3 B、4 C、5 D、6

查看试题解析
3. 下列语句中错误的是（）

A、数字0也是单项式 B、单项式﹣a的系数与次数都是1 C、 $\frac{1}{2}$ xy是二次单项式 D、﹣ $\frac{2}{3} a b$ 的系数是﹣ $\frac{2}{3}$

查看试题解析
4. 如图，已知直线AB，CD被直线AC所截，AB∥CD，E是平面内任意一点（点E不在直线AB，CD，AC上），设∠BAE=α，∠DCE=β．下列各式：①α+β，②α﹣β，③180°﹣α﹣β，④360°﹣α﹣β，∠AEC的度数可能是（）

A、①②③ B、①②④ C、①③④ D、①②③④

查看试题解析
5. 据统计部门发布的信息，广州2016年常驻人口14043500人，数字14043500用科学记数法表示为（）

A、0.140435×10⁸ B、1.40435×10⁷ C、14.0435×10⁶ D、140.435×10⁵

查看试题解析
6. 如图，直线m∥n，圆心在直线n上的⊙A是由⊙B平移得到的，则图中两个阴影三角形的面积大小关系是（）

A、S₁＜S₂ B、S₁=S₂ C、S₁＞S₂ D、不能确定

查看试题解析
7. 如图，在四边形ABCD中，对角线AC平分∠DAB，∠ABD=52°，∠ABC=116°，∠ACB=α°，则∠BDC的度数为（）

A、α B、 $\frac{2}{3} α$ C、90﹣α D、90﹣ $\frac{2}{3} α$

查看试题解析
8. 不等式组 ${\begin{matrix} 2 x - 1 \leq 3 \\ \frac{x}{3} + \frac{1}{2} > \frac{1}{6} \end{matrix}$ 的解集在数轴上表示正确的是（）

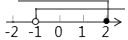A、 B、 C、 D、

查看试题解析
9. 如图，矩形OABC的两边OA、OC在坐标轴上，且OC=2OA，M、N分别为OA、OC的中点，BM与AN交于点E，若四边形EMON的面积为2，则经过点B的双曲线的解析式为（）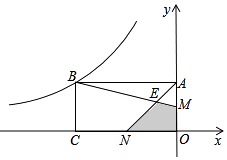

A、y=﹣ $\frac{10}{x}$ B、y=﹣ $\frac{8}{x}$ C、y=﹣ $\frac{6}{x}$ D、y=﹣ $\frac{4}{x}$

查看试题解析
10. 求1+2+2²+2³…+2²⁰¹²的值，可令S=1+2+2²+2³+…+2²⁰¹² ，则2S=2+2²+2³+2⁴+…+2²⁰¹³ ，因此2S﹣S=2²⁰¹³﹣1，仿照以上推理，计算出1+5+5²+5³+…+5²⁰¹⁷的值为（）

A、5²⁰¹⁷﹣1 B、5²⁰¹⁸﹣1 C、 $\frac{5^{2018} - 1}{4}$ D、 $\frac{5^{2017} - 1}{4}$

查看试题解析

二、填空题

11. 当两数时，它们的和为0.

查看试题解析
12. 由小到大排列的一组数据x₁ ， x₂ ， x₃ ， x₄ ， x₅ ，其中每个数据都小于-1，则1，x₁ ， -x₂ ， x₃ ， -x₄ ， x₅的中位数是．

查看试题解析
13. 已知方程x+ $\frac{1}{x} = c + \frac{1}{c}$ （c是常数，c≠0）的解是c或 $\frac{1}{c}$ ，那么方程x+ $\frac{1}{4 x - 6} = \frac{a^{2} + 3 a + 1}{2 a}$ （a是常数，且a≠0）的解是或．

查看试题解析
14. 已知关于x的一元二次方程x²﹣m=2x有两个不相等的实数根，则m的取值范围是．

查看试题解析
15. 如图，在菱形ABCD中，AB=BD，点E，F分别在BC，CD边上，且CE=DF，BF与DE交于点G，若BG=2，DG=4，则CD长为．

查看试题解析
16. 小刚和小明在太阳光下行走，小刚身高1.75米，他的影长为2.0m，小刚比小明矮5cm，此刻小明的影长是 m．

查看试题解析
17. 点P的坐标是（a，b），从﹣2，﹣1，1，2这四个数中任取一个数作为a的值，再从余下的三个数中任取一个数作b的值，则点P（a，b）在平面直角坐标系中第一象限内的概率是．

查看试题解析
18. 如图△ABC中，∠C=90°，AC=8cm，AB的垂直平分线MN交AC于D，连接BD，若cos∠BDC= $\frac{3}{5}$ ，则BC的长为．

查看试题解析

三、解答题

19.

(1)、计算：|﹣2|﹣（π﹣2015）⁰+（ $\frac{1}{2}$ ）^﹣²﹣2sin60°+ $\sqrt{12}$ ；

(2)、先化简，再求值： $\frac{a^{2} - 1}{a^{2} - a}$ ÷（2+ $\frac{a^{2} + 1}{a}$ ），其中a= $\sqrt{2}$ ．

查看试题解析
20. 如图，在△ABC中，AC=8cm，BC=16cm，点P从点A出发，沿着AC边向点C以1cm/s的速度运动，点Q从点C出发，沿着CB边向点B以2cm/s的速度运动，如果P与Q同时出发，经过几秒△PQC和△ABC相似？

查看试题解析
21. 典典同学学完统计知识后，随机调查了她家所在辖区若干名居民的年龄，将调查数据绘制成如下扇形和条形统计图：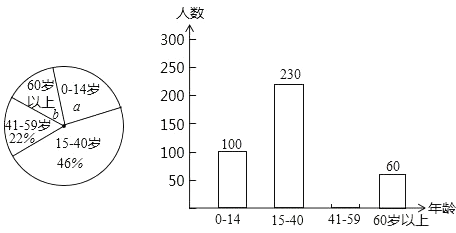
请根据以上不完整的统计图提供的信息，解答下列问题：

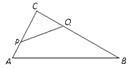
(1)、扇形统计图中a= ， b=；并补全条形统计图；

(2)、若该辖区共有居民3500人，请估计年龄在0～14岁的居民的人数．

(3)、一天，典典知道了辖区内60岁以上的部分老人参加了市级门球比赛，比赛的老人们分成甲、乙两组，典典很想知道甲乙两组的比赛结果，王大爷告诉说，甲组与乙组的得分和为110，甲组得分不低于乙组得分的1.5倍，甲组得分最少为多少？

查看试题解析
22. 在▱ABCD中，E是BC边上一点，F为DE上一点，若∠B=∠AFE，AB=AF．求证：△ADF≌△DEC．

查看试题解析
23. 永定土楼是世界文化遗产“福建土楼”的组成部分，是闽西的旅游胜地．“永定土楼”模型深受游客喜爱．图中折线（AB∥CD∥x轴）反映了某种规格土楼模型的单价y（元）与购买数量x（个）之间的函数关系．

(1)、求当10≤x≤20时，y与x的函数关系式；

(2)、已知某旅游团购买该种规格的土楼模型总金额为2625元，问该旅游团共购买这种土楼模型多少个？（总金额=数量×单价）

查看试题解析
24. 如图，在△ABC中，AB=AC，以AB为直径的⊙O交BC于点D，过点D作DE⊥AC于点E．

(1)、求证：DE是⊙O的切线．

(2)、若∠B=30°，AB=8，求DE的长．

查看试题解析
25. 已知平面直角坐标系中两定点A（﹣1，0）、B（4，0），抛物线y=ax²+bx﹣2（a≠0）过点A，B，顶点为C，点P（m，n）（n＜0）为抛物线上一点．

(1)、求抛物线的解析式和顶点C的坐标；

(2)、当∠APB为钝角时，求m的取值范围；

(3)、若m＞ $\frac{3}{2}$ ，当∠APB为直角时，将该抛物线向左或向右平移t（0＜t＜ $\frac{5}{2}$ ）个单位，点C、P平移后对应的点分别记为C′、P′，是否存在t，使得首位依次连接A、B、P′、C′所构成的多边形的周长最短？若存在，求t的值并说明抛物线平移的方向；若不存在，请说明理由．

查看试题解析