贵州省黔西南州2018届九年级中考数学对点突破模拟试卷（四）

试卷更新日期：2018-07-23 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列各组数中，互为相反数的是（）

A、﹣1与（﹣1）² B、（﹣1）²与1 C、2与 $\frac{1}{2}$ D、2与|﹣2|

查看试题解析
2. 中国京剧脸谱艺术是广大戏曲爱好者非常喜爱的艺术门类，在国内外流行的范围相当广泛，已经被大家公认为是汉民族传统文化的标识之一. 下列脸谱中，属于轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 若一组数据x₁ ， x₂ ， x₃ ， x₄ ， x₅ ， x₆的平均数是2，方差是2，则另一组数据3x₁﹣2，3x₂﹣2，3x₃﹣2，3x₄﹣2，3x₅﹣2，3x₆﹣2的平均数和方差分别是（）

A、2，2 B、2，18 C、4，6 D、4，18

查看试题解析
4. 若x﹣x^﹣1=5，则x²+x^﹣2=（）

A、23 B、24 C、25 D、27

查看试题解析
5. 一个密码锁有五位数字组成，每一位数字都是0，1，2，3，4，5，6，7，8，9之中的一个，小明只记得其中的三个数字，则他一次就能打开锁的概率为（）

A、 $\frac{1}{5}$ B、 $\frac{1}{2}$ C、 $\frac{1}{20}$ D、 $\frac{1}{100}$

查看试题解析
6. 如图， $▱$ ABCD中，E，F分别是AB，CD的中点，则图中有（）个平行四边形．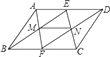

A、7个 B、8个 C、9个 D、10个

查看试题解析
7. 已知⊙O的半径为2，点P是⊙O内一点，且OP= $\sqrt{3}$ ，过P作互相垂直的两条弦AC、BD，则四边形ABCD面积的最大值为（）

A、4 B、5 C、6 D、7

查看试题解析
8. 如图所示，图（1）中含“○”的矩形有1个，图（2）中含“○”的矩形有7个，图（3）中含“○”的矩形有17个，按此规律，图（6）中含“○”的矩形有（）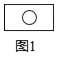

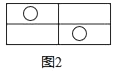
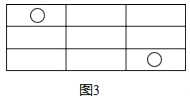A、70 B、71 C、72 D、73

查看试题解析
9. 在函数 $y = \frac{5}{x}$ 的图象上有三点A（﹣2，y₁）、B（﹣1，y₂）、C（2，y₃），则（）

A、y₁＞y₂＞y₃ B、y₃＞y₁＞y₂ C、y₁＞y₃＞y₂ D、y₃＞y₂＞y₁

查看试题解析

二、填空题

10. 去年秋季腮腺炎在某初中流行．若某班某天有2人同时患上腮腺炎，在一天内一人能传染2人，那么经过两天共有人患腮腺炎．

查看试题解析
11. 长城总长约为6 700 010米，用科学记数法表示为米（保留两个有效数字）．

查看试题解析
12. [x]表示不超过x的最大整数．如，[π]=3，[2]=2，[﹣2.1]=﹣3．则下列结论：
①[﹣x]=﹣[x]；②若[x]=n，则x的取值范围是n≤x＜n+1；③当﹣1＜x＜1时，[1+x]+[1﹣x]的值为1或2；④x=﹣2.75是方程4x﹣2[x]+5=0的唯一一个解．其中正确的结论有（写出所有正确结论的序号）．

查看试题解析
13. 已知一组从小到大排列的数据：2，5，x，y，2x，11的平均数与中位数都是7，则这组数据的众数是．

查看试题解析
14. 已知关于x的一元二次方程x²﹣x﹣m=0有两个不相等的实数根，则实数m的取值范围是．

查看试题解析
15. 如图，已知DA∥BC，∠BAC=70°，∠C=40°，则∠DAB=°.

查看试题解析
16. 函数y= $\frac{\sqrt{1 - 2 x}}{x}$ 的自变量x的取值范围是．

查看试题解析
17. 若等腰三角形的两边的边长分别为10cm和5cm，则第三边的长是 cm．

查看试题解析
18. 如图，在正方形ABCD中，对角线AC、BD交于点O，延长CD至点G，使GD= $\frac{1}{3}$ CD，过点D作DE⊥AG，将△ADE沿着AD翻折得到△ADF，连结OF交CD于点H．当CD=3时，求FH的长度为．

查看试题解析
19. 二次函数y=ax²+bx+c（a＜0）的图象与x轴的两个交点A、B的横坐标分别为﹣3、1，与y轴交于点C，下面四个结论：①16a+4b+c＜0；②若P（﹣5，y₁），Q（ $\frac{5}{2}$ ，y₂）是函数图象上的两点，则y₁＞y₂；③c=﹣3a；④若△ABC是等腰三角形，则b=﹣ $\frac{2 \sqrt{7}}{3}$ 或﹣ $\frac{2 \sqrt{15}}{3}$ ．其中正确的有．（请将正确结论的序号全部填在横线上）

查看试题解析

三、解答题

20.

(1)、计算：（ $\sqrt{7}$ ﹣1）⁰﹣（﹣ $\frac{1}{2}$ ）^﹣2+ $\sqrt{3}$ tan30°；

(2)、解方程： $\frac{x + 1}{x - 1} + \frac{4}{1 - x^{2}}$ =1．

查看试题解析
21. 如图，已知AB为⊙O直径，D是 $\overset{⌢}{B C}$ 的中点，DE⊥AC交AC的延长线于E，⊙O的切线交AD的延长线于F．

(1)、求证：直线DE与⊙O相切；

(2)、已知DG⊥AB且DE=4，⊙O的半径为5，求tan∠F的值．

查看试题解析
22. 某学校要制作一批安全工作的宣传材料．甲公司提出：每份材料收费10元，另收1000元的版面设计费；乙公司提出：每份材料收费20元，不收版面设计费．请你帮助该学校选择制作方案．

查看试题解析
23. 已知：如图，AD∥BC，AB=CD，对角线CA平分∠BCD，AD=5，tanB= $\frac{3}{4}$ ，求BC的长．

查看试题解析
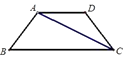24. 如图，在平面直角坐标系xOy中，A、B为x轴上两点，C、D为y轴上的两点，经过点A、C、B的抛物线的一部分c₁与经过点A、D、B的抛物线的一部分c₂组合成一条封闭曲线，我们把这条封闭曲线成为“蛋线”．已知点C的坐标为（0，﹣ $\frac{3}{2}$ ），点M是抛物线C₂：y=mx²﹣2mx﹣3m（m＜0）的顶点．

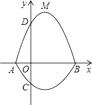(1)、求A、B两点的坐标；

(2)、“蛋线”在第四象限上是否存在一点P，使得△PBC的面积最大？若存在，求出△PBC面积的最大值；若不存在，请说明理由；

(3)、当△BDM为直角三角形时，求m的值．

查看试题解析