贵州省黔西南州2018届九年级中考数学对点突破模拟试卷（二）

试卷更新日期：2018-07-23 类型：中考模拟

进入出卷网下载

一、单选题

1. –2的相反数是（）

A、2 B、 $\frac{1}{2}$ C、–2 D、以上都不对

查看试题解析
2. 已知一组数据：x₁ ， x₂ ， x₃ ， x₄ ， x₅ ， x₆的平均数是2，方差是3，则另一组数据：3x₁﹣2，3x₂﹣2，3x₃﹣2，3x₄﹣2，3x₅﹣2，3x₆﹣2的平均数和方差分别是（）

A、2，3 B、2，9 C、4，25 D、4，27

查看试题解析
3. 如图，下列图形从正面看是三角形的是（）

A、 B、 C、 D、

查看试题解析
4. 若（m+n）²=11，（m﹣n）²=3，则（mn）^﹣2=（）

A、﹣ $\frac{1}{4}$ B、 $\frac{1}{4}$ C、﹣ $\frac{1}{14}$ D、 $\frac{1}{8}$

查看试题解析
5. 从一副扑克牌中随机抽出一张牌，得到梅花或者K的概率是（）

A、 $\frac{17}{52}$ B、 $\frac{8}{27}$ C、 $\frac{17}{54}$ D、 $\frac{16}{52}$

查看试题解析
6. 如图，△ABC中，AB=AC=15，D在BC边上，DE∥BA于点E，DF∥CA交AB于点F，那么四边形AFDE的周长是（）

A、30 B、25 C、20 D、15

查看试题解析
7. 已知⊙O的半径为10，P为⊙O内一点，且OP＝6，则过P点，且长度为整数的弦有（）

A、5条 B、6条 C、8条 D、10条

查看试题解析
8. 如图，下列图形均是完全相同的点按照一定的规律所组成的，第①个图形中一共有3个点，第②个图形中一共有8个点，第③个图形中一共有15个点，…，按此规律排列下去，第9个图形中点的个数是（）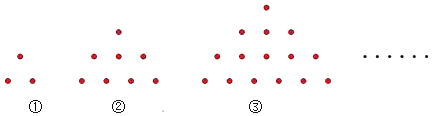

A、80 B、89 C、99 D、109

查看试题解析
9. 如图，两个边长分别为a，b（a＞b）的正方形连在一起，三点C，B，F在同一直线上，反比例函数y= $\frac{k}{x}$ 在第一象限的图象经过小正方形右下顶点E．若OB²﹣BE²=10，则k的值是（）

A、3 B、4 C、5 D、4 $\sqrt{5}$

查看试题解析

二、填空题

10. 大肠杆菌每过20分便由1个分裂成2个，经过3小时后这种大肠杆菌由1个分裂成个．

查看试题解析
11. 据国家考试中心发布的信息，我国今年参加高考的考生数达11600000人，这个数据用科学记数法且保留两个有效数字可表示为人．

查看试题解析
12. 若不等式组 ${\begin{matrix} 2 x - 3 \geq 0 \\ x \leq m \end{matrix}$ 无解，则m的取值范围是．

查看试题解析
13. 若一组数据6，7，5，6，x，1的平均数是5，则这组数据的众数是．

查看试题解析
14. 已知关于x的一元二次方程x²﹣m=2x有两个不相等的实数根，则m的取值范围是．

查看试题解析
15. 如图，AB∥CD，且∠A=25°，∠C=45°，则∠E的度数是．

查看试题解析
16. 已知函数 $y = \sqrt{x - 2}$ ，则x取值范围是．

查看试题解析
17. 已知一个等腰三角形的两边长分别是2和5，那么这个等腰三角形的周长为．

查看试题解析
18. 正方形ABCD中，F是AB上一点，H是BC延长线上一点，连接FH，将△FBH沿FH翻折，使点B的对应点E落在AD上，EH与CD交于点G，连接BG交FH于点M，当GB平分∠CGE时，BM=2 $\sqrt{26}$ ，AE=8，则ED= ．

查看试题解析
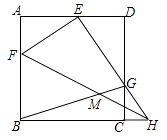19. 二次函数 $y = a x^{2} + b x + c$ （a＜0）图象与x轴的交点A、B的横坐标分别为﹣3，1，与y轴交于点C，下面四个结论：①16a﹣4b+c＜0；②若P（﹣5，y₁），Q（ $\frac{5}{2}$ ，y₂）是函数图象上的两点，则y₁＞y₂；③a=﹣ $\frac{1}{3}$ c；④若△ABC是等腰三角形，则b=﹣ $\frac{2 \sqrt{7}}{3}$ ．其中正确的有（请将结论正确的序号全部填上）

查看试题解析

三、解答题

20.

(1)、计算|﹣ $\sqrt{2}$ |+ $\sqrt{9}$ ×（ $\frac{1}{2}$ ）^﹣1﹣2cos45°﹣（π﹣1）⁰

(2)、解分式方程： $\frac{1}{x - 2}$ ﹣3= $\frac{x - 1}{2 - x}$

查看试题解析
21. 如图，已知，AB是⊙O的直径，点P在AB的延长线上，弦CE交AB于点D，连结OE，AC，且∠P=∠E，∠POE=2∠CAB．

(1)、求证：CE⊥AB；

(2)、求证：PC是⊙O的切线；

(3)、若BD=2OD，且PB=9，求⊙O的半径长和tan∠P的值．

查看试题解析
22. 抚顺某中学为了解八年级学生的体能状况，从八年级学生中随机抽取部分学生进行体能测试，测试结果分为A，B，C，D四个等级．请根据两幅统计图中的信息回答下列问题：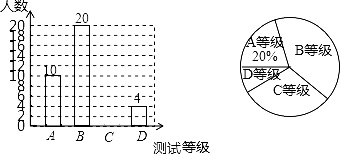

(1)、本次抽样调查共抽取了多少名学生？

(2)、求测试结果为C等级的学生数，并补全条形图；

(3)、若该中学八年级共有700名学生，请你估计该中学八年级学生中体能测试结果为D等级的学生有多少名？

(4)、若从体能为A等级的2名男生2名女生中随机的抽取2名学生，做为该校培养运动员的重点对象，请用列表法或画树状图的方法求所抽取的两人恰好都是男生的概率．

查看试题解析
23. A、B两辆汽车同时从相距330千米的甲、乙两地相向而行，s（千米）表示汽车与甲地的距离，t（分）表示汽车行驶的时间，如图，L₁ ， L₂分别表示两辆汽车的s与t的关系？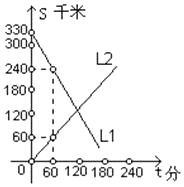

(1)、L₁表示哪辆汽车到甲地的距离与行驶时间的关系？

(2)、汽车B的速度是多少？

(3)、求L₁ ， L₂分别表示的两辆汽车的s与t的关系式．

(4)、2小时后，两车相距多少千米？

(5)、行驶多长时间后，A、B两车相遇？

查看试题解析
24. 如图，ABCD为正方形，E为BC上一点，将正方形折叠，使A点与E点重合，折痕为MN，若tan∠AEN= $\frac{1}{3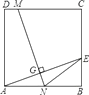}$ ，DC+CE=10．

(1)、求△ANE的面积；

(2)、求sin∠ENB的值．

查看试题解析
25. 已知，抛物线y=ax²+ax+b（a≠0）与直线y=2x+m有一个公共点M（1，0），且a＜b．

(1)、求b与a的关系式和抛物线的顶点D坐标（用a的代数式表示）；

(2)、直线与抛物线的另外一个交点记为N，求△DMN的面积与a的关系式；

(3)、a=﹣1时，直线y=﹣2x与抛物线在第二象限交于点G，点G、H关于原点对称，现将线段GH沿y轴向上平移t个单位（t＞0），若线段GH与抛物线有两个不同的公共点，试求t的取值范围．

查看试题解析