贵州省毕节市2018届九年级中考数学全真模拟试卷（二）

试卷更新日期：2018-07-23 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列实数中是无理数的是（）

A、0.38 B、 $\sqrt{4}$ C、﹣ $\frac{22}{7}$ D、π

查看试题解析
2. 一方有难、八方支援，截至5月26日12时，徐州巿累计为汶川地震灾区捐款约为11 180万元，该笔善款可用科学记数法表示为（）

A、11.18×10³万元 B、1.118×10⁴万元 C、1.118×10⁵万元 D、1.118×10⁸万元

查看试题解析
3. 下列计算正确的是（）

A、a²•a³=a⁶ B、a⁶÷a³=a² C、（﹣2a²）³=﹣8a⁶ D、4x³﹣3x²=1

查看试题解析
4. 如图是一个包装纸盒的三视图（单位：cm），则制作一个纸盒所需纸板的面积是（）

A、75（1+ $\sqrt{3}$ ）cm² B、75（1+ $\frac{1}{2}$ $\sqrt{3}$ ）cm² C、75（2+ $\sqrt{3}$ ）cm² D、75（2+ $\frac{1}{2}$ $\sqrt{3}$ ）cm²

查看试题解析
5. 数学老师给出如下数据1，2，2，3，2，关于这组数据的正确说法是（）

A、众数是2 B、极差是3 C、中位数是1 D、平均数是4

查看试题解析
6. 如图，AB∥CD，∠ABK的角平分线BE的反向延长线和∠DCK的角平分线CF的反向延长线交于点H，∠K﹣∠H=27°，则∠K=（）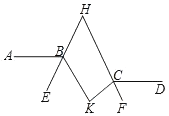

A、76° B、78° C、80° D、82°

查看试题解析
7. 不等式组 ${\begin{matrix} x \geq - 5 \\ x > - 5 \frac{1}{2} \end{matrix}$ 的解集是（）

A、x＞ $- 5 \frac{1}{2}$ B、x＞﹣5 C、 $- 5 \frac{1}{2}$ ＜x＜﹣5 D、x≥﹣5

查看试题解析
8. 为了解某市初中生视力情况，有关部门进行了一次抽样调查，数据如下表，若该市共有初中生15万人，则全市视力不良的初中生的人数大约是（）

A、2160人 B、7.2万人 C、7.8万人 D、4500人

查看试题解析
9. 若关于x的分式方程 $\frac{x + m}{x - 2} + \frac{2 m}{2 - x} = 3$ 有增根，则m的值为（）

A、﹣2 B、0 C、1 D、2

查看试题解析
10. 若一组数据x₁ ， x₂ ， x₃ ， x₄ ， x₅ ， x₆的平均数是2，方差是2，则另一组数据3x₁﹣2，3x₂﹣2，3x₃﹣2，3x₄﹣2，3x₅﹣2，3x₆﹣2的平均数和方差分别是（）

A、2，2 B、2，18 C、4，6 D、4，18

查看试题解析
11. 在平面直角坐标系中，把直线y=2x向左平移1个单位长度，平移后的直线解析式是（）

A、y=2x+1 B、y=2x﹣1 C、y=2x+2 D、y=2x﹣2

查看试题解析
12. 如图，四边形ABCD内接于⊙O，它的对角线把四个内角分成八个角，其中相等的角有（）

A、2对 B、4对 C、6对 D、8对

查看试题解析
13. 如图，Rt△ABC中，∠ACB=90°，斜边AB=9，D为AB的中点，F为CD上一点，且CF= $\frac{1}{3}$ CD，过点B作BE∥DC交AF的延长线于点E，则BE的长为（）

A、6 B、4 C、7 D、12

查看试题解析
14. 如图，将30°的直角三角尺ABC绕直角顶点A逆时针旋转到ADE的位置，使B点的对应点D落在BC边上，连接EB，EC，则下列结论：①∠DAC=∠DCA；②ED为AC的垂直平分线；③∠BED=30°；④ED=2AB．其中正确的是（）

A、①②③ B、①②④ C、②③④ D、①②③④

查看试题解析
15. 如图，MN是等边三角形ABC的一条对称轴，D为AC的中点，点P是直线MN上的一个动点，当PC+PD最小时，∠PCD的度数是（）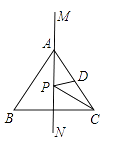

A、30° B、15° C、20° D、35°

查看试题解析

二、填空题

16. 分解因式：3x²﹣6x²y+3xy²= ．

查看试题解析
17. 如图，把正六边形各边按同一方向延长，使延长的线段与原正六边形的边长相等，顺次连接这六条线段外端点可以得到一个新的正六边形，重复上述过程，经过10次后，所得到的正六边形是原正六边形边长的倍．

查看试题解析
18. 如图所示，直线y= $\frac{1}{2}$ x分别与双曲线y= $\frac{k_{1}}{x}$ （k₁＞0，x＞0）、双曲线y= $\frac{k_{2}}{x}$ （k₂＞0，x＞0）交于点A，点B，且OA=2AB，将直线向左平移4个单位长度后，与双曲线y= $\frac{k_{2}}{x}$ 交于点C，若S_△_ABC=1，则k₁k₂的值为．

查看试题解析
19. 记录某足球队全年比赛结果（“胜”、“负”、“平”）的条形统计图和扇形统计图（不完整）如下：
根据图中信息，该足球队全年比赛胜了场．

查看试题解析
20. 将正整数按如图所示的规律排列下去，若用有序数对（m，n）表示从上到下第m排，从左到右第n个数，如（4，2）表示整数8．则（62，55）表示的数是．

查看试题解析

三、解答题

21. 计算：（π+ $\sqrt{3}$ ）⁰+ $\sqrt{12}$ ﹣2sin60°﹣（ $\frac{1}{2}$ ）^﹣² ．

查看试题解析
22. 已知：ax=by=cz=1，求 $\frac{1}{1 + a^{4}} + \frac{1}{1 + b^{4}} + \frac{1}{1 + c^{4}} + \frac{1}{1 + x^{4}} + \frac{1}{1 + y^{4}} + \frac{1}{1 + z^{4}}$ 的值．

查看试题解析
23. 小明、小华用除了正面的数字不同其他完全相同的4张卡片玩游戏，卡片上的数字分别是2、4、5、6，他俩将卡片洗匀后，背面朝上放置在桌面上，小明先抽，小华后抽，抽出的卡片不放回

(1)、若小明恰好抽到了标注4的卡片，直接写出小华抽出的卡片上的数字比4大的概率是多少；

(2)、小明、小华约定，若小明抽到的卡片的标注数字比小华的大，则小明胜：反之，则小明负，你认为这个游戏是否公平？请用树状图或列表法说明理由．

查看试题解析
24. 如图，在▱ABCD中过点A作AE⊥DC，垂足为E，连接BE，F为BE上一点，且∠AFE=∠D．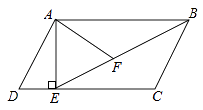

(1)、求证：△ABF∽△BEC；

(2)、若AD=5，AB=8，sinD= $\frac{4}{5}$ ，求AF的长．

查看试题解析
25.

(1)、又一个“六一”国际儿童节即将到来，学校打算给初一的学生赠送精美文具包，文具店规定一次购买400个以上，可享受8折优惠．若给初一学生每人购买一个，则不能享受优惠，需付款1936元；若多买88个，则可享受优惠，同样只需付款1936元，该校初一年级学生共有多少人？

(2)、初一（1）班为准备六一联欢会，欲购买价格分别为4元、8元和20元的三种奖品，每种奖品至少购买一件，共买16件，恰好用100元．若4元的奖品购买a件，先用含a的代数式表示另外两种奖品的件数，然后设计可行的购买方案．
作为初二的大哥哥、大姐姐，你会解决这两个问题吗？

查看试题解析
26. 如图，平行四边形ABCD中，以A为圆心，AB为半径的圆交AD于F，交BC于G，延长BA交圆于E．

(1)、若ED与⊙A相切，试判断GD与⊙A的位置关系，并证明你的结论；

(2)、在（1）的条件不变的情况下，若GC=CD，求∠C．

查看试题解析
27. 综合与探究：
如图，抛物线y= $\frac{1}{4}$ x²﹣ $\frac{3}{2}$ x﹣4与x轴交与A，B两点（点B在点A的右侧），与y轴交于点C，连接BC，以BC为一边，点O为对称中心作菱形BDEC，点P是x轴上的一个动点，设点P的坐标为（m，0），过点P作x轴的垂线l交抛物线于点Q．

(1)、求点A，B，C的坐标．

(2)、当点P在线段OB上运动时，直线l分别交BD，BC于点M，N．试探究m为何值时，四边形CQMD是平行四边形，此时，请判断四边形CQBM的形状，并说明理由．

(3)、当点P在线段EB上运动时，是否存在点Q，使△BDQ为直角三角形？若存在，请直接写出点Q的坐标；若不存在，请说明理由．

查看试题解析