广西南宁市2018届九年级中考数学全真模拟试卷(一)
试卷更新日期:2018-07-23 类型:中考模拟
一、单选题
-
1. 如图,下列图形从正面看是三角形的是( )A、
 B、
B、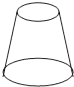 C、
C、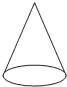 D、
D、 2. 据悉,超级磁力风力发电机可以大幅度提升风力发电效率,但其造价高昂,每座磁力风力发电机,其建造花费估计要5 300万美元,“5 300万”用科学记数法可表示为( )A、5.3×103 B、5.3×104 C、5.3×107 D、5.3×1083. 若将代数式中的任意两个字母互相替换,代数式不变,则称这个代数式为完全对称式、如在代数式a+b+c中,把a和b互相替换,得b+a+c;把a和c互相替换,得c+b+a;把b和c…;a+b+c就是完全对称式、下列三个代数式:①(a﹣b)2;②ab+bc+ca;③a2b+b2c+c2a其中为完全对称式的是( )
2. 据悉,超级磁力风力发电机可以大幅度提升风力发电效率,但其造价高昂,每座磁力风力发电机,其建造花费估计要5 300万美元,“5 300万”用科学记数法可表示为( )A、5.3×103 B、5.3×104 C、5.3×107 D、5.3×1083. 若将代数式中的任意两个字母互相替换,代数式不变,则称这个代数式为完全对称式、如在代数式a+b+c中,把a和b互相替换,得b+a+c;把a和c互相替换,得c+b+a;把b和c…;a+b+c就是完全对称式、下列三个代数式:①(a﹣b)2;②ab+bc+ca;③a2b+b2c+c2a其中为完全对称式的是( )
A、①② B、②③ C、①③ D、①②③4. 不等式组 的解集在数轴上表示正确的是( )A、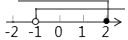 B、
B、 C、
C、 D、
D、 5. 2015年5月31日,我国飞人苏炳添在美国尤金举行的国际田联钻石联赛100米男子比赛中,获得好成绩,成为历史上首位突破10秒大关的黄种人,如表是苏炳添近五次大赛参赛情况:则苏炳添这五次比赛成绩的众数和中位数分别为( )
5. 2015年5月31日,我国飞人苏炳添在美国尤金举行的国际田联钻石联赛100米男子比赛中,获得好成绩,成为历史上首位突破10秒大关的黄种人,如表是苏炳添近五次大赛参赛情况:则苏炳添这五次比赛成绩的众数和中位数分别为( )比赛日期
2012﹣8﹣4
2013﹣5﹣21
2014﹣9﹣28
2015﹣5﹣20
2015﹣5﹣31
比赛地点
英国伦敦
中国北京
韩国仁川
中国北京
美国尤金
成绩(秒)
10.19
10.06
10.10
10.06
9.99
A、10.06秒,10.06秒 B、10.10秒,10.06秒 C、10.06秒,10.10秒 D、10.08秒,10.06秒6. 如图,用直尺和三角尺画图:已知点P和直线a,经过点P作直线b,使b∥a,其画法的依据是( )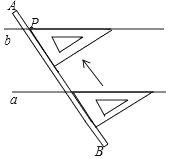 A、同位角相等,两直线平行 B、两直线平行,同位角相等 C、过直线外一点有且只有一条直线与已知直线平行 D、内错角相等,两直线平行7. 不透明的袋子里装有2个红球和1个白球,这些球除了颜色外其他都相同.从中任意摸出一个球,记下颜色后,放回摇匀,再从中摸出一个,则两次摸到球的颜色相同的概率是( )A、 B、 C、 D、8. 如图,⊙O的半径为6,四边形内接于⊙O,连结OA,OC,若∠AOC=∠ABC,则劣弧AC的长为( )
A、同位角相等,两直线平行 B、两直线平行,同位角相等 C、过直线外一点有且只有一条直线与已知直线平行 D、内错角相等,两直线平行7. 不透明的袋子里装有2个红球和1个白球,这些球除了颜色外其他都相同.从中任意摸出一个球,记下颜色后,放回摇匀,再从中摸出一个,则两次摸到球的颜色相同的概率是( )A、 B、 C、 D、8. 如图,⊙O的半径为6,四边形内接于⊙O,连结OA,OC,若∠AOC=∠ABC,则劣弧AC的长为( ) A、 B、2π C、4π D、6π9. 在今年抗震赈灾活动中,小明统计了自己所在学校的甲、乙两班的捐款情况,得到三个信息:(1)甲班捐款2500元,乙班捐款2700元;(2)乙班平均每人捐款数比甲班平均每人捐款数多 ;(3)甲班比乙班多5人,设甲班有x人,根据以上信息列方程得( )
A、 B、2π C、4π D、6π9. 在今年抗震赈灾活动中,小明统计了自己所在学校的甲、乙两班的捐款情况,得到三个信息:(1)甲班捐款2500元,乙班捐款2700元;(2)乙班平均每人捐款数比甲班平均每人捐款数多 ;(3)甲班比乙班多5人,设甲班有x人,根据以上信息列方程得( )
A、 B、 C、 D、10. 如图,一艘海轮位于灯塔P的南偏东45°方向,距离灯塔30海里的A处,它沿正北方向航行一段时间后,到达位于灯塔P的北偏东30°方向上的B处,这时,B处于灯塔P的距离为( ) A、30 海里 B、15 海里 C、30 海里 D、15 海里11. 对于二次函数y=x2+mx+1,当0<x≤2时的函数值总是非负数,则实数m的取值范围为( )
A、30 海里 B、15 海里 C、30 海里 D、15 海里11. 对于二次函数y=x2+mx+1,当0<x≤2时的函数值总是非负数,则实数m的取值范围为( )
A、m≥﹣2 B、﹣4≤m≤﹣2 C、m≥﹣4 D、m≤﹣4或m≥﹣2二、填空题
-
12. 绝对值是5的有理数是 .13. 李好在六月月连续几天同一时刻观察电表显示的度数,记录如下:
日期
1号
2号
3号
4号
5号
6号
7号
8号
…
30号
电表显示(度)
120
123
127
132
138
141
145
148
…
估计李好家六月份总月电量是。
14. 若关于x,y方程组 的解为 ,则方程组 的解为 .15. 如图,在边长为2的菱形ABCD中,∠D=60°,点E、F分别在边AB、BC上.将△BEF沿着直线EF翻折,点B恰好与边AD的中点G重合,则BE的长等于 16. 如果反比例函数y= (k≠0)的图象在每个象限内,y随着x的增大而减小,那么请你写出一个满足条件的反比例函数解析式(只需写一个).
16. 如果反比例函数y= (k≠0)的图象在每个象限内,y随着x的增大而减小,那么请你写出一个满足条件的反比例函数解析式(只需写一个).
17. 如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A( ,0),B(0,2),则B2的坐标为点B2016的坐标为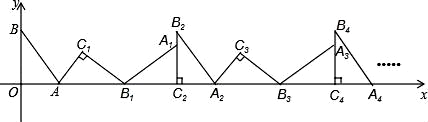
三、解答题
-
18. 计算:( ﹣1)2+3tan30°﹣( ﹣2)( +2)+2sin60°.19. (y﹣z)2+(x﹣y)2+(z﹣x)2=(y+z﹣2x)2+(z+x﹣2y)2+(x+y﹣2z)2 .
求 的值.
20. 如图,点A、B、C的坐标分别为(﹣3,1)、(﹣4,﹣1)、(﹣1,﹣1),将△ABC先向下平移2个单位,得△A1B1C1;再将△A1B1C1沿y轴翻折180°,得△A2B2C2;. (1)、画出△A1B1C1和△A2B2C2;
(1)、画出△A1B1C1和△A2B2C2;
(2)、求直线A2A的解析式.21. 已知四边形ABCD是矩形,连接AC,点E是边CB延长线上一点,CA=CE,连接AE,F是线段AE的中点,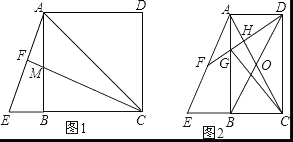 (1)、如图1,当AD=DC时,连接CF交AB于M,求证:BM=BE;
(1)、如图1,当AD=DC时,连接CF交AB于M,求证:BM=BE;
(2)、如图2,连接BD交AC于O,连接DF分别交AB、AC于G、H,连接GC,若∠FDB=30°,S四边形GBOH= ,求线段GC的长.
22. 某学校计划开设四门选修课:乐器、舞蹈、绘画、书法.为提前了解学生的选修情况,学校采取随机抽样的方法进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门).对调查结果进行了整理,绘制成如下两幅不完整的统计图,请结合图中所给信息解答下列问题: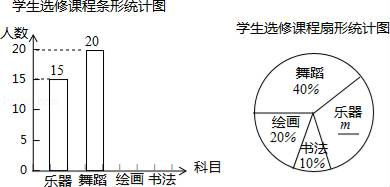 (1)、本次调查的学生共有人,在扇形统计图中,m的值是;(2)、将条形统计图补充完整;(3)、在被调查的学生中,选修书法的有2名女同学,其余为男同学,现要从中随机抽取2名同学代表学校参加某社区组织的书法活动,请直接写出所抽取的2名同学恰好是1名男同学和1名女同学的概率.23. 今年奉节脐橙喜获丰收,某村委会将全村农户的脐橙统一装箱出售.经核算,每箱成本为40元,统一零售价定为每箱50元,可以根据买家订货量的多少给出不同的折扣价销售.(1)、问最多打几折销售,才能保证每箱脐橙的利润率不低于10%?(2)、该村最开始几天每天可卖5000箱,因脐橙的保鲜周期短,需要尽快打开销路,减少积压,村委会决定在零售价基础上每箱降价3m%,这样每天可多销售 m%;为了保护农户的收益与种植积极性,政府用“精准扶贫基金”给该村按每箱脐橙m元给予补贴进行奖励,结果该村每天脐橙销售的利润为49000元,求m的值.24. 如图,矩形ABCD中,AB=4,BC=6,E是BC边的中点,点P在线段AD上,过P作PF⊥AE于F,设PA=x.
(1)、本次调查的学生共有人,在扇形统计图中,m的值是;(2)、将条形统计图补充完整;(3)、在被调查的学生中,选修书法的有2名女同学,其余为男同学,现要从中随机抽取2名同学代表学校参加某社区组织的书法活动,请直接写出所抽取的2名同学恰好是1名男同学和1名女同学的概率.23. 今年奉节脐橙喜获丰收,某村委会将全村农户的脐橙统一装箱出售.经核算,每箱成本为40元,统一零售价定为每箱50元,可以根据买家订货量的多少给出不同的折扣价销售.(1)、问最多打几折销售,才能保证每箱脐橙的利润率不低于10%?(2)、该村最开始几天每天可卖5000箱,因脐橙的保鲜周期短,需要尽快打开销路,减少积压,村委会决定在零售价基础上每箱降价3m%,这样每天可多销售 m%;为了保护农户的收益与种植积极性,政府用“精准扶贫基金”给该村按每箱脐橙m元给予补贴进行奖励,结果该村每天脐橙销售的利润为49000元,求m的值.24. 如图,矩形ABCD中,AB=4,BC=6,E是BC边的中点,点P在线段AD上,过P作PF⊥AE于F,设PA=x.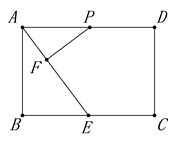
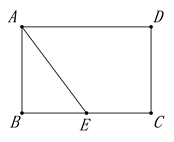 (1)、求证:△PFA∽△ABE;
(1)、求证:△PFA∽△ABE;
(2)、当点P在线段AD上运动时,设PA=x,是否存在实数x,使得以点P,F,E为顶点的三角形也与△ABE相似?若存在,请求出x的值;若不存在,请说明理由;
(3)、探究:当以D为圆心,DP为半径的⊙D与线段AE只有一个公共点时,请直接写出x满足的条件: .25. 已知,抛物线y=ax2+ax+b(a≠0)与直线y=2x+m有一个公共点M(1,0),且a<b. (1)、求b与a的关系式和抛物线的顶点D坐标(用a的代数式表示);
(1)、求b与a的关系式和抛物线的顶点D坐标(用a的代数式表示);
(2)、直线与抛物线的另外一个交点记为N,求△DMN的面积与a的关系式;
(3)、a=﹣1时,直线y=﹣2x与抛物线在第二象限交于点G,点G、H关于原点对称,现将线段GH沿y轴向上平移t个单位(t>0),若线段GH与抛物线有两个不同的公共点,试求t的取值范围.