广西南宁市2018届九年级中考数学全真模拟试卷(二)
试卷更新日期:2018-07-23 类型:中考模拟
一、单选题
-
1. 已知△ABC的三个内角为A,B,C且α=A+B,β=C+A,γ=C+B,则α,β,γ中,锐角的个数最多为( )
A、1 B、2 C、3 D、02. 如图2的三幅图分别是从不同方向看图1所示的工件立体图得到的平面图形,(不考虑尺寸)其中正确的是( )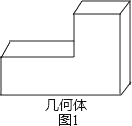
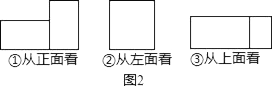 A、①② B、①③ C、②③ D、③3. 我国“神七”在2008年9月26日顺利升空,宇航员在27日下午4点30分在距离地球表面423公里的太空中完成了太空行走,这是我国航天事业的又一历史性时刻.将423公里用科学记数法表示应为( )米.A、42.3×104 B、4.23×102 C、4.23×105 D、4.23×1064. 若将代数式中的任意两个字母交换,代数式不变,则称这个代数式为完全对称式,如a+b+c就是完全对称式.下列三个代数式:①(a﹣b)2;②ab+bc+ca;③a2b+b2c+c2a.其中是完全对称式的是( )A、①②③ B、①③ C、②③ D、①②5. 一元一次不等式组 的解集在数轴上表示正确的是( )A、
A、①② B、①③ C、②③ D、③3. 我国“神七”在2008年9月26日顺利升空,宇航员在27日下午4点30分在距离地球表面423公里的太空中完成了太空行走,这是我国航天事业的又一历史性时刻.将423公里用科学记数法表示应为( )米.A、42.3×104 B、4.23×102 C、4.23×105 D、4.23×1064. 若将代数式中的任意两个字母交换,代数式不变,则称这个代数式为完全对称式,如a+b+c就是完全对称式.下列三个代数式:①(a﹣b)2;②ab+bc+ca;③a2b+b2c+c2a.其中是完全对称式的是( )A、①②③ B、①③ C、②③ D、①②5. 一元一次不等式组 的解集在数轴上表示正确的是( )A、 B、
B、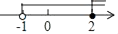 C、
C、 D、
D、 6. 为了分析某班在四月调考中的数学成绩,对该班所有学生的成绩分数换算成等级统计结果如图所示,
6. 为了分析某班在四月调考中的数学成绩,对该班所有学生的成绩分数换算成等级统计结果如图所示,
, 下列说法:①该班B等及B等以上占全班60% ②D等有4人,没有得满分的(按120分制) ③成绩分数(按120分制)的中位数在第三组 ④成绩分数(按120分制)的众数在第三组,其中正确的是( )
A、①② B、③④ C、①③ D、①③④7. 如图,给出了过直线AB外一点P,作已知直线AB的平行线的方法,其依据是( ) A、同位角相等,两直线平行 B、内错角相等,两直线平行 C、同旁内角互补,两直线品行 D、过直线外一点有且只有一条直线与这条直线平行8. 一枚质地均匀的正方体骰子的六个面上的数字分别是1,2,3,4,5,6.掷两次骰子,设其朝上的面上的两个数字之和除以4的余数分别是0,1,2,3的概率为P0 , P1 , P2 , P3 , 则P0 , P1 , P2 , P3中最大的是( )A、P0 B、P1 C、P2 D、P39. 已知圆O的半径是3,A,B,C 三点在圆O上,∠ACB=60°,则弧AB的长是( )A、2π B、π C、 π D、 π10. 为响应 “绿色校园”的号召,八年级(5)班全体师生义务植树300棵.原计划每小时植树 棵,但由于参加植树的全体师生植树的积极性高涨,实际工作效率提高为原计划的1.2倍,结果提前20分钟完成任务.则下面所列方程中,正确的是( )
A、同位角相等,两直线平行 B、内错角相等,两直线平行 C、同旁内角互补,两直线品行 D、过直线外一点有且只有一条直线与这条直线平行8. 一枚质地均匀的正方体骰子的六个面上的数字分别是1,2,3,4,5,6.掷两次骰子,设其朝上的面上的两个数字之和除以4的余数分别是0,1,2,3的概率为P0 , P1 , P2 , P3 , 则P0 , P1 , P2 , P3中最大的是( )A、P0 B、P1 C、P2 D、P39. 已知圆O的半径是3,A,B,C 三点在圆O上,∠ACB=60°,则弧AB的长是( )A、2π B、π C、 π D、 π10. 为响应 “绿色校园”的号召,八年级(5)班全体师生义务植树300棵.原计划每小时植树 棵,但由于参加植树的全体师生植树的积极性高涨,实际工作效率提高为原计划的1.2倍,结果提前20分钟完成任务.则下面所列方程中,正确的是( )
A、 B、 C、 D、11. 上午9时,一条船从A处出发,以每小时40海里的速度向正东方向航行,9时30分到达B处(如图).从A,B两处分别测得小岛M在北偏东45°和北偏东15°方向,那么在B处船与小岛M的距离为( ) A、20海里 B、20 海里 C、10 海里 D、20 海里12. 已知函数y=x2﹣2mx+2016(m为常数)的图象上有三点:A(x1 , y1),B(x2 , y2),C(x3 , y3),其中x1=﹣ +m,x2= +m,x3=m﹣1,则y1、y2、y3的大小关系是( )A、y1<y3<y2 B、y3<y1<y2 C、y1<y2<y3 D、y2<y3<y1
A、20海里 B、20 海里 C、10 海里 D、20 海里12. 已知函数y=x2﹣2mx+2016(m为常数)的图象上有三点:A(x1 , y1),B(x2 , y2),C(x3 , y3),其中x1=﹣ +m,x2= +m,x3=m﹣1,则y1、y2、y3的大小关系是( )A、y1<y3<y2 B、y3<y1<y2 C、y1<y2<y3 D、y2<y3<y1二、填空题
-
13. |+12|=;|0|=;|﹣2.1|= .14. 某人把50粒黄豆染色后与一袋黄豆充分混匀,接着抓出100粒黄豆,数出其中有10粒黄豆被染色,则这袋黄豆原来约有粒.
15. 已知方程组 有正整数解,则整数m的值为 .16. 如图,在菱形纸片ABCD中,AB=3,∠A=60°,将菱形纸片翻折,使点A落在CD的中点E处,折痕为FG,点F,G分别在边AB,AD上,则tan∠EFG的值为 . 17. 函数 的图象不经过第象限.18. 在平面直角坐标系中,点A坐标为(1,0),线段OA绕原点O沿逆时针方向旋转45°,并且每次的长度增加一倍,例如:OA1=2OA,∠A1OA=45°.按照这种规律变换下去,点A2017的纵坐标为 .
17. 函数 的图象不经过第象限.18. 在平面直角坐标系中,点A坐标为(1,0),线段OA绕原点O沿逆时针方向旋转45°,并且每次的长度增加一倍,例如:OA1=2OA,∠A1OA=45°.按照这种规律变换下去,点A2017的纵坐标为 .
三、解答题
-
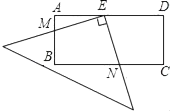
19. 计算:2cos30°﹣2sin45°+3tan60°+|1﹣ |.20. 已知:ax=by=cz=1,求 的值.21. 在矩形ABCD中,AD=2AB,E是AD的中点,一块三角板的直角顶点与点E重合,两直角边与AB,BC分别交于点M,N,求证:BM=CN.
 22. 为弘扬中华优秀传统文化,今年2月20日举行了襄阳市首届中小学生经典诵读大赛决赛. 某中学为了选拔优秀学生参加,广泛开展校级“经典诵读”比赛活动,比赛成绩评定为A,B,C,D,E五个等级,该校七(1)班全体学生参加了学校的比赛,并将比赛结果绘制成如下两幅不完整的统计图.请根据图中信息,解答下列问题:
22. 为弘扬中华优秀传统文化,今年2月20日举行了襄阳市首届中小学生经典诵读大赛决赛. 某中学为了选拔优秀学生参加,广泛开展校级“经典诵读”比赛活动,比赛成绩评定为A,B,C,D,E五个等级,该校七(1)班全体学生参加了学校的比赛,并将比赛结果绘制成如下两幅不完整的统计图.请根据图中信息,解答下列问题: (1)、该校七(1)班共有名学生;扇形统计图中C等级所对应扇形的圆心角等于度;(2)、补全条形统计图;(3)、若A等级的4名学生中有2名男生2名女生,现从中任意选取2名参加学校培训班,请用列表法或画树状图的方法,求出恰好选到1名男生和1名女生的概率.23. 手机下载一个APP,缴纳一定数额的押金,就能以每小时0.5到1元的价格解锁一辆自行车任意骑行…最近的网红非“共享单车”莫属.共享单车为解决市民出行的“最后一公里”难题帮了大忙,人们在享受科技进步、共享经济带来的便利的同时,随意停放、加装私锁、大卸八块等毁坏单车的行为也层出不穷.某共享单车公司一月投入部分自行车进入市场,一月底发现损坏率不低于10%,二月初又投入1200辆进入市场,使可使用的自行车达到7500辆.
(1)、该校七(1)班共有名学生;扇形统计图中C等级所对应扇形的圆心角等于度;(2)、补全条形统计图;(3)、若A等级的4名学生中有2名男生2名女生,现从中任意选取2名参加学校培训班,请用列表法或画树状图的方法,求出恰好选到1名男生和1名女生的概率.23. 手机下载一个APP,缴纳一定数额的押金,就能以每小时0.5到1元的价格解锁一辆自行车任意骑行…最近的网红非“共享单车”莫属.共享单车为解决市民出行的“最后一公里”难题帮了大忙,人们在享受科技进步、共享经济带来的便利的同时,随意停放、加装私锁、大卸八块等毁坏单车的行为也层出不穷.某共享单车公司一月投入部分自行车进入市场,一月底发现损坏率不低于10%,二月初又投入1200辆进入市场,使可使用的自行车达到7500辆.
(1)、一月份该公司投入市场的自行车至少有多少辆?
(2)、二月份的损坏率达到20%,进入三月份,该公司新投入市场的自行车比二月份增长4a%,由于媒体的关注,毁坏共享单车的行为引起了一场国民素质的大讨论,三月份的损坏率下降 a%,三月底可使用的自行车达到7752辆,求a的值.
24. 如图,在△ABC中,AB=AC,以AB为直径作圆O,分别交BC于点D,交CA的延长线于点E,过点D作DH⊥AC于点H,连接DE交线段OA于点F.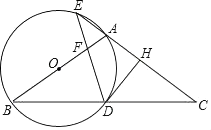 (1)、求证:DH是圆O的切线;(2)、若A为EH的中点,求 的值;
(1)、求证:DH是圆O的切线;(2)、若A为EH的中点,求 的值;
(3)、若EA=EF=1,求圆O的半径.25. 如图,在平面直角坐标系xOy中,A、B为x轴上两点,C、D为y轴上的两点,经过点A、C、B的抛物线的一部分c1与经过点A、D、B的抛物线的一部分c2组合成一条封闭曲线,我们把这条封闭曲线成为“蛋线”.已知点C的坐标为(0,﹣ ),点M是抛物线C2:y=mx2﹣2mx﹣3m(m<0)的顶点.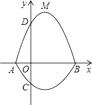 (1)、求A、B两点的坐标;
(1)、求A、B两点的坐标;
(2)、“蛋线”在第四象限上是否存在一点P,使得△PBC的面积最大?若存在,求出△PBC面积的最大值;若不存在,请说明理由;
(3)、当△BDM为直角三角形时,求m的值.