广西柳州市十二中2018届九年级数学中考模拟试卷
试卷更新日期:2018-07-23 类型:中考模拟
一、单选题
-
1. 人类的遗传物质是DNA,人类的DNA是很大的链,最短的22号染色体也长达30000000个核苷酸,30000000用科学记数法表示为( )A、3×108 B、3×107 C、3×106 D、0.3×1082. 如图所示,左面水杯的俯视图是( )
 A、
A、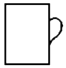 B、
B、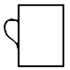 C、
C、 D、
D、 3. 计算 的结果是( )A、 B、 C、 D、4. 一个盒子中装有四张完全相同的卡片,分别写着2cm,3cm,4cm和5cm,盒子外有两张卡片,分别写着3cm和5cm,现随机从盒中取出一张卡片,与盒子外的两张卡片放在一起,以卡片上的数量分别作为三条线段的长度,那么这三条线段能构成三角形的概率是( )A、 B、 C、 D、5. 如图,一束光线与水平面成 的角度照射地面,现在地面AB上支放一个平面镜CD,使这束光线经过平面镜反射后成水平光线,则平面镜CD与地面AB所成角∠DCB的度数等于( )
3. 计算 的结果是( )A、 B、 C、 D、4. 一个盒子中装有四张完全相同的卡片,分别写着2cm,3cm,4cm和5cm,盒子外有两张卡片,分别写着3cm和5cm,现随机从盒中取出一张卡片,与盒子外的两张卡片放在一起,以卡片上的数量分别作为三条线段的长度,那么这三条线段能构成三角形的概率是( )A、 B、 C、 D、5. 如图,一束光线与水平面成 的角度照射地面,现在地面AB上支放一个平面镜CD,使这束光线经过平面镜反射后成水平光线,则平面镜CD与地面AB所成角∠DCB的度数等于( )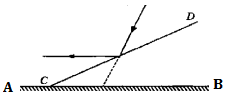 A、 B、45° C、50° D、60°6. 下列运算正确的是( )A、a-2a=a B、(-2a2)3=﹣8a6 C、a6+a3=a2 D、(a+b)2=a2+b27. 如图,已知棋子“卒”的坐标为(-2,3),棋子“马”的坐标为(1,3),则棋子“炮”的坐标为( )
A、 B、45° C、50° D、60°6. 下列运算正确的是( )A、a-2a=a B、(-2a2)3=﹣8a6 C、a6+a3=a2 D、(a+b)2=a2+b27. 如图,已知棋子“卒”的坐标为(-2,3),棋子“马”的坐标为(1,3),则棋子“炮”的坐标为( )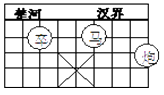 A、(4,2) B、(4,1) C、(2,2) D、(-2,2)8. 在△ABC中,∠A-∠B = 90°,则△ABC为( )三角形.
A、(4,2) B、(4,1) C、(2,2) D、(-2,2)8. 在△ABC中,∠A-∠B = 90°,则△ABC为( )三角形.
A、锐角三角形 B、直角三角形 C、钝角三角形 D、无法确定9. 老师要求同学们课后自作既是轴对称又是中心对称的图形,结果有以下几个,其中符合条件的有( ) 。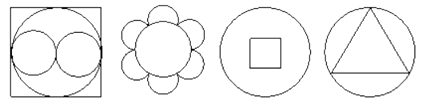 A、1个 B、2个 C、3个 D、4个10. 如图,已知△ABC为等边三角形,AB=2,点D为边AB上一点,过点D作DE∥AC,交BC于E点;过E点作EF⊥DE,交AB的延长线于F点.设AD=x,△DEF的面积为y,则能大致反映y与x函数关系的图象是( )
A、1个 B、2个 C、3个 D、4个10. 如图,已知△ABC为等边三角形,AB=2,点D为边AB上一点,过点D作DE∥AC,交BC于E点;过E点作EF⊥DE,交AB的延长线于F点.设AD=x,△DEF的面积为y,则能大致反映y与x函数关系的图象是( )
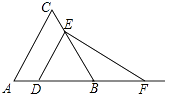
A、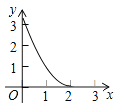 B、
B、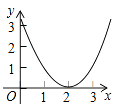 C、
C、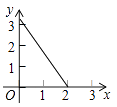 D、
D、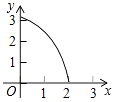
二、填空题
-
11. 某不等式的解集在数轴上的表示如下图所示,则该不等式的解集是 .
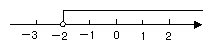 12. 如图,已知∠1=∠2,AC=AD,请增加一个条件,使△ABC≌△AED,你添加的条件是 .
12. 如图,已知∠1=∠2,AC=AD,请增加一个条件,使△ABC≌△AED,你添加的条件是 .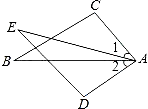 13. 一次函数y=mx+n的图象经过一、三、四象限,则化简 所得的结果 .14. 已知x=﹣1是一元二次方程ax2+bx﹣2=0的一个根,那么b﹣a的值等于.15. 如图,四边形ABCD是正方形,延长AB到E,使AE=AC,则∠BCE的度数是度.
13. 一次函数y=mx+n的图象经过一、三、四象限,则化简 所得的结果 .14. 已知x=﹣1是一元二次方程ax2+bx﹣2=0的一个根,那么b﹣a的值等于.15. 如图,四边形ABCD是正方形,延长AB到E,使AE=AC,则∠BCE的度数是度.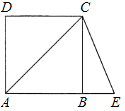 16. 在矩形ABCD中,∠B的角平分线BE与AD交于点E,∠BED的角平分线EF与DC交于点F,若AB=9,DF=2FC,则BC= . (结果保留根号)
16. 在矩形ABCD中,∠B的角平分线BE与AD交于点E,∠BED的角平分线EF与DC交于点F,若AB=9,DF=2FC,则BC= . (结果保留根号)
三、解答题
-
17. 解方程:3x-7(x-1)=3-2(x+3)18. 学校分配学生住宿,如果每室住8人,还少12个床位,如果每室住9人,则空出两个房间。求房间的个数和学生的人数。19. “ 六一”儿童节前夕,某县教育局准备给留守儿童赠送一批学习用品,先对某小学的留守儿童人数进行抽样统计,发现各班留守儿童人数分别为6名,7 名,8 名,10 名,12 名这五种情形,并将统计结果绘制成了如图所示的两幅不完整的统计图.
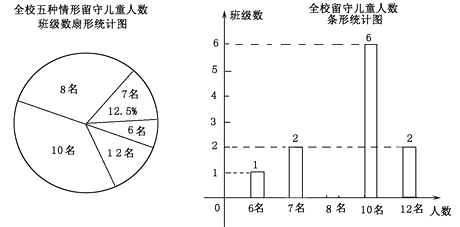
请根据上述统计图,解答下列问题:
(1)、该校有个班级;各班留守儿童人数的中位数是;并补全条形统计图;(2)、若该镇所有小学共有65 个教学班,请根据样本数据,估计该镇小学生中,共有多少名留守儿童.
20. 如图,游客在点A处坐缆车出发,沿A﹣B﹣D的路线可至山顶D处,假设AB和BD都是直线段,且AB=BD=600m,α=75°,β=45°,求DE的长.(参考数据:sin75°≈0.97,cos75°≈0.26, ≈1.41)
 21. 我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18 ℃的条件下生长最快的新品种.如图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线y= 的一部分.请根据图中信息解答下列问题:
21. 我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18 ℃的条件下生长最快的新品种.如图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线y= 的一部分.请根据图中信息解答下列问题: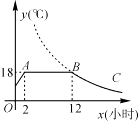 (1)、恒温系统在这天保持大棚内温度18 ℃的时间有多少小时?
(1)、恒温系统在这天保持大棚内温度18 ℃的时间有多少小时?
(2)、求k的值;
(3)、当x=16时,大棚内的温度约为多少度?