广西贵港市平南县2018届九年级中考数学二模试卷

试卷更新日期：2018-07-23 类型：中考模拟

进入出卷网下载

一、单选题

1. ﹣3的绝对值是（）

A、3 B、﹣3 C、0 D、1

查看试题解析
2. 2017年5月，“一带一路”论坛峰会在北京隆重召开，促进了我国与世界各国的互联互通互惠，“一带一路”地区覆盖总人数约为44亿人，44亿这个数用科学记数法表示（）

A、 $4.4 \times 10^{8}$ B、 $4.4 \times 10^{9}$ C、 $44 \times 10^{9}$ D、 $44 \times 10^{8}$

查看试题解析
3. 将如图所示的Rt△ABC绕直角边AC旋转一周，所得几何体的主视图是（）

A、 B、 C、 D、

查看试题解析
4. 若点M在第一、三象限的角平分线上，且点M到x轴的距离为2，则点M的坐标是（）

A、（2，2） B、（-2，-2） C、（2，2）或（-2，-2） D、（2，-2）或（-2，2）

查看试题解析
5. 下列四个命题中，真命题的是（）

A、相等的圆心角所对的弧相等 B、同旁内角互补 C、平行四边形是轴对称图形 D、全等三角形对应边上的高相等

查看试题解析
6. 关于 $x$ 的方程 $x^{2} + 5 x + m = 0$ 的一个根为 $- 2$ ，则 $m$ 的值为（）

A、 $6$ B、 $3$ C、 $- 3$ D、 $- 6$

查看试题解析
7. 如图，⊙O中，弦AB，CD相交于点P，∠A=42°，∠APD=77°，则∠B的大小是（）

A、34° B、35° C、43° D、44°

查看试题解析
8. 给出下列函数：① $y = {\begin{matrix} 3 x - 1 ， (x \geq 1) \\ - 3 x - 1 ， (x < 1) \end{matrix}$ ； ② $y = \frac{3}{x}$ ； ③ $y = - 3 x^{2}$ ．从中任取一个函数，取出的函数符合条件“当 $x > 1$ 时，函数值 $y$ 随 $x$ 增大而减小”的概率是（）．

A、 $1$ B、 $\frac{2}{3}$ C、 $\frac{1}{3}$ D、 $0$

查看试题解析
9. 如图，在直角坐标系中，点A在函数y＝ $\frac{4}{x}$ (x＞0)的图象上，AB⊥x轴于点B，AB的垂直平分线与y轴交于点C，与函数y＝ $\frac{4}{x}$ (x＞0)的图象交于点D，连接AC，CB，BD，DA，则四边形ACBD的面积等于（）

A、2 B、2 $\sqrt{3}$ C、4 D、4 $\sqrt{3}$

查看试题解析
10. 如图，将函数y= $\frac{1}{2}$ （x﹣2）²+1的图象沿y轴向上平移得到一条新函数的图象，其中点A（1，m），B（4，n）平移后的对应点分别为点A'、B'．若曲线段AB扫过的面积为9（图中的阴影部分），则新图象的函数表达式是（）

A、 $y = \frac{1}{2} {(x - 2)}^{2} - 2$ B、 $y = \frac{1}{2} {(x - 2)}^{2} + 7$ C、 $y = \frac{1}{2} {(x - 2)}^{2} - 5$ D、 $y = \frac{1}{2} {(x - 2)}^{2} + 4$

查看试题解析
11. 在正方形ABCD中，点E为BC边的中点，点B′与点B关于AE对称，B′B与AE交于点F，连接AB′，DB′，FC．下列结论：①AB′=AD；②△FCB′为等腰直角三角形；③∠ADB′=75°；④∠CB′D=135°．其中正确的是（）

A、①② B、①②④ C、③④ D、①②③④

查看试题解析

二、填空题

12. 如果分式 $\frac{x}{x - 3}$ 有意义，则 $x$ 的取值范围是．

查看试题解析
13. 分解因式： $a^{3} - a$ = ．

查看试题解析
14. 有一组数据：2、1、 3、5、 $a$ 、6，它的平均数是3，则这组数据的中位数是.

查看试题解析
15. 如图，已知 $a / / b$ ，李明把三角板的直角顶点放在直线 $b$ 上．若∠1=42°，则∠2的度数为.

查看试题解析
16. 如图，AB为半圆O的直径，以AO为直径作半圆M，C为OB的中点，D在半圆M上，且CD⊥MD，延长AD交半圆O于点E，且AB=4，则圆中阴影部分的面积为.

查看试题解析
17. 如图，在直角坐标系中点 $A_{1}$ 的坐标为（1，0），过点 $A_{1}$ 作x轴的垂线交直线y=2x于 $A_{2}$ ，过点 $A_{2}$ 作直线y=2x的垂线交x轴于 $A_{3}$ ，过点 $A_{3}$ 作x轴的垂线交直线y=2x于 $A_{4}$ …，依此规律，则 $A_{2018}$ 的坐标为.

查看试题解析

三、解答题

18.

(1)、计算： ${(- \frac{1}{2})}^{- 1} + \sqrt{12} - {(π - 2018)}^{0} - 4 cos 30^{0}$

(2)、解不等式组： ${\begin{matrix} 3 x \geq 4 (x - 1) \\ 2 - x \leq \frac{x - 2}{3} \end{matrix}$ 并把它的解集在数轴上表示出来.

查看试题解析
19. A，B两所学校在一条东西走向公路的同旁，以公路所在直线为x轴建立如图所示的平面直角坐标系，且点A的坐标是(2，2)，点B的坐标是(7， 3)，根据下列要求作图（保留作图痕迹，不用写作法）.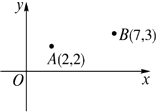

(1)、一辆汽车由西向东行驶，在行驶过程中是否存在一点C，使C点到A，B两校的距离相等？如果有，请用尺规作图找出该点；

(2)、若在公路边建一游乐场P，使游乐场到两校距离之和最小，通过作图在图中找出建游乐场P的位置，P点的坐标为.

查看试题解析
20. 如图，已知反比例函数 $y = \frac{k}{x}$ 的图象经过第二象限内的点A（ $m$ ，4），AB⊥x轴于点B，△AOB的面积为2，若直线 $y = a x + b$ 经过点A，并且经过反比例函数 $y = \frac{k}{x}$ 的图象上另一点C（2， $n$ ）．

(1)、求反比例函数和直线的解析式；

(2)、设直线 $y = a x + b$ 与 $x$ 轴交于点M，求AM的长．

查看试题解析
21. 某校随机抽取部分学生，就“学习习惯”进行调查，将“对自己做错的题目进行整理、分析、改正” (选项为：很少、有时、常常、总是)的调查数据进行了整理，绘制成部分统计图如下：

请根据图中信息，解答下列问题：

(1)、该调查的样本容量为， a=%，b= %， “很少”对应扇形的圆心角为；

(2)、请补全条形统计图；

(3)、若该校共有3500名学生，请你估计其中“总是”对错题进行整理、分析、改正的学生有多少名?

查看试题解析
22. 某水果商场经销一种高档水果，原价每千克50元.

(1)、连续两次降价后每千克32元，若每次下降的百分率相同，求每次下降的百分率；

(2)、这种水果进价为每千克40元，若在销售等各个过程中每千克损耗或开支2.5元，经一次降价销售后商场不亏本，求一次下降的百分率的最大值．

查看试题解析
23. 如图，在矩形 $A B C D$ 中，点 $O$ 在对角线 $A C$ 上，以 $O A$ 的长为半径的圆 $O$ 与 $A D ， A C$ 分别交于点 $E ， F$ ，且 $∠ A C B = ∠ D C E$ ．

(1)、求证： $C E$ 是圆 $O$ 所在圆的切线；

(2)、若 $tan ∠ B A C = \sqrt{2}$ ， $B C = 2$ ，求⊙O的半径．

查看试题解析
24. 如图，已知抛物线 $y = - \frac{1}{4} x^{2} + b x + c$ 与x轴相交于A、B两点，与y轴相交于点C（0，4），若已知A点的坐标为A（﹣2，0）．

(1)、求抛物线的解析式；

(2)、求△ABC的外接圆圆心坐标；

(3)、在抛物线的对称轴上是否存在点Q，使△ACQ为等腰三角形？若存在，求出符合条件的Q点坐标，若不存在，请说明理由．

查看试题解析
25. 如图，在正方形ABCD中，E，G分别在边DA，DC上（不与端点重合），且DE=DG，过D点作DF⊥CE，垂足为F．

(1)、①∠BCE与∠CDF的大小关系是；
②证明：GF⊥BF；

(2)、探究G落在边DC的什么位置时，BF=BC，请说明理由.

查看试题解析