广东省中山市教育联合体2018届数学中考一模试卷

试卷更新日期：2018-07-23 类型：中考模拟

进入出卷网下载

一、单选题

1. ﹣5的相反数是（）

A、﹣5 B、5 C、﹣ $\frac{1}{5}$ D、 $\frac{1}{5}$

查看试题解析
2. 据2017年1月24日《中山日报》报道，三乡镇2016年财政收入突破180亿元，在中山各乡镇中排名第二．将180亿用科学记数法表示为（）

A、1.8×10 B、1.8×10⁸ C、1.8×10⁹ D、1.8×10¹⁰

查看试题解析
3. 下列运算正确的是（）

A、 $\sqrt{9} = \pm 3$ B、（m²）³=m⁵ C、a²•a³=a⁵ D、（x+y）²=x²+y²

查看试题解析
4. 已知正n边形的一个内角为135°，则边数n的值是（）

A、6 B、7 C、8 D、10

查看试题解析
5. 下图中是中心对称图形而不是轴对称图形的共有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
6. 在中山市举行“慈善万人行”大型募捐活动中，某班50位同学捐款金额统计如下：
金额（元）
20
30
35
50
100
学生数（人）
20
10
5
10
5
则在这次活动中，该班同学捐款金额的众数和中位数分别是（）

A、20元，30元 B、20元，35元 C、100元，35元 D、100元，30元．

查看试题解析
7. 小明想用一个圆心角为120°，半径为6cm的扇形做一个圆锥的侧面（接缝处忽略不计），则做成的圆锥底面半径为（）

A、1 cm B、2 cm C、3 cm D、4cm

查看试题解析
8. 如图，P是反比例函数图象上第二象限内一点，若矩形PEOF的面积为3，则反比例函数的解析式是（）

A、y= $- \frac{3}{x}$ B、y=﹣ $\frac{x}{3}$ C、y= $\frac{x}{3}$ D、y= $\frac{3}{x}$

查看试题解析
9. 如图，已知⊙O为四边形ABCD的外接圆，O为圆心，若∠BCD=120°，AB=AD=2，则⊙O的半径长为（）

A、 $\frac{3 \sqrt{2}}{2}$ B、 $\frac{\sqrt{6}}{2}$ C、 $\frac{3}{2}$ D、 $\frac{2 \sqrt{3}}{3}$

查看试题解析
10. 如图．在Rt△AOB中，∠AOB=90°，OA=3，OB=2，将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE，将线段EF绕点E逆时针旋转90°后得线段ED，分别以O，E为圆心，OA、ED长为半径画弧AF和弧DF，连接AD，则图中阴影部分面积是（）

A、8﹣π B、 $\frac{5 π}{4}$ C、3+π D、π

查看试题解析

二、填空题

11. 分解因式：xy²﹣4x= ．

查看试题解析
12. 已知式子 $\frac{\sqrt{1 - x}}{x + 3}$ 有意义，则x的取值范围是

查看试题解析
13. 不等式组 ${\begin{matrix} x - 1 < 0 \\ x + 2 \geq 0 \end{matrix}$ 的解集是．

查看试题解析
14. 如图是二次函数 $y_{1} = a x^{2} + b x + c$ 和一次函数y₂=kx+t的图象，当y₁≥y₂时，x的取值范围是．

查看试题解析
15. 若x=3﹣ $\sqrt{2}$ ，则代数式x²﹣6x+9的值为．

查看试题解析

三、解答题

16. 计算：|﹣2|+2^﹣¹﹣cos60°﹣（1﹣ $\sqrt{2}$ ）⁰ ．

查看试题解析
17. 先化简，再求值：先化简 $\frac{x^{2} - 2 x + 1}{x^{2} - 1}$ ÷（ $\frac{x - 1}{x + 1}$ ﹣x+1），然后从﹣2＜x＜ $\sqrt{5}$ 的范围内选取一个合适的整数作为x的值代入求值．

查看试题解析
18. 某种植物的主干长出若干数目的支干，每个支干又长出同样数目的小分支，主干、支干和小分支的总数是91，每个支干长出多少小分支？

查看试题解析
19. 如图，△ABC中，∠ACB＞∠ABC．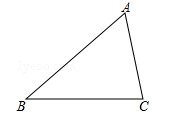

(1)、用直尺和圆规在∠ACB的内部作射线CM，使∠ACM=∠ABC（不要求写作法，保留作图痕迹）；

(2)、若（1）中的射线CM交AB于点D，AB=9，AC=6，求AD的长．

查看试题解析
20. 纪中三鑫双语学校准备开展“阳光体育活动”，决定开设足球、篮球、乒乓球、羽毛球、排球等球类活动，为了了解学生对这五项活动的喜爱情况，随机调查了m名学生（每名学生必选且只能选择这五项活动中的一种）．
根据以上统计图提供的信息，请解答下列问题：

(1)、m= ， n= ．

(2)、补全上图中的条形统计图．

(3)、在抽查的m名学生中，有小薇、小燕、小红、小梅等10名学生喜欢羽毛球活动，学校打算从小薇、小燕、小红、小梅这4名女生中，选取2名参加全市中学生女子羽毛球比赛，请用列表法或画树状图法，求同时选中小红、小燕的概率．（解答过程中，可将小薇、小燕、小红、小梅分别用字母A、B、C、D代表）

查看试题解析
21. 如图，BD是△ABC的角平分线，点E，F分别在BC，AB上，且DE∥AB，BE=AF．

(1)、求证：四边形ADEF是平行四边形；

(2)、若∠ABC=60°，BD=4，求平行四边形ADEF的面积．

查看试题解析
22. 如图，抛物线y=﹣ $\frac{4}{3} x^{2}$ +bx+c过点A（3，0），B（0，2）．M（m，0）为线段OA上一个动点（点M与点A不重合），过点M作垂直于x轴的直线与直线AB和抛物线分别交于点P、N．

(1)、求直线AB的解析式和抛物线的解析式；

(2)、如果点P是MN的中点，那么求此时点N的坐标；

(3)、在对称轴的左侧是否存在点M使四边形OMPB的面积最大，如果存在求点M的坐标；不存在请说明理由．

查看试题解析
23. 如图1，⊙O的直径AB=12，P是弦BC上一动点（与点B，C不重合），∠ABC=30°，过点P作PD⊥OP交⊙O于点D．

(1)、如图2，当PD∥AB时，求PD的长；

(2)、如图3，当弧DC=弧AC时，延长AB至点E，使BE= $\frac{1}{2}$ AB，连接DE．
①求证：DE是⊙O的切线；

查看试题解析
24. 在正方形ABCD中，AB=8，点P在边CD上，tan∠PBC= $\frac{3}{4}$ ，点Q是在射线BP上的一个动点，过点Q作AB的平行线交射线AD于点M，点R在射线AD上，使RQ始终与直线BP垂直．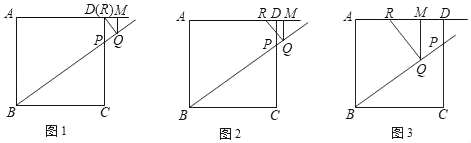

(1)、如图1，当点R与点D重合时，求PQ的长；

(2)、如图2，试探索： $\frac{R M}{M Q}$ 的比值是否随点Q的运动而发生变化？若有变化，请说明你的理由；若没有变化，请求出它的比值；

(3)、如图3，若点Q在线段BP上，设PQ=x，RM=y，求y关于x的函数关系式，并写出它的定义域．

查看试题解析

金额（元）	20	30	35	50	100
学生数（人）	20	10	5	10	5