广东省阳江市江城区2018届数学中考一模试卷

试卷更新日期：2018-07-23 类型：中考模拟

进入出卷网下载

一、单选题

1. 计算3×（﹣2）的结果是（）

A、5 B、﹣5 C、6 D、﹣6

查看试题解析
2. 小张抛一枚质地均匀的硬币，出现正面朝上的可能性是（）

A、25% B、50% C、75% D、85%

查看试题解析
3. 已知等腰三角形的两条边长分别是7和3，则下列四个数中，第三条边的长是（）

A、8 B、7 C、4 D、3

查看试题解析
4. 一个正比例函数的图象过点（2，﹣3），它的表达式为（）

A、 $y = - \frac{3}{2} x$ B、 $y = \frac{2}{3} x$ C、 $y = \frac{3}{2} x$ D、 $y = - \frac{2}{3} x$

查看试题解析
5. 如图，是由五个相同的小正方体组成的几何体，则它的左视图是（）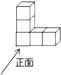

A、 B、 C、 D、

查看试题解析
6. 如图，△ABC内有一点D，且DA=DB=DC，若∠DAB=20°，∠DAC=30°，则∠BDC的大小是（）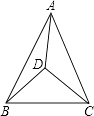

A、100° B、80° C、70° D、50°

查看试题解析
7. 如图，在⊙O中，OA=AB，OC⊥AB，则下列结论错误的是（）

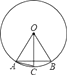A、弦AB的长等于圆内接正六边形的边长 B、弦AC的长等于圆内接正十二边形的边长 C、 $\overset{⌢}{A C} = \overset{⌢}{B C}$ D、∠BAC=30°

查看试题解析
8. 不等式 ${\begin{matrix} \frac{1}{3} x + 1 > 0 \\ 2 - x \geq 0 \end{matrix}$ 的解集是（）

A、﹣ $\frac{1}{3}$ ＜x≤2 B、﹣3＜x≤2 C、x≥2 D、x＜﹣3

查看试题解析
9. 如图，▱ABCD的周长是28cm，△ABC的周长是22cm，则AC的长为（）

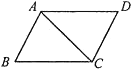A、6cm B、12cm C、4cm D、8cm

查看试题解析
10. 已知二次函数y=ax²+bx+c（a≠0）的图象如图，且关于x的一元二次方程ax²+bx+c﹣m=0没有实数根，有下列结论：①b²﹣4ac＞0；②abc＜0；③m＞2．其中，正确结论的个数是（）.

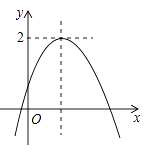A、0 B、1 C、2 D、3

查看试题解析

二、填空题

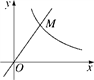
11. 分解因式：ax⁴﹣9ay²= ．

查看试题解析
12. 如图，点M是函数y＝ $\sqrt{3}$ x与y＝ $\frac{k}{x}$ 的图象在第一象限内的交点，OM＝4，则k的值为．

查看试题解析
13. 如图，在△ABC中，AB≠AC．D、E分别为边AB、AC上的点．AC=3AD，AB=3AE，点F为BC边上一点，添加一个条件：，可以使得△FDB与△ADE相似．（只需写出一个）

查看试题解析
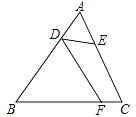14. 如图，点A（3，t）在第一象限，OA与x轴所夹的锐角为α，tanα= $\frac{3}{2}$ ，则t的值是．

查看试题解析
15. 若y＝ $\sqrt{x - 3}$ ＋ $\sqrt{3 - x}$ ＋2，则x^y＝．

查看试题解析
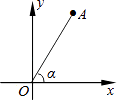16. 如图，在Rt△ABC中，∠ACB＝90°，AC＝4，BC＝2.分别以AC，BC为直径画半圆，则图中阴影部分的面积为． (结果保留π)

查看试题解析

三、解答题

17. 计算：（﹣1）⁰+|2﹣ $\sqrt{3}$ |+3tan30°

查看试题解析
18. 先化简，再求值：（ $\frac{3 x}{x - 1} - \frac{x}{x + 1}$ ） $\cdot \frac{x^{2} - 1}{2 x}$ ，其中x=﹣3．

查看试题解析
19. 在Rt△ABC中，∠C=90°．

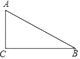(1)、求作：∠A的平分线AD，AD交BC于点D；（保留作图痕迹，不写作法）

(2)、若点D恰好在线段AB的垂直平分线上，求∠A的度数．

查看试题解析
20. 某电冰箱厂每个月的产量都比上个月增长的百分数相同．已知该厂今年4月份的电冰箱产量为5万台，6月份比5月份多生产了1.2万台．

(1)、求该厂今年产量的月平均增长率为多少？

(2)、预计7月份的产量为多少万台？

查看试题解析
21. 国家规定“中小学生每天在校体育活动时间不低于1小时”．为此，我区就“你每天在校体育活动时间是多少”的问题随机调查了区内300名初中学生．根据调查结果绘制成的统计图（部分）如图所示，其中分组情况是：
A组：t＜0.5h B组：0.5h≤t＜1h C组：1h≤t＜1.5h D组：t≥1.5h
请根据上述信息解答下列问题：

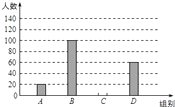(1)、C组的人数是．

(2)、本次调查数据的中位数落在组内；

(3)、若我区有5400名初中学生，请你估计其中达国家规定体育活动时间的人约有多少？

查看试题解析
22. 如图，小丽准备测一根旗杆AB的高度，已知小丽的眼睛离地面的距离EC=1.5米，第一次测量点C和第二次测量点D之间的距离CD=10米，∠AEG=30°，∠AFG=60°，请你帮小丽计算出这根旗杆的高度．（结果保留根号）

查看试题解析
23. 如图，A（4，0），B（1，3），以OA、OB为边作平行四边形OACB，反比例函数y= $\frac{k}{x}$ 的图象经过点C．

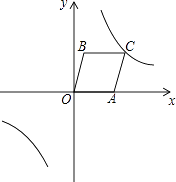(1)、求k的值；

(2)、根据图象，直接写出y＜3时自变量x的取值范围；

(3)、将平行四边形OACB向上平移几个单位长度，使点B落在反比例函数的图象上．

查看试题解析
24. 如图， $A B$ 是⊙ $O$ 的直径，点 $C$ 是⊙ $O$ 上一点， $A D$ 与过点 $C$ 的切线垂直，垂足为点 $D$ ，直线 $D C$ 与 $A B$ 的延长线相交于点 $P$ ，弦 $C E$ 平分∠ $A C B$ ，交 $A B$ 于点 $F$ ，连接 $B E$ ．

(1)、求证： $A C$ 平分∠ $D A B$ ；

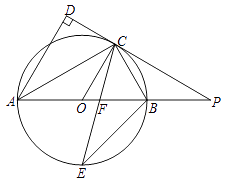(2)、求证：PC=PF；

(3)、若 $tan ∠ A B C = \frac{4}{3}$ ，AB=14，求线段 $P C$ 的长．

查看试题解析
25. 已知：把Rt△ABC和Rt△DEF按如图（1）摆放（点C与点E重合），点B、C（E）、F在同一条直线上，∠ACB=∠EDF=90°，∠DEF=45°，AC=8cm，BC=6cm，EF=9cm．如图（2），△DEF从图（1）的位置出发，以1cm/s的速度沿CB向△ABC匀速移动，在△DEF移动的同时，点P从△ABC的顶点B出发，以2cm/s的速度沿BA匀速移动，当△DEF的顶点D移动到AC边上时，△DEF停止移动，点P也随之停止移动，DE与AC相交于点Q，连接PQ，设移动时间为t（s）（0＜t＜4.5）．
解答下列问题：

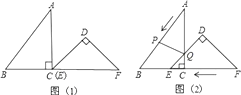(1)、当t为何值时，点A在线段PQ的垂直平分线上？

(2)、连接PE，设四边形APEC的面积为y（cm²），求y与t之间的函数关系式，是否存在某一时刻t，使面积y最小？若存在，求出y的最小值；若不存在，说明理由；

(3)、是否存在某一时刻t，使P、Q、F三点在同一条直线上？若存在，求出此时t的值；若不存在，说明理由．

查看试题解析