广东省汕头市2018届九年级数学中考模拟试卷

试卷更新日期：2018-07-23 类型：中考模拟

进入出卷网下载

一、单选题

1. ﹣2018的绝对值是（）

A、±2018 B、﹣2018 C、﹣ $\frac{1}{2018}$ D、2018

查看试题解析
2. 一种病毒长度约为0.000056mm，用科学记数法表示这个数为（）mm.

A、5.6×10^﹣⁶ B、5.6×10^﹣⁵ C、0.56×10^﹣⁵ D、56×10^﹣⁶

查看试题解析
3. 下列计算正确的是（　　）

A、（﹣a³）²=﹣a⁶ B、（a﹣b）²=a²﹣b² C、3a²+2a³=5a⁵ D、a⁶÷a³=a³

查看试题解析
4. 一元二次方程x²+2x﹣4=0的根的情况为（　　）

A、没有实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、无法确定

查看试题解析
5. 在△ABC中，∠C=90°，如果AB=6，BC=3，那么cosB的值是（）

A、 $\frac{\sqrt{3}}{2}$ B、 $\frac{\sqrt{5}}{5}$ C、 $\frac{\sqrt{3}}{3}$ D、 $\frac{1}{2}$

查看试题解析
6. 以方程组 ${\begin{matrix} y = - x + 2 \\ y = x - 1 \end{matrix}$ 的解为坐标的点 $(x ， y)$ 在平面直角坐标系中的位置是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
7. 如图所示，为估算某河的宽度，在河对岸的边上选定一个目标点A，在近岸取点B，C，D，使得AB⊥BC，CD⊥BC，点E在BC上，并且点A，E，D在同一条直线上，若测得BE＝20m，EC＝10m，CD＝20m，则河的宽度AB的长为（）

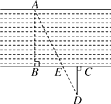A、60m B、40m C、30m D、20m

查看试题解析
8. 如图，一个梯子AB长2.5米，顶端A靠在墙AC上，这时梯子下端B与墙角C距离为1.5米，梯子滑动后停在DE的位置上，测得BD长为0.9米，则梯子顶端A下落了（）

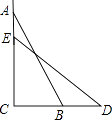A、0.9米 B、1.3米 C、1.5米 D、2米

查看试题解析
9. 某旅游公司2012年三月份共接待游客16万人次，2012年五月份共接待游客81万人次．设每月的平均增长率为x，则可列方程为（）

A、16（1+x）²=81 B、16（1﹣x）²=81 C、81（1+x）²=16 D、81（1﹣x）²=16

查看试题解析

二、填空题

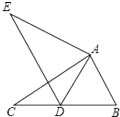
10. 函数y= $\sqrt{3 x - 5}$ 的自变量x的取值范围为．

查看试题解析
11. 因式分解：m³n﹣9mn= ．

查看试题解析
12. 分式方程 $\frac{2}{x} = \frac{3}{x + 1}$ 的解为x= ．

查看试题解析
13. 在一个不透明的盒子中装有8个白球和若干个黄球，它们除颜色不同外，其余均相同．若从中随机摸出1个球，它恰好是白球的概率是 $\frac{2}{3}$ ，则该盒中黄球的个数为．

查看试题解析
14. 若 $\sqrt{a - 3}$ +（b+4）²=0，那么点（a，b）关于原点对称点的坐标是．

查看试题解析
15. 如图，在△ABC中，AB=2，BC=3.5，∠B=60°，将△ABC绕点A按顺时针旋转一定角度得到△ADE，当点B的对应点D恰好落在BC边上时，则CD的长为．

查看试题解析

三、解答题

16. 计算： $\sqrt{8}$ ×sin45°+（ $\frac{1}{2}$ ）^﹣¹﹣（ $\sqrt{2}$ ﹣1）⁰

查看试题解析
17. 解不等式组： ${\begin{matrix} 4 x + 6 > 1 - x ， \\ 3 (x - 1) \leq x + 5 ， \end{matrix}$ 并把解集在数轴上表示出来.

查看试题解析
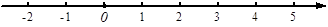18. 已知：如图，在△ABC中，∠A=30°，∠B=60°．

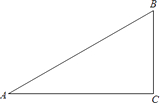(1)、①作∠B的平分线BD，交AC于点D；
②作AB的中点E（要求：尺规作图，保留作图痕迹，不必写作法和证明）；

(2)、连接DE，求证：△ADE≌△BDE．

查看试题解析
19. 某中学九年级（1）班为了了解全班学生的兴趣爱好情况，采取全面调查的方法，从舞蹈、书法、唱歌、绘画等四个方面调查了全班学生的兴趣爱好，根据调查的结果组建了4个兴趣小组，并绘制成如图所示的两幅不完整的统计图（如图①，②，要求每位学生只能选择其中一种自己喜欢的兴趣项目），请你根据图中提供的信息解答下列问题：

(1)、九年级（1）班的学生人数为，并将图①中条形统计图补充完整；

(2)、图②中表示“绘画”的扇形的圆心角是度；

(3)、“舞蹈”兴趣小组4名学生中有3男1女，现在打算从中随机选出2名学生参加学校的舞蹈队，请用列表或画树状图的方法求选出的2名学生恰好是1男1女的概率．

查看试题解析
20. 已知：如图，在平面直角坐标系xOy中，直线AB与x轴交于点A（－2，0），与反比例函数在第一象限内的图象的交于点B（2，n），连结BO，若S_△AOB＝4．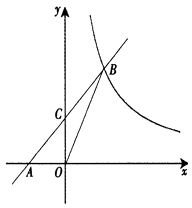

(1)、求该反比例函数的解析式和直线AB的解析式；

(2)、若直线AB与y轴的交点为C，求△OCB的面积．

查看试题解析
21. 如图所示，一条自西向东的观光大道l上有A、B两个景点，A、B相距2km，在A处测得另一景点C位于点A的北偏东60°方向，在B处测得景点C位于景点B的北偏东45°方向，求景点C到观光大道l的距离．（结果精确到0.1km）

查看试题解析
22. 如图，已知正比例函数y=2x与反比例函数y= $\frac{k}{x}$ （k＞0）的图象交于A、B两点，且点A的横坐标为4，

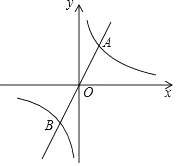(1)、求k的值；

(2)、根据图象直接写出正比例函数值小于反比例函数值时x的取值范围；

(3)、过原点O的另一条直线l交双曲线y= $\frac{k}{x}$ （k＞0）于P、Q两点（P点在第一象限），若由点A、P、B、Q为顶点组成的四边形面积为224，求点P的坐标．

查看试题解析
23. 如图，在△ABC中，AB=BC，以BC为直径的⊙O交AC于点D，过点D作DE⊥AB，DF⊥BC，垂足分别为E、F．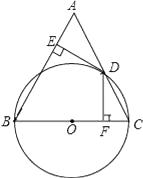

(1)、求证：ED是⊙O的切线；

(2)、若DF=3 $\sqrt{5}$ ，cosA= $\frac{2}{3}$ ，求⊙O的直径．

查看试题解析
24. 如图，抛物线y=﹣x²+2x+3与x轴相交于A、B两点（点A在点B的左侧），与y轴相交于点C，顶点为D．

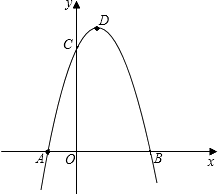(1)、直接写出A、B、C三点的坐标和抛物线的对称轴；

(2)、连接BC，与抛物线的对称轴交于点E，点P为线段BC上的一个动点，过点P作PF∥DE交抛物线于点F，设点P的横坐标为m；
①用含m的代数式表示线段PF的长，并求出当m为何值时，四边形PEDF为平行四边形？
②设△BCF的面积为S，求S与m的函数关系式．

查看试题解析