2016年广东省广州市中考数学试卷

试卷更新日期：2017-02-09 类型：中考真卷

进入出卷网下载

一、选择题．

1. 中国人很早开始使用负数，中国古代数学著作《九章算术》的“方程”一章，在世界数学史上首次正式引入负数．如果收入100元记作+100元．那么﹣80元表示（）

A、支出20元 B、收入20元 C、支出80元 D、收入80元

查看试题解析
2. 如图所示的几何体左视图是（）

A、 B、 C、 D、

查看试题解析
3. 据统计，2015年广州地铁日均客运量均为6 590 000人次，将6 590 000用科学记数法表示为（）

A、6.59×10⁴ B、659×10⁴ C、65.9×10⁵ D、6.59×10⁶

查看试题解析
4. 某个密码锁的密码由三个数字组成，每个数字都是0﹣9这十个数字中的一个，只有当三个数字与所设定的密码及顺序完全相同时，才能将锁打开．如果仅忘记了锁设密码的最后那个数字，那么一次就能打开该密码的概率是（）

A、 $\frac{1}{10}$ B、 $\frac{1}{9}$ C、 $\frac{1}{3}$ D、 $\frac{1}{2}$

查看试题解析
5. 下列计算正确的是（）

A、 $\frac{x^{2}}{y^{2}} = \frac{x}{y} (y \neq 0)$ B、xy²÷ $\frac{1}{2 y} = 2 x y (y \neq 0)$ C、2 $\sqrt{x} + 3 \sqrt{y} = 5 \sqrt{x y} (x \geq 0 ， y \geq 0)$ D、（xy³）²=x²y⁶

查看试题解析
6. 一司机驾驶汽车从甲地去乙地，他以平均80千米/小时的速度用了4个小时到达乙地，当他按原路匀速返回时．汽车的速度v千米/小时与时间t小时的函数关系是（）

A、v=320t B、v= $\frac{320}{t}$ C、v=20t D、v= $\frac{20}{t}$

查看试题解析
7. 如图，已知△ABC中，AB=10，AC=8，BC=6，DE是AC的垂直平分线，DE交AB于点D，连接CD，则CD=（）

A、3 B、4 C、4.8 D、5

查看试题解析
8. 若一次函数y=ax+b的图象经过第一、二、四象限，则下列不等式中总是成立的是（）

A、ab＞0 B、a﹣b＞0 C、a²+b＞0 D、a+b＞0

查看试题解析
9. 对于二次函数y=﹣ $\frac{1}{4} x^{2}$ +x﹣4，下列说法正确的是（）

A、当x＞0时，y随x的增大而增大 B、当x=2时，y有最大值﹣3 C、图象的顶点坐标为（﹣2，﹣7） D、图象与x轴有两个交点

查看试题解析
10. 定义运算：a⋆b=a（1﹣b）．若a，b是方程x²﹣x+ $\frac{1}{4}$ m=0（m＜0）的两根，则b⋆b﹣a⋆a的值为（）

A、0 B、1 C、2 D、与m有关

查看试题解析

二、填空题．（本大题共六小题，每小题3分，满分18分．）

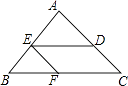
11. 分解因式：2a²+ab= ．

查看试题解析
12. 代数式 $\sqrt{9 - x}$ 有意义时，实数x的取值范围是．

查看试题解析
13. 如图，△ABC中，AB=AC，BC=12cm，点D在AC上，DC=4cm．将线段DC沿着CB的方向平移7cm得到线段EF，点E，F分别落在边AB，BC上，则△EBF的周长为 cm．

查看试题解析
14. 分式方程 $\frac{1}{2 x} = \frac{2}{x - 3}$ 的解是．

查看试题解析
15. 如图，以点O为圆心的两个同心圆中，大圆的弦AB是小圆的切线，点P为切点，AB=12 $\sqrt{3}$ ，OP=6，则劣弧AB的长为．

查看试题解析
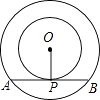16. 如图，正方形ABCD的边长为1，AC，BD是对角线．将△DCB绕着点D顺时针旋转45°得到△DGH，HG交AB于点E，连接DE交AC于点F，连接FG．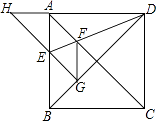
则下列结论：
①四边形AEGF是菱形
②△AED≌△GED
③∠DFG=112.5°
④BC+FG=1.5
其中正确的结论是．

查看试题解析

三、解答题

17. 解不等式组 ${\begin{cases} 2 x < 5 \\ 3 (x + 2) \geq x + 4 \end{cases}$ 并在数轴上表示解集．

查看试题解析
18. 如图，矩形ABCD的对角线AC，BD相交于点O，若AB=AO，求∠ABD的度数．

查看试题解析
19. 某校为了提升初中学生学习数学的兴趣，培养学生的创新精神，举办“玩转数学”比赛．现有甲、乙、丙三个小组进入决赛，评委从研究报告、小组展示、答辩三个方面为各小组打分，各项成绩均按百分制记录．甲、乙、丙三个小组各项得分如表：
小组
研究报告
小组展示
答辩
甲
91
80
78
乙
81
74
85
丙
79
83
90

(1)、计算各小组的平均成绩，并从高分到低分确定小组的排名顺序；

(2)、如果按照研究报告占40%，小组展示占30%，答辩占30%计算各小组的成绩，哪个小组的成绩最高？

查看试题解析
20. 已知A= $\frac{{(a + b)}^{2} - 4 a b}{a b {(a - b)}^{2}}$ （a，b≠0且a≠b）

(1)、化简A；

(2)、若点P（a，b）在反比例函数y=﹣ $\frac{5}{x}$ 的图象上，求A的值．

查看试题解析
21. 如图，利用尺规，在△ABC的边AC上方作∠CAE=∠ACB，在射线AE上截取AD=BC，连接CD，并证明：CD∥AB（尺规作图要求保留作图痕迹，不写作法）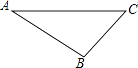

查看试题解析
22. 如图，某无人机于空中A处探测到目标B，D，从无人机A上看目标B，D的俯角分别为30°，60°，此时无人机的飞行高度AC为60m，随后无人机从A处继续飞行30 $\sqrt{3}$ m到达A′处，

(1)、求A，B之间的距离；

(2)、求从无人机A′上看目标D的俯角的正切值．

查看试题解析
23. 如图，在平面直角坐标系xOy中，直线y=﹣x+3与x轴交于点C，与直线AD交于点A（ $\frac{4}{3}$ ， $\fr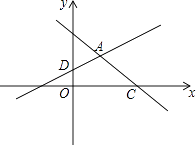ac{5}{3}$ ），点D的坐标为（0，1）

(1)、求直线AD的解析式；

(2)、直线AD与x轴交于点B，若点E是直线AD上一动点（不与点B重合），当△BOD与△BCE相似时，求点E的坐标．

查看试题解析
24. 已知抛物线y=mx²+（1﹣2m）x+1﹣3m与x轴相交于不同的两点A、B

(1)、求m的取值范围；

(2)、证明该抛物线一定经过非坐标轴上的一点P，并求出点P的坐标；

(3)、当 $\frac{1}{4}$ ＜m≤8时，由（2）求出的点P和点A，B构成的△ABP的面积是否有最值？若有，求出该最值及相对应的m值．

查看试题解析
25. 如图，点C为△ABD的外接圆上的一动点（点C不在 $\overset{⌢}{B A D}$ 上，且不与点B，D重合），∠ACB=∠ABD=45°

(1)、求证：BD是该外接圆的直径；

(2)、连结CD，求证： $\sqrt{2}$ AC=BC+CD；

(3)、若△ABC关于直线AB的对称图形为△ABM，连接DM，试探究DM² ， AM² ， BM²三者之间满足的等量关系，并证明你的结论．

查看试题解析

小组	研究报告	小组展示	答辩
甲	91	80	78
乙	81	74	85
丙	79	83	90