福建省漳州市2018届九年级5月质量检测数学试卷

试卷更新日期：2018-07-23 类型：中考模拟

进入出卷网下载

一、单选题

1. 如图，数轴上点M所表示的数的绝对值是（）．

A、3 B、 $- 3$ C、±3 D、 $- \frac{1}{3}$

查看试题解析
2. “中国天眼”FAST射电望远镜的反射面总面积约250 000m² ，数据250 000用科学记数法表示为（）．

A、25×10⁴ B、2.5×10⁵ C、2.5×10⁶ D、0.25×10⁶

查看试题解析
3. 如图是某几何体的左视图，则该几何体不可能是（）．

A、 B、 C、 D、

查看试题解析
4. 下列计算，结果等于x⁵的是（）．

A、 $x^{2} + x^{3}$ B、 $x^{2} \cdot x^{3}$ C、 $x^{10} \div x^{2}$ D、(x²)³

查看试题解析
5. 如图，在下框解分式方程的4个步骤中，根据等式基本性质的是（）．

A、①② B、②④ C、①③ D、③④

查看试题解析
6. 如图，OP平分∠AOB，PC⊥OA于C，点D是OB上的动点，若PC=6cm则PD的长可以是（）．

A、3cm B、4cm C、5cm D、6 cm

查看试题解析
7. 如图，点A，B在方格纸的格点上，将线段AB先向右平移3格，再向下平移2个单位，得线段DC，点A的对应点为D，连接AD，BC，则关于四边形ABCD的对称性，下列说法正确的是（）．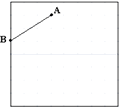

A、既是轴对称图形，又是中心对称图形 B、是中心对称图形，但不是轴对称图形 C、是轴对称图形，但不是中心对称图形 D、既不是轴对称图形，也不是中心对称图形

查看试题解析
8. 甲、乙两地去年12月前5天的日平均气温如图所示，下列描述错误的是（）

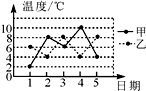A、两地气温的平均数相同 B、甲地气温的中位数是6℃ C、乙地气温的众数是4℃ D、乙地气温相对比较稳定

查看试题解析
9. 如图，正六边形 ABCDEF的中心与坐标原点O重合，其中A(-2，0)．将六边形 ABCDEF绕原点O按顺时针方向旋转2018次，每次旋转60°，则旋转后点A的对应点A'的坐标是（）．

A、(1， $\sqrt{3}$ ) B、( $\sqrt{3}$ ，1) C、(1， $- \sqrt{3}$ ) D、(-1， $\sqrt{3}$ )

查看试题解析
10. 如图，在矩形ABCD中，点A在x轴上，点B的坐标为(1，0)，且C、D两点在函数y= ${\begin{matrix} x + 1 (x \geq 0) \\ - \frac{1}{2} x + 1 (x < 0) \end{matrix}$ 的图象上，若在矩形ABCD内随机取一点，则此点取自阴影部分的概率是（）．

A、 $\frac{1}{2}$ B、 $\frac{3}{8}$ C、 $\frac{1}{4}$ D、 $\frac{1}{6}$

查看试题解析

二、填空题

11. 因式分解： $a x^{2} - a$ = ．

查看试题解析
12. 一个不透明的袋子中装有4个红球、2个黑球，它们除颜色外其余都相同，从中任意搞出3球，则事件“摸出的球至少有1个红球”是事件(填“必然”、 “随机”或“不可能”)

查看试题解析
13. 如图，DE是△ABC的中位线，若△ADE的面积为3，则△ABC的面积为．

查看试题解析
14. “若实数a，b，c满足a<b<c，则a+b<c”，能够说明该命题是假命题的一组a，b，c的值依次为．

查看试题解析
15. 如图，在□ABCD中，点E，F分别在边AD、BC上，EF=2，∠DEF=60°将四边形EFCD沿EF翻折，得到四边形EFC'D’，ED’交BC于点G，则△GEF的周长为．

查看试题解析
16. 如图，双曲线y= $\frac{k}{x}$ (x>0)经过A、B两点，若点A的横坐标为1，∠OAB=90°，且OA=AB，则k的值为．

查看试题解析

三、解答题

17. 计算： $3^{- 1} + π^{0} - \sqrt{\frac{1}{9}}$

查看试题解析
18. 如图，在△ABC中，∠A=80°，∠B=40°．

(1)、求作线段BC的垂直平分线DE，垂足为E，交AB于点D；(要求；尺规作图，保留作图痕迹，不写作法)

(2)、在(1)的条件下，连接CD，求证：AC=CD．

查看试题解析
19. 求证：对角线相等的平行四边形是矩形．(要求：画出图形，写出已知和求证，并给予证明)

查看试题解析
20. 为响应市收府关于”垃圾不落地·市区更美丽”的主题宣传活动，某校随机调查了部分学生对垃圾分类知识的掌握情况．调查选项分为“A：非常了解，B：比较了解C：了解较少，D：不了解”四种，并将调查结果绘制成以下两幅不完整的统计图．
请根据图中提供的信息，解答下列问题：

(1)、把两幅统计图补充完整；

(2)、若该校学生数1000名，根据调查结果，估计该校“非常了解”与“比较了解”的学生共有名；

(3)、已知“非常了解”的4名男生和1名女生，从中随机抽取2名向全校做垃圾分类的知识交流，请用画树状图或列表的方法，求恰好抽到1男1女的概率．

查看试题解析
21. 如图，AB是⊙O的直径，AC是弦，D 是弧BC的中点，过点D作EF垂直于直线AC，垂足为F，交AB的延长线于点E．

(1)、求证：EF是⊙O的切线；

(2)、若tanA= $\frac{4}{3}$ ，AF=6，求⊙O的半径．

查看试题解析
22. 某景区售票处规定：非节假日的票价打a折售票；节假日根据团队人数x(人)实行分段售票：若 $x \leq$ 10，则按原展价购买；若x>10，则其中10人按原票价购买，超过部分的按原那价打b折购买．某旅行社带团到该景区游览，设在非节假日的购票款为y₁元，在节假日的购票款为y₂元，y₁、y₂与x之间的函数图象如图所示．

(1)、观察图象可知：a= ， b=；

(2)、当x>10时，求y₂与x之间的函数表达式；

(3)、该旅行社在今年5月1日带甲团与5月10日(非节假日)带乙国到该景区游览，两团合计50人，共付门票款3120元，已知甲团人数超过10人，求甲团人数与乙团人数．

查看试题解析
23. 阅读：所谓勾股数就是满足方程x²+y²=z²的正整数解，即满足勾股定理的三个正整数构成的一组数．我国古代数学专著《九章算术》一书，在世界上第一次给出该方程的解为： $x = \frac{1}{2} (m^{2} - n^{2})$ ，y=mn， $z = \frac{1}{2} (m^{2} + n^{2})$ ，其中m>n>0，m、n是互质的奇数．应用：当n=5时，求一边长为12的直角三角形另两边的长．

查看试题解析
24. 已知抛物线 $y = a x^{2} + b x + c$ (a、b、c是常数， $a \neq 0$ )的对称轴为直线 $x = - 2$ ．

(1)、b=；(用含a的代数式表示)

(2)、当 $a = - 1$ 时，若关于x的方程 $a x^{2} + b x + c = 0$ 在 $- 3 < x < 1$ 的范围内有解，求c的取值范围；

(3)、若抛物线过点( $- 2$ ， $- 2$ )，当 $- 1 \leq x \leq 0$ 时，抛物线上的点到x轴距离的最大值为4，求a的值．

查看试题解析
25. 如图，在正方形ABCD中，对角线AC、BD相交于点O，E为OC上动点(与点O不重合)，作AF⊥BE，垂足为G，交BC于F，交B0于H，连接OG，CC．

(1)、求证：AH=BE；

(2)、试探究：∠AGO的度数是否为定值?请说明理由；

(3)、若OG⊥CG，BG= $\sqrt{5}$ ，求△OGC的面积．

查看试题解析