福建省龙岩市永定县金丰片2018届九年级数学中考一模试卷

试卷更新日期：2018-07-23 类型：中考模拟

进入出卷网下载

一、单选题

1. 8的立方根是（）

A、2 B、±2 C、 $\sqrt{2}$ D、4

查看试题解析
2. 如图所示的工件，其俯视图是（）

A、 B、 C、 D、

查看试题解析
3. 下列实数中的无理数是（）

A、 $\sqrt{9}$ B、π C、0 D、 $\frac{1}{3}$

查看试题解析
4. 下列各式计算正确的是（）

A、a²＋2a³＝3a⁵ B、(a²)³＝a⁵ C、a⁶÷a²＝a³ D、a·a²＝a³

查看试题解析
5. 下列国旗图案是轴对称图形但不是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
6. 如图，在△ABC中，点D，E分别在边AB，AC上，DE∥BC，若BD=2AD，则（）

A、 $\frac{A D}{A B} = \frac{1}{2}$ B、 $\frac{A E}{E C} = \frac{1}{2}$ C、 $\frac{A D}{E C} = \frac{1}{2}$ D、 $\frac{D E}{B C} = \frac{1}{2}$

查看试题解析
7. 若x+5＞0，则（）

A、x+1＜0 B、x﹣1＜0 C、 $\frac{x}{5}$ ＜﹣1 D、﹣2x＜12

查看试题解析
8. 如图， $▱ A B C D$ 中，∠B=70°，BC=6，以AD为直径的⊙O交CD于点E，则弧DE的长为（）

A、 $\frac{1}{3} π$ B、 $\frac{2}{3}$ C、 $\frac{7}{6} π$ D、 $\frac{4}{3} π$

查看试题解析
9. 设直线x=1是函数y=ax²+bx+c（a，b，c是实数，且a＜0）的图象的对称轴，（）

A、若m＞1，则（m﹣1）a+b＞0 B、若m＞1，则（m﹣1）a+b＜0 C、若m＜1，则（m﹣1）a+b＞0 D、若m＜1，则（m﹣1）a+b＜0

查看试题解析
10. 如图，数学实践活动小组要测量学校附近楼房CD的高度，在水平地面A处安置测倾器测得楼房CD顶部点D的仰角为45°，向前走20米到达A′处，测得点D的仰角为67.5°，已知测倾器AB的高度为1.6米，则楼房CD的高度约为（结果精确到0.1米， $\sqrt{2}$ ≈1.414）（）

A、34.14米 B、34.1米 C、35.7米 D、35.74米

查看试题解析

二、填空题

11. 当a，b互为相反数，则代数式a²+ab﹣2的值为．

查看试题解析
12. 在Rt△ABC中，∠C=90°，AB=2，BC= $\sqrt{3}$ ，则sin $\frac{A}{2}$ =

查看试题解析
13. 当x时，二次根式 $\sqrt{2 - x}$ 有意义.

查看试题解析
14. 若 $\frac{m - 3}{m - 1} \cdot | m | = \frac{m - 3}{m - 1}$ ，则m= ．

查看试题解析
15. 如图，在平面直角坐标系中，每个小方格的边长均为1.△AOB与△A′OB′是以原点O为位似中心的位似图形，且相似比为3：2，点A，B都在格点上，则点B′的坐标是.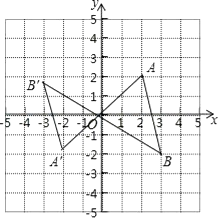

查看试题解析
16. 如图，直线y＝x＋2与反比例函数y＝ $\frac{k}{x}$ 的图象在第一象限交于点P.若OP＝ $\sqrt{10}$ ，则k的值为．

查看试题解析

三、解答题

17. 计算： $\sqrt{32} \times \sqrt{\frac{1}{2}} - {(\sqrt{3} - 2)}^{0} - | - 2 | + 2^{- 1}$ ．

查看试题解析
18. 先化简，再求值： $\frac{a^{2} - 6 a + 9}{a^{2} - 4} \cdot \frac{a + 2}{a - 3} - \frac{a - 1}{a - 2}$ ，其中 $a = - 4$ ．

查看试题解析
19. 解不等式组 ${\begin{matrix} 3 - x \geq 0 \\ 3 (1 - x) > 2 (x + 9) \end{matrix}$

查看试题解析
20. 解方程： $\frac{2 x}{x - 2} = 1 - \frac{1}{2 - x}$ ．

查看试题解析
21. 今年，我市某中学响应习总书记“足球进校园”的号召，开设了“足球大课间”活动.现需要购进100个某品牌的足球供学生使用.经调查，该品牌足球2015年单价为200元，2017年单价为162元.

(1)、求2015年到2017年该品牌足球单价平均每年降低的百分率；

(2)、选购期间发现该品牌足球在两个文体用品商店有不同的促销方案：
试问去哪个商场购买足球更优惠？

查看试题解析
22. 如图，在锐角三角形ABC中，点D，E分别在边AC，AB上，AG⊥BC于点G，AF⊥DE于点F，∠EAF=∠GAC．

(1)、求证：△ADE∽△ABC；

(2)、若AD=3，AB=5，求 $\frac{A F}{A G}$ 的值．

查看试题解析
23. 主题班会课上，王老师出示了如图所示的一幅漫画，经过同学们的一番热议，达成以下四个观点：
A.放下自我，彼此尊重； B.放下利益，彼此平衡；
C.放下性格，彼此成就； D.合理竞争，合作双赢.
要求每人选取其中一个观点写出自己的感悟.根据同学们的选择情况，小明绘制了下面两幅不完整的图表，请根据图表中提供的信息，解答下列问题：
观点
频数
频率
A
a
0.2
B
12
0.24
C
8
b
D
20
0.4

(1)、参加本次讨论的学生共有人；

(2)、表中a= ， b=；

(3)、将条形统计图补充完整；

(4)、现准备从A，B，C，D四个观点中任选两个作为演讲主题，请用列表或画树状图的方法求选中观点D（合理竞争，合作双赢）的概率.

查看试题解析
24. 如图，点C在以AB为直径的⊙O上，AD与过点C的切线垂直，垂足为点D，AD交⊙O于点E．

(1)、求证：AC平分∠DAB；

(2)、连接BE交AC于点F，若cos∠CAD＝ $\frac{4}{5}$ ，求 $\frac{A F}{F C}$ 的值．

查看试题解析
25. 如图1，在平面直角坐标系中，抛物线y＝x²－4x－5与x轴分别交于A、B（A在B的左边），与y轴交于点C，直线AP与y轴正半轴交于点M，交抛物线于点P，直线AQ与y轴负半轴交于点N，交抛物线于点Q，且OM＝ON，过P、Q作直线l

(1)、探究与猜想：
① 取点M(0，1)，直接写出直线l的解析式；
取点M(0，2)，直接写出直线l的解析式.
② 猜想：
我们猜想直线l的解析式y＝kx＋b中，k总为定值，定值k为，请取M的纵坐标为n，验证你的猜想

(2)、如图2，连接BP、BQ．若△ABP的面积等于△ABQ的面积的3倍，试求出直线l的解析式

查看试题解析

观点	频数	频率
A	a	0.2
B	12	0.24
C	8	b
D	20	0.4