福建省福州市福清市2018届数学中考模拟试卷
试卷更新日期：2018-07-23 类型：中考模拟
一、单选题
-
1. 下列函数的解析式中是一次函数的是（ ）A、y= B、y= x+1 C、y=x2+1 D、y=2. 在下列性质中，平行四边形不一定具有的是（ ）A、对边相等 B、对边平行 C、对角互补 D、内角和为360°3. 在一次数学阶段考试中，某小组7名同学的成绩（单位：分）分别是65，80，70，90，95，100，70，这组数据的众数是（ ）A、90 B、85 C、80 D、704. 甲，乙两个样本的容量相同，甲样本的方差为0.102，乙样本的方差是0.06，那么（ ）A、甲的波动比乙的波动大 B、乙的波动比甲的波动大 C、甲，乙的波动大小一样 D、甲，乙的波动大小无法确定5. 已知一次函数y=（m﹣1）x﹣4的图象经过（2，4），则m的值为（ ）A、7 B、5 C、8 D、26. 一次函数y=2x+1的图象不经过（ ）A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 下图是某学校全体教职工年龄的频数分布直方图（统计中采用“上限不在内”的原则，如年龄为36岁统计在36≤x＜38小组，而不在34≤x＜36小组），根据图形提供的信息，下列说法中错误的是（ ）
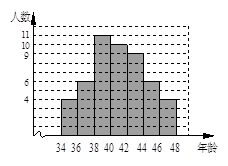A、该学校教职工总人数是50人 B、年龄在40≤x＜42小组的教职工人数占该学校总人数的20% C、教职工年龄的中位数一定落在40≤x＜42这一组 D、教职工年龄的众数一定在38≤x＜40这一组二、填空题
-
8. 正比例函数y=﹣5x中，y随着x的增大而 ．9. 已知函数y=﹣x+3，当x=时，函数值为0．10. 在矩形ABCD中，再增加条件（只需填一个）可使矩形ABCD成为正方形．11. 有一组数据如下：3，a，4，6，7，它们的平均数是5，那么a= ．12. 将直线y= x向下平移3个单位，得到直线 ．13. 某招聘考试分笔试和面试两种．其中笔试按60%、面试按40%计算加权平均数作为总成绩．小明笔试成绩为90分．面试成绩为85分，那么小明的总成绩为分．
14. 为了培养学生勤俭节约的意识，从小养成良好的生活习惯．某校随机抽查部分初中生对勤俭节约的态度（态度分为：赞成、无所谓、反对），并对抽查对象的态度绘制成了图1和图2两个统计图（统计图不完整），请根据图中的信息解答下列问题：
(1)、此次共抽查名学生；(2)、持反对意见的学生人数占整体的 %，无所谓意见的学生人数占整体的 %；(3)、估计该校1200名初中生中，大约有名学生持反对态度．三、解答题
-
15. 已知：函数y=（1﹣3k）x+2k﹣1，试回答：(1)、k为何值时，图象过原点？
(2)、k为何值时，y随x的增大而增大？
16. 已知样本数据为1，2，3，4，5，求这个样本的：(1)、平均数 ；(2)、方差S2 ． （提示：S2= [x1﹣ ）2+（x2﹣ ）2+（x3﹣ ）2+（x4﹣ ）2+（x5﹣ ）2]）17. 已知一次函数的图象经过A(－2，－3)，B(1，3)两点.(1)、求这个一次函数的解析式；(2)、试判断点P(－1，1)是否在这个一次函数的图象上(3)、求此函数与x轴、y轴围成的三角形的面积.18. 在矩形ABCD中，两条对角线相交于O，∠AOB=60°，AB=2，求AD的长。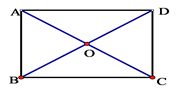
19. 如图，在矩形ABCD中，E、F分别是边AB、CD的中点，连接AF，CE．
(1)、求证：△BEC≌△DFA；(2)、求证：四边形AECF是平行四边形．20. 某商场欲购进果汁饮料和碳酸饮料共50箱，果汁饮料毎箱进价为55元，售价为63元；碳酸饮料毎箱进价为36元，售价为42元；设购进果汁饮料x箱（x为正整数），且所购进的两种饮料能全部卖出，获得的总利润为W元（注，总利润=总售价﹣总进价），
(1)、设商场购进碳酸饮料y箱，直接写出y与x的函数关系式；
(2)、求总利润W关于x的函数关系式；
(3)、如果购进两种饮料的总费用不超过2000元，那么该商场如何进货才能获利最多？并求出最大利润．
21. 如图，直线L：y=- x+2与x轴、y轴分别交于A、B两点，在y轴上有一点C（0，4），动点M从A点以每秒1个单位的速度沿x轴向左移动．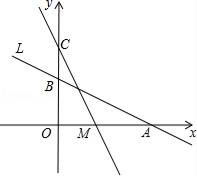
(1)、求A、B两点的坐标；
(2)、求△COM的面积S与M的移动时间t之间的函数关系式；
(3)、当t为何值时△COM≌△AOB，并求此时M点的坐标．