安徽省合肥市庐阳区2018届九年级数学中考一模试卷
试卷更新日期:2018-07-23 类型:中考模拟
一、单选题
-
1. 计算(﹣2x2)3的结果是( )A、﹣8x6 B、﹣6x6 C、﹣8x5 D、﹣6x52. 如图所示的工件,其俯视图是( )
 A、
A、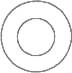 B、
B、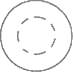 C、
C、 D、
D、 3. 2018年3月5日,李克强总理在政府工作报告中指出,过去五年农村贫困人口脱贫6800万,脱贫攻坚取得阶段性胜利,6800万用科学记数法表示为( )A、6800×104 B、6.8×104 C、6.8×107 D、0.68×1084. 不等式组 的解集在数轴上表示正确的是( )A、
3. 2018年3月5日,李克强总理在政府工作报告中指出,过去五年农村贫困人口脱贫6800万,脱贫攻坚取得阶段性胜利,6800万用科学记数法表示为( )A、6800×104 B、6.8×104 C、6.8×107 D、0.68×1084. 不等式组 的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、 5. 如图,把一块含有45°的直角三角形的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是( )
5. 如图,把一块含有45°的直角三角形的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是( )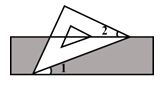 A、15° B、20° C、25° D、30°6. 下列关于x的一元二次方程有实数根的是( )A、x2+1=0 B、x2+x+1=0 C、x2﹣x+1=0 D、x2﹣x﹣1=07. 某企业因春节放假,二月份产值比一月份下降20%,春节后生产呈现良好上升势头,四月份比一月份增长15%,设三、四月份的月平均增长率为x,则下列方程正确的是( )A、(1﹣20%)(1+x)2=1+15% B、(1+15%%)(1+x)2=1﹣20% C、2(1﹣20%)(1+x)=1+15% D、2(1+15%)(1+x)=1﹣20%8. 在同一平面坐标系中,函数y=mx+m和y=﹣mx2+2x+2(m是常数,且m≠0)的图象可能是( )A、
A、15° B、20° C、25° D、30°6. 下列关于x的一元二次方程有实数根的是( )A、x2+1=0 B、x2+x+1=0 C、x2﹣x+1=0 D、x2﹣x﹣1=07. 某企业因春节放假,二月份产值比一月份下降20%,春节后生产呈现良好上升势头,四月份比一月份增长15%,设三、四月份的月平均增长率为x,则下列方程正确的是( )A、(1﹣20%)(1+x)2=1+15% B、(1+15%%)(1+x)2=1﹣20% C、2(1﹣20%)(1+x)=1+15% D、2(1+15%)(1+x)=1﹣20%8. 在同一平面坐标系中,函数y=mx+m和y=﹣mx2+2x+2(m是常数,且m≠0)的图象可能是( )A、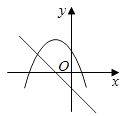 B、
B、 C、
C、 D、
D、 9. 如图,已知菱形ABCD的周长为16,面积为 ,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为( )
9. 如图,已知菱形ABCD的周长为16,面积为 ,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为( )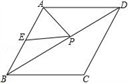 A、2 B、2 C、4 D、4
A、2 B、2 C、4 D、4二、填空题
-
10. 分解因式:a3﹣2a2+a= .11. 如图,正五边形ABCDE的边长为2,分别以点C、D为圆心,CD长为半径画弧,两弧交于点F,则弧BF 的长为 .
 12. 矩形纸片ABCD中,已知AD=8,AB=6,E是边BC上的点,以AE为折痕折叠纸片,使点B落在点F处,连接FC,当△EFC为直角三角形时,BE的长为 .
12. 矩形纸片ABCD中,已知AD=8,AB=6,E是边BC上的点,以AE为折痕折叠纸片,使点B落在点F处,连接FC,当△EFC为直角三角形时,BE的长为 .三、解答题
-
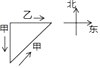
13. 计算:( )﹣2﹣ +( ﹣4)0﹣ cos45°.14. 《九章算术》“勾股”章有一题:“今有二人同所立,甲行率七,乙行率三.乙东行,甲南行十步而斜东北与乙会.问甲乙行各几何”.大意是说,已知甲、乙二人同时从同一地点出发,甲的速度为7,乙的速度为3.乙一直向东走,甲先向南走10步,后又斜向北偏东方向走了一段后与乙相遇.那么相遇时,甲、乙各走了多远?
 15. 如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4),请解答下列问题:
15. 如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4),请解答下列问题:
①画出△ABC关于x轴对称的△A1B1C1 , 并写出点A1的坐标.
②画出△A1B1C1绕原点O旋转180°后得到的△A2B2C2 , 并写出点A2的坐标.
16. 观察下面的点阵图和相应的等式,探究其中的规律:(1)、认真观察,并在④后面的横线上写出相应的等式.
①1=1 ②1+2= =3 ③1+2+3= =6 ④
(2)、结合(1)观察下列点阵图,并在⑤后面的横线上写出相应的等式.
1=12②1+3=22③3+6=32④6+10=42⑤
(3)、通过猜想,写出(2)中与第n个点阵相对应的等式 .17. 如图,用细线悬挂一个小球,小球在竖直平面内的A、C两点间来回摆动,A点与地面距离AN=14cm,小球在最低点B时,与地面距离BM=5cm,∠AOB=66°,求细线OB的长度.(参考数据:sin66°≈0.91,cos66°≈0.40,tan66°≈2.25)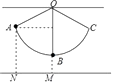 18. 已知:如图,在半径为4的⊙O中,AB、CD是两条直径,M为OB的中点,CM的延长线交⊙O于点E,且EM>MC.连接DE,DE= .
18. 已知:如图,在半径为4的⊙O中,AB、CD是两条直径,M为OB的中点,CM的延长线交⊙O于点E,且EM>MC.连接DE,DE= . (1)、求证:AM•MB=EM•MC;(2)、求EM的长;(3)、求sin∠EOB的值.19. 为大力弘扬“奉献、友爱、互助、进步”的志愿服务精神,传播“奉献他人、提升自我”的志愿服务理念,合肥市某中学利用周末时间开展了“助老助残、社区服务、生态环保、网络文明”四个志愿服务活动(每人只参加一个活动),九年级某班全班同学都参加了志愿服务,班长为了解志愿服务的情况,收集整理数据后,绘制以下不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
(1)、求证:AM•MB=EM•MC;(2)、求EM的长;(3)、求sin∠EOB的值.19. 为大力弘扬“奉献、友爱、互助、进步”的志愿服务精神,传播“奉献他人、提升自我”的志愿服务理念,合肥市某中学利用周末时间开展了“助老助残、社区服务、生态环保、网络文明”四个志愿服务活动(每人只参加一个活动),九年级某班全班同学都参加了志愿服务,班长为了解志愿服务的情况,收集整理数据后,绘制以下不完整的统计图,请你根据统计图中所提供的信息解答下列问题: (1)、请把折线统计图补充完整;
(1)、请把折线统计图补充完整;
(2)、求扇形统计图中,网络文明部分对应的圆心角的度数;
(3)、小明和小丽参加了志愿服务活动,请用树状图或列表法求出他们参加同一服务活动的概率.20. 某旅行社推出一条成本价位500元/人的省内旅游线路,游客人数y(人/月)与旅游报价x(元/人)之间的关系为y=﹣x+1300,已知:旅游主管部门规定该旅游线路报价在800元/人~1200元/人之间.
(1)、要将该旅游线路每月游客人数控制在200人以内,求该旅游线路报价的取值范围;
(2)、求经营这条旅游线路每月所需要的最低成本;
(3)、当这条旅游线路的旅游报价为多少时,可获得最大利润?最大利润是多少?
21. 已知四边形ABCD中,AB=AD,对角线AC平分∠DAB,过点C作CE⊥AB于点E,点F为AB上一点,且EF=EB,连接DF.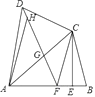 (1)、求证:CD=CF;(2)、连接DF,交AC于点G,求证:△DGC∽△ADC;(3)、若点H为线段DG上一点,连接AH,若∠ADC=2∠HAG,AD=3,DC=2,求 的值.
(1)、求证:CD=CF;(2)、连接DF,交AC于点G,求证:△DGC∽△ADC;(3)、若点H为线段DG上一点,连接AH,若∠ADC=2∠HAG,AD=3,DC=2,求 的值.