中考备考专题复习：变式猜想问题-在线组卷题库

1.

如图1，在△ABC和△EDC中，AC=CE=CB=CD；∠ACB=∠DCE=90°，AB与CE交于F，ED与AB，BC，分别交于M，H．

(1)、求证：CF=CH；

(2)、如图2，△ABC不动，将△EDC绕点C旋转到∠BCE=45°时，试判断四边形ACDM是什么四边形？并证明你的结论．

查看试题解析

2.

如图1所示，在正方形ABCD和正方形CGEF中，点B、C、G在同一条直线上，M是线段AE的中点，DM的延长线交EF于点N，连接FM，易证：DM=FM，DM⊥FM（无需写证明过程）

(1)、如图2，当点B、C、F在同一条直线上，DM的延长线交EG于点N，其余条件不变，试探究线段DM与FM有怎样的关系？请写出猜想，并给予证明；

(2)、

如图3，当点E、B、C在同一条直线上，DM的延长线交CE的延长线于点N，其余条件不变，探究线段DM与FM有怎样的关系？请直接写出猜想．

查看试题解析

3.

已知四边形ABCD是正方形，等腰直角△AEF的直角顶点E在直线BC上（不与点B，C重合），FM⊥AD，交射线AD于点M．

(1)、当点E在边BC上，点M在边AD的延长线上时，如图①，求证：AB+BE=AM；

（提示：延长MF，交边BC的延长线于点H．）

(2)、当点E在边CB的延长线上，点M在边AD上时，如图②；当点E在边BC的延长线上，点M在边AD上时，如图③．请分别写出线段AB，BE，AM之间的数量关系，不需要证明；

(3)、在（1），（2）的条件下，若BE=

\sqrt{3}

， ∠AFM=15°，则AM= .

查看试题解析

4.

（1）问题如图1，在四边形ABCD中，点P为AB上一点，∠DPC=∠A=∠B=90°

(1)、求证：AD•BC=AP•BP

(2)、

探究如图2，在四边形ABCD中，点P为AB上一点，当∠DPC=∠A=∠B=θ时，上述结论是否依然成立？说明理由．

(3)、

应用请利用（1）（2）获得的经验解决问题：

如图3，在△ABD中，AB=6，AD=BD=5，点P以每秒1个单位长度的速度，由点A出发，沿边AB向点B运动，且满足∠DPC=∠A，设点P的运动时间为t（秒），当以D为圆心，以DC为半径的圆与AB相切时，求t的值．

查看试题解析

5.

如图1，在△ABC中，∠ACB=90°，AC=BC，∠EAC=90°，点M为射线AE上任意一点（不与A重合），连接CM，将线段CM绕点C按顺时针方向旋转90°得到线段CN，直线NB分别交直线CM、射线AE于点F、D．

(1)、直接写出∠NDE的度数.

(2)、

如图2、图3，当∠EAC为锐角或钝角时，其他条件不变，（1）中的结论是否发生变化？如果不变，选取其中一种情况加以证明；如果变化，请说明理由.

(3)、

如图4，若∠EAC=15°，∠ACM=60°，直线CM与AB交于G，BD= $\frac{\sqrt{6} + \sqrt{2}}{2}$ ，其他条件不变，求线段AM的长．

查看试题解析

6. 阅读材料：

在一个三角形中，各边和它所对角的正弦的比相等， $\frac{a}{\sin A}$ = $\frac{b}{\sin B}$ = $\frac{c}{\sin C}$ ，利用上述结论可以求解如下题目：

在△ABC中，∠A、∠B、∠C的对边分别为a，b，c．若∠A=45°，∠B=30°，a=6，求b．

解：在△ABC中，∵ $\frac{a}{\sin A}$ = $\frac{b}{\sin B}$ ∴b= $\frac{a \sin B}{\sin A}$ = $\frac{6 \sin 30 °}{\sin 45 °}$ = $\frac{6 \times \frac{1}{2}}{\frac{\sqrt{2}}{2}}$ =3 $\sqrt{2}$ ．

理解应用：

如图，甲船以每小时30 $\sqrt{2}$ 海里的速度向正北方向航行，当甲船位于A₁处时，乙船位于甲船的北偏西105°方向的B₁处，且乙船从B₁处按北偏东15°方向匀速直线航行，当甲船航行20分钟到达A₂时，乙船航行到甲船的北偏西120°方向的B₂处，此时两船相距10 $\sqrt{2}$ 海里．

(1)、判断△A₁A₂B₂的形状，并给出证明

(2)、求乙船每小时航行多少海里？

查看试题解析

7.

如图1，在正方形ABCD的外侧，作两个等边三角形ADE和DCF，连接AF，BE

(1)、请判断：AF与BE的数量关系是，位置关系是 .

(2)、如图2，若将条件“两个等边三角形ADE和DCF”变为“两个等腰三角形ADE和DCF，且EA=ED=FD=FC”，第（1）问中的结论是否仍然成立？请作出判断并给予说明

(3)、若三角形ADE和DCF为一般三角形，且AE=DF，ED=FC，第（1）问中的结论都能成立吗？请直接写出你的判断.

查看试题解析

8.

已知正方形ABCD的边长为1，点P为正方形内一动点，若点M在AB上，且满足△PBC∽△PAM，延长BP交AD于点N，连结CM．

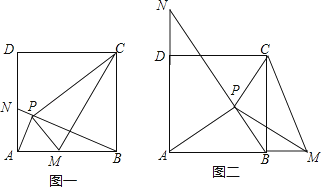(1)、如图一，若点M在线段AB上，求证：AP⊥BN；AM=AN；

(2)、①如图二，在点P运动过程中，满足△PBC∽△PAM的点M在AB的延长线上时，AP⊥BN和AM=AN是否成立？（不需说明理由）

②是否存在满足条件的点P，使得PC= $\frac{1}{2}$ ？请说明理由．

查看试题解析

9.

如图1，在正方形ABCD中，点E，F分别是边BC，AB上的点，且CE=BF．连接DE，过点E作EG⊥DE，使EG=DE，连接FG，FC．

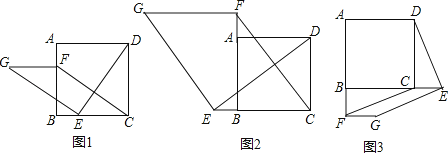(1)、请判断：FG与CE的数量关系是，位置关系是；

(2)、如图2，若点E，F分别是边CB，BA延长线上的点，其它条件不变，（1）中结论是否仍然成立？请作出判断并给予证明；

(3)、如图3，若点E，F分别是边BC，AB延长线上的点，其它条件不变，（1）中结论是否仍然成立？请直接写出你的判断．

查看试题解析

10.

△ABC中，∠BAC=90°，AB=AC，点D为直线BC上一动点（点D不与B，C重合），以AD为边在AD右侧作正方形ADEF，连接CF．

(1)、观察猜想

如图1，当点D在线段BC上时，

①BC与CF的位置关系为：．

②BC，CD，CF之间的数量关系为：；（将结论直接写在横线上）

(2)、数学思考

如图2，当点D在线段CB的延长线上时，结论①，②是否仍然成立？若成立，请给予证明；若不成立，请你写出正确结论再给予证明．

(3)、拓展延伸

如图3，当点D在线段BC的延长线上时，延长BA交CF于点G，连接GE．若已知AB=2 $\sqrt{2}$ ，CD= $\frac{1}{4}$ BC，请求出GE的长．

查看试题解析

11.

问题引入：

(1)、如图①，在△ABC中，点O是∠ABC和∠ACB平分线的交点，若∠A=α，则∠BOC=（用α表示）；如图②，∠CBO=

\frac{1}{3}

∠ABC，∠BCO=

\frac{1}{3}

∠ACB，∠A=α，则∠BOC=（用α表示）拓展研究：

(2)、如图③，∠CBO=

\frac{1}{3}

∠DBC，∠BCO=

\frac{1}{3}

∠ECB，∠A=α，请猜想∠BOC=（用α表示），并说明理由．

类比研究：

(3)、BO、CO分别是△ABC的外角∠DBC、∠ECB的n等分线，它们交于点O，∠CBO=

\frac{1}{n}

∠DBC，∠BCO=

\frac{1}{n}

∠ECB，∠A=α，请猜想∠BOC= ．

查看试题解析

12.

已知四边形ABCD是菱形，AB=4，∠ABC=60°，∠EAF的两边分别与射线CB，DC相交于点E，F，且∠EAF=60°．

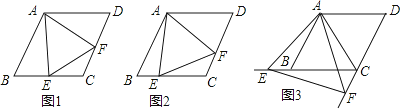(1)、如图1，当点E是线段CB的中点时，直接写出线段AE，EF，AF之间的数量关系；

(2)、如图2，当点E是线段CB上任意一点时（点E不与B、C重合），求证：BE=CF；

(3)、如图3，当点E在线段CB的延长线上，且∠EAB=15°时，求点F到BC的距离．

查看试题解析

13.

在△ABC中，AB=AC，∠BAC=2∠DAE=2α．

(1)、如图1，若点D关于直线AE的对称点为F，求证：△ADF∽△ABC；

(2)、如图2，在（1）的条件下，若α=45°，求证：DE²=BD²+CE²；

(3)、如图3，若α=45°，点E在BC的延长线上，则等式DE²=BD²+CE²还能成立吗？请说明理由．

查看试题解析

14.

如图1，△ABC是等腰直角三角形，∠BAC=90°，AB=AC，四边形ADEF是正方形，点B、C分别在边AD、AF上，此时BD=CF，BD⊥CF成立．

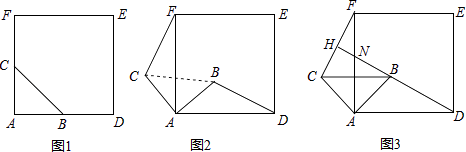(1)、当△ABC绕点A逆时针旋转θ（0°＜θ＜90°）时，如图2，BD=CF成立吗？若成立，请证明，若不成立，请说明理由；

(2)、当△ABC绕点A逆时针旋转45°时，如图3，延长BD交CF于点H．

①求证：BD⊥CF；

②当AB=2，AD=3 $\sqrt{2}$ 时，求线段DH的长．

查看试题解析

15.

如图1，2，3分别以△ABC的AB和AC为边向△ABC外作正三角形（等边三角形）、正四边形（正方形）、正五边形，BE和CD相交于点O．

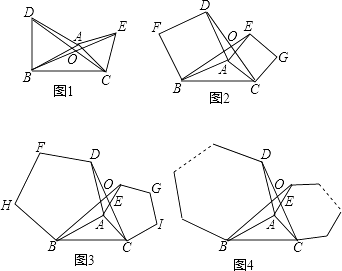(1)、在图1中，求证：△ABE≌△ADC．

(2)、由（1）证得△ABE≌△ADC，由此可推得在图1中∠BOC=120°，请你探索在图2中，∠BOC的度数，并说明理由或写出证明过程．

(3)、填空：在上述（1）（2）的基础上可得在图3中∠BOC=（填写度数）．

(4)、由此推广到一般情形（如图4），分别以△ABC的AB和AC为边向△ABC外作正n边形，BE和CD仍相交于点O，猜想得∠BOC的度数为（用含n的式子表示）．

查看试题解析

16.

在学习了图形的旋转知识后，数学兴趣小组的同学们又进一步对图形旋转前后的线段之间、角之间的关系进行了探究．

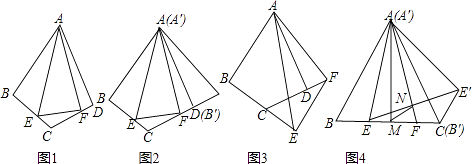
（一）尝试探究

如图1，在四边形ABCD中，AB=AD，∠BAD=60°，∠ABC=∠ADC=90°，点E、F分别在线段BC、CD上，∠EAF=30°，连接EF．

(1)、如图2，将△ABE绕点A逆时针旋转60°后得到△A′B′E′（A′B′与AD重合），请直接写出∠E′AF=度，线段BE、EF、FD之间的数量关系为．

(2)、如图3，当点E、F分别在线段BC、CD的延长线上时，其他条件不变，请探究线段BE、EF、FD之间的数量关系，并说明理由．

查看试题解析

17. 阅读下面材料：

小明遇到这样一个问题：如图1，△ABC中，AB=AC，点D在BC边上，∠DAB=∠ABD，BE⊥AD，垂足为E，求证：BC=2AE．

小明经探究发现，过点A作AF⊥BC，垂足为F，得到∠AFB=∠BEA，从而可证△ABF≌△BAE（如图2），使问题得到解决．

(1)、根据阅读材料回答：△ABF与△BAE全等的条件是 AAS（填“SSS”、“SAS”、“ASA”、“AAS”或“HL”中的一个）

参考小明思考问题的方法，解答下列问题：

(2)、如图3，△ABC中，AB=AC，∠BAC=90°，D为BC的中点，E为DC的中点，点F在AC的延长线上，且∠CDF=∠EAC，若CF=2，求AB的长；

(3)、如图4，△ABC中，AB=AC，∠BAC=120°，点D、E分别在AB、AC边上，且AD=kDB（其中0＜k＜

\frac{\sqrt{3}}{3}

），∠AED=∠BCD，求

\frac{A E}{E C}

的值（用含k的式子表示）．

查看试题解析

中考备考专题复习：变式猜想问题

一、综合题