中考备考专题复习：开放探究问题

试卷更新日期：2017-02-08 类型：二轮复习

进入出卷网下载

一、单选题

1.
如图，四个实数m，n，p，q在数轴上对应的点分别为M，N，P，Q，若n+q=0，则m，n，p，q四个实数中，绝对值最大的一个是（　　）

A、p B、q C、m D、n

查看试题解析
2. n是整数，式子 $\frac{1}{8}$ [1﹣（﹣1）ⁿ]（n²﹣1）计算的结果（　　）

A、是0 B、总是奇数 C、总是偶数 D、可能是奇数也可能是偶数

查看试题解析
3. 抛物线y=x²+bx+c（其中b，c是常数）过点A（2，6），且抛物线的对称轴与线段y=0（1≤x≤3）有交点，则c的值不可能是（　　）

A、4 B、6 C、8 D、10

查看试题解析

二、填空题

4.
如图，△ABC中，AD⊥BC，CE⊥AB，垂足分别为D、E，AD、CE交于点H，请你添加一个适当的条件：，使△AEH≌△CEB．

查看试题解析
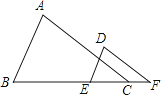
5.
如图，已知∠A=∠D，要使△ABC∽△DEF，还需添加一个条件，你添加的条件是．（只需写一个条件，不添加辅助线和字母）

查看试题解析

三、综合题

6.
如图，正方形ABCD的对角线相交于点O，点M，N分别是边BC，CD上的动点（不与点B，C，D重合），AM，AN分别交BD于点E，F，且∠MAN始终保持45°不变．

(1)、求证： $\frac{A F}{A M}$ = $\frac{\sqrt{2}}{2}$ ；

(2)、求证：AF⊥FM；

(3)、请探索：在∠MAN的旋转过程中，当∠BAM等于多少度时，∠FMN=∠BAM？写出你的探索结论，并加以证明．

查看试题解析
7.
已知正方形ABCD的边长为1，点P为正方形内一动点，若点M在AB上，且满足△PBC∽△PAM，延长BP交AD于点N，连结CM．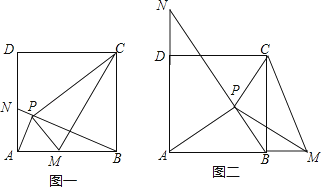

(1)、如图一，若点M在线段AB上，求证：AP⊥BN；AM=AN；

(2)、①如图二，在点P运动过程中，满足△PBC∽△PAM的点M在AB的延长线上时，AP⊥BN和AM=AN是否成立？（不需说明理由）
②是否存在满足条件的点P，使得PC= $\frac{1}{2}$ ？请说明理由．

查看试题解析
8.
如图1，在正方形ABCD中，点E，F分别是边BC，AB上的点，且CE=BF．连接DE，过点E作EG⊥DE，使EG=DE，连接FG，FC．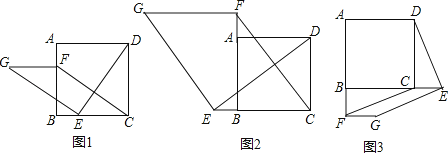

(1)、请判断：FG与CE的数量关系是，位置关系是；

(2)、如图2，若点E，F分别是边CB，BA延长线上的点，其它条件不变，（1）中结论是否仍然成立？请作出判断并给予证明；

(3)、如图3，若点E，F分别是边BC，AB延长线上的点，其它条件不变，（1）中结论是否仍然成立？请直接写出你的判断．

查看试题解析
9.
问题引入：

(1)、如图①，在△ABC中，点O是∠ABC和∠ACB平分线的交点，若∠A=α，则∠BOC=（用α表示）；如图②，∠CBO= $\frac{1}{3}$ ∠ABC，∠BCO= $\frac{1}{3}$ ∠ACB，∠A=α，则∠BOC=（用α表示）拓展研究：

(2)、如图③，∠CBO= $\frac{1}{3}$ ∠DBC，∠BCO= $\frac{1}{3}$ ∠ECB，∠A=α，请猜想∠BOC=（用α表示），并说明理由．
类比研究：

(3)、BO、CO分别是△ABC的外角∠DBC、∠ECB的n等分线，它们交于点O，∠CBO= $\frac{1}{n}$ ∠DBC，∠BCO= $\frac{1}{n}$ ∠ECB，∠A=α，请猜想∠BOC= ．

查看试题解析
10.
已知四边形ABCD是菱形，AB=4，∠ABC=60°，∠EAF的两边分别与射线CB，DC相交于点E，F，且∠EAF=60°．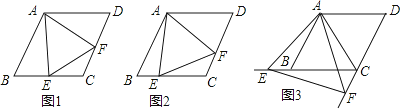

(1)、如图1，当点E是线段CB的中点时，直接写出线段AE，EF，AF之间的数量关系；

(2)、如图2，当点E是线段CB上任意一点时（点E不与B、C重合），求证：BE=CF；

(3)、如图3，当点E在线段CB的延长线上，且∠EAB=15°时，求点F到BC的距离．

查看试题解析
11.
如图，△ABC和△BEC均为等腰直角三角形，且∠ACB=∠BEC=90°，AC=4 $\sqrt{2}$ ，点P为线段BE延长线上一点，连接CP以CP为直角边向下作等腰直角△CPD，线段BE与CD相交于点F

(1)、求证： $\frac{P C}{C D} = \frac{C E}{C B}$ ；

(2)、连接BD，请你判断AC与BD有什么位置关系？并说明理由；

(3)、设PE=x，△PBD的面积为S，求S与x之间的函数关系式．

查看试题解析
12.
如图1，△ABC是等腰直角三角形，∠BAC=90°，AB=AC，四边形ADEF是正方形，点B、C分别在边AD、AF上，此时BD=CF，BD⊥CF成立．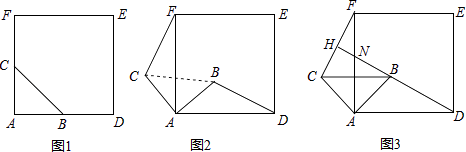

(1)、当△ABC绕点A逆时针旋转θ（0°＜θ＜90°）时，如图2，BD=CF成立吗？若成立，请证明，若不成立，请说明理由；

(2)、当△ABC绕点A逆时针旋转45°时，如图3，延长BD交CF于点H．
①求证：BD⊥CF；
②当AB=2，AD=3 $\sqrt{2}$ 时，求线段DH的长．

查看试题解析
13.
如图，已知一个直角三角形纸片ACB，其中∠ACB=90°，AC=4，BC=3，E、F分别是AC、AB边上点，连接EF．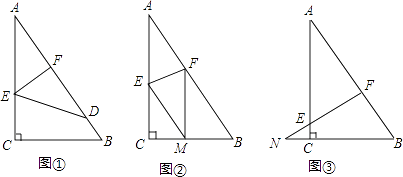

(1)、图①，若将纸片ACB的一角沿EF折叠，折叠后点A落在AB边上的点D处，且使S_四边形_ECBF=3S_△_EDF ，求AE的长；

(2)、如图②，若将纸片ACB的一角沿EF折叠，折叠后点A落在BC边上的点M处，且使MF∥CA．
①试判断四边形AEMF的形状，并证明你的结论；
②求EF的长；

(3)、如图③，若FE的延长线与BC的延长线交于点N，CN=1，CE= $\frac{4}{7}$ ，求 $\frac{A F}{B F}$ 的值．

查看试题解析
14.
如图1，在正方形ABCD内作∠EAF=45°，AE交BC于点E，AF交CD于点F，连接EF，过点A作AH⊥EF，垂足为H．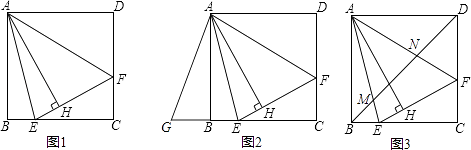

(1)、如图2，将△ADF绕点A顺时针旋转90°得到△ABG．
①求证：△AGE≌△AFE；
②若BE=2，DF=3，求AH的长．

(2)、如图3，连接BD交AE于点M，交AF于点N．请探究并猜想：线段BM，MN，ND之间有什么数量关系？并说明理由．

查看试题解析
15.
在平面直角坐标系中，O为原点，点A（4，0），点B（0，3），把△ABO绕点B逆时针旋转，得△A′BO′，点A，O旋转后的对应点为A′，O′，记旋转角为α．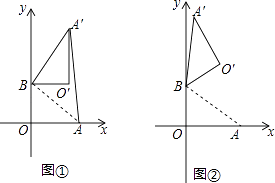

(1)、如图①，若α=90°，求AA′的长；

(2)、如图②，若α=120°，求点O′的坐标；

(3)、在（2）的条件下，边OA上的一点P旋转后的对应点为P′，当O′P+BP′取得最小值时，求点P′的坐标（直接写出结果即可）

查看试题解析
16. 如图，在△ABC中，∠C=90°，∠BAC的平分线交BC于点D，DE⊥AD，交AB于点E，AE为⊙O的直径

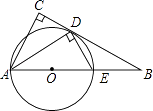(1)、判断BC与⊙O的位置关系，并证明你的结论；

(2)、求证：△ABD∽△DBE；

(3)、若cosB= $\frac{2 \sqrt{2}}{3}$ ，AE=4，求CD．

查看试题解析
17.
如图，在矩形ABCD中，AB=10，AD=6，点M为AB上的一动点，将矩形ABCD沿某一直线对折，使点C与点M重合，该直线与AB（或BC）、CD（或DA）分别交于点P、Q

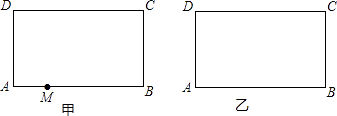(1)、用直尺和圆规在图甲中画出折痕所在直线（不要求写画法，但要求保留作图痕迹）

(2)、如果PQ与AB、CD都相交，试判断△MPQ的形状并证明你的结论；

(3)、设AM=x，d为点M到直线PQ的距离，y=d² ，
①求y关于x的函数解析式，并指出x的取值范围；
②当直线PQ恰好通过点D时，求点M到直线PQ的距离．

查看试题解析
18.
如图1，抛物线y=﹣ $\frac{3}{5}$ [（x﹣2）²+n]与x轴交于点A（m﹣2，0）和B（2m+3，0）（点A在点B的左侧），与y轴交于点C，连结BC．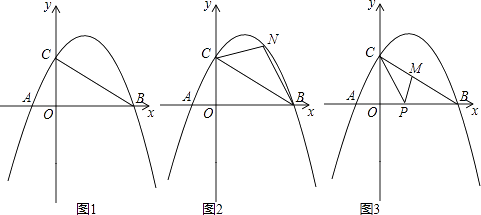

(1)、求m、n的值；

(2)、如图2，点N为抛物线上的一动点，且位于直线BC上方，连接CN、BN．求△NBC面积的最大值；

(3)、如图3，点M、P分别为线段BC和线段OB上的动点，连接PM、PC，是否存在这样的点P，使△PCM为等腰三角形，△PMB为直角三角形同时成立？若存在，求出点P的坐标；若不存在，请说明理由．

查看试题解析