中考备考专题复习：存在性问题-在线组卷题库

1.

在平面直角坐标系中，点O为原点，点A的坐标为（﹣6，0）．如图1，正方形OBCD的顶点B在x轴的负半轴上，点C在第二象限．现将正方形OBCD绕点O顺时针旋转角α得到正方形OEFG．

(1)、如图2，若α=60°，OE=OA，求直线EF的函数表达式．

(2)、若α为锐角，tanα=

\frac{1}{2}

，当AE取得最小值时，求正方形OEFG的面积．

(3)、当正方形OEFG的顶点F落在y轴上时，直线AE与直线FG相交于点P，△OEP的其中两边之比能否为

\sqrt{2}

：1？若能，求点P的坐标；若不能，试说明理由

查看试题解析

2.

如图，在平面直角坐标系中，直线y=﹣2x+10与x轴，y轴相交于A，B两点，点C的坐标是（8，4），连接AC，BC．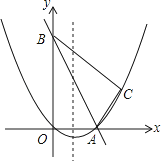

(1)、求过O，A，C三点的抛物线的解析式，并判断△ABC的形状；

(2)、动点P从点O出发，沿OB以每秒2个单位长度的速度向点B运动；同时，动点Q从点B出发，沿BC以每秒1个单位长度的速度向点C运动．规定其中一个动点到达端点时，另一个动点也随之停止运动．设运动时间为t秒，当t为何值时，PA=QA？

(3)、在抛物线的对称轴上，是否存在点M，使以A，B，M为顶点的三角形是等腰三角形？若存在，求出点M的坐标；若不存在，请说明理由．

查看试题解析

3.

已知抛物线C：y=x²﹣3x+m，直线l：y=kx（k＞0），当k=1时，抛物线C与直线l只有一个公共点．

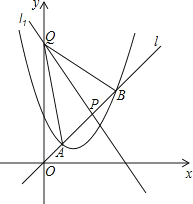(1)、求m的值；

(2)、若直线l与抛物线C交于不同的两点A，B，直线l与直线l₁：y=﹣3x+b交于点P，且

\frac{1}{O A}

+

\frac{1}{O B}

=

\frac{2}{O P}

，求b的值；

(3)、在（2）的条件下，设直线l₁与y轴交于点Q，问：是否在实数k使S_△_APQ=S_△_BPQ？若存在，求k的值，若不存在，说明理由．

查看试题解析

4.

如图，抛物线y=ax²+bx﹣3（a≠0）的顶点为E，该抛物线与x轴交于A、B两点，与y轴交于点C，且BO=OC=3AO，直线y=﹣ $\frac{1}{3}$ x+1与y轴交于点D．

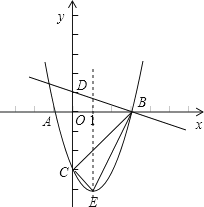(1)、求抛物线的解析式；

(2)、证明：△DBO∽△EBC；

(3)、在抛物线的对称轴上是否存在点P，使△PBC是等腰三角形？若存在，请直接写出符合条件的P点坐标，若不存在，请说明理由．

查看试题解析

5.

如图，抛物线y=ax²+2x﹣3与x轴交于A、B两点，且B（1，0）

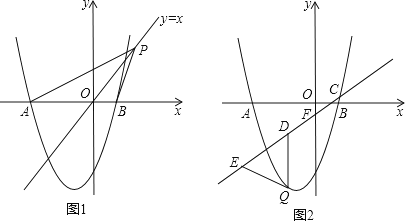(1)、求抛物线的解析式和点A的坐标；

(2)、如图1，点P是直线y=x上的动点，当直线y=x平分∠APB时，求点P的坐标；

(3)、如图2，已知直线y=

\frac{2}{3}

x﹣

\frac{4}{9}

分别与x轴、y轴交于C、F两点，点Q是直线CF下方的抛物线上的一个动点，过点Q作y轴的平行线，交直线CF于点D，点E在线段CD的延长线上，连接QE．问：以QD为腰的等腰△QDE的面积是否存在最大值？若存在，请求出这个最大值；若不存在，请说明理由．

查看试题解析

6.

如图，已知抛物线经过原点O，顶点为A（1，1），且与直线y=x﹣2交于B，C两点．

(1)、求抛物线的解析式及点C的坐标；

(2)、求证：△ABC是直角三角形；

(3)、若点N为x轴上的一个动点，过点N作MN⊥x轴与抛物线交于点M，则是否存在以O，M，N为顶点的三角形与△ABC相似？若存在，请求出点N的坐标；若不存在，请说明理由．

查看试题解析

7.

已知如图，在平面直角坐标系xOy中，点A、B、C分别为坐标轴上上的三个点，且OA=1，OB=3，OC=4，

(1)、求经过A、B、C三点的抛物线的解析式；

(2)、在平面直角坐标系xOy中是否存在一点P，使得以以点A、B、C、P为顶点的四边形为菱形？若存在，请求出点P的坐标；若不存在，请说明理由；

(3)、若点M为该抛物线上一动点，在（2）的条件下，请求出当|PM﹣AM|的最大值时点M的坐标，并直接写出|PM﹣AM|的最大值．

查看试题解析

8.

如图，已知抛物线y= $\frac{1}{3}$ x²+bx+c经过△ABC的三个顶点，其中点A（0，1），点B（﹣9，10），AC∥x轴，点P是直线AC下方抛物线上的动点．

(1)、求抛物线的解析式；

(2)、过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F，当四边形AECP的面积最大时，求点P的坐标；

(3)、当点P为抛物线的顶点时，在直线AC上是否存在点Q，使得以C、P、Q为顶点的三角形与△ABC相似，若存在，求出点Q的坐标，若不存在，请说明理由．

查看试题解析

9.

在矩形ABCD中，AB=3，AD=4，动点Q从点A出发，以每秒1个单位的速度，沿AB向点B移动；同时点P从点B出发，仍以每秒1个单位的速度，沿BC向点C移动，连接QP，QD，PD．若两个点同时运动的时间为x秒（0＜x≤3），解答下列问题：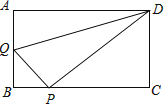

(1)、设△QPD的面积为S，用含x的函数关系式表示S；当x为何值时，S有最大值？并求出最小值；

(2)、是否存在x的值，使得QP⊥DP？试说明理由．

查看试题解析

10.

如图，在平面直角坐标系中，点O为坐标原点，直线l与抛物线y=mx²+nx相交于A（1，3 $\sqrt{3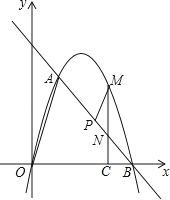}$ ），B（4，0）两点．

(1)、求出抛物线的解析式；

(2)、在坐标轴上是否存在点D，使得△ABD是以线段AB为斜边的直角三角形？若存在，求出点D的坐标；若不存在，说明理由；

(3)、点P是线段AB上一动点，（点P不与点A、B重合），过点P作PM∥OA，交第一象限内的抛物线于点M，过点M作MC⊥x轴于点C，交AB于点N，若△BCN、△PMN的面积S_△_BCN、S_△_PMN满足S_△_BCN=2S_△_PMN ，求出

\frac{M N}{N C}

的值，并求出此时点M的坐标．

查看试题解析

11.

如图，抛物线y=x²+bx+c与x轴交于A、B两点，B点坐标为（3，0），与y轴交于点C（0，﹣3）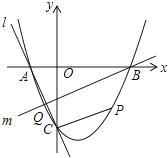

(1)、求抛物线的解析式；

(2)、点P在抛物线位于第四象限的部分上运动，当四边形ABPC的面积最大时，求点P的坐标和四边形ABPC的最大面积．

(3)、直线l经过A、C两点，点Q在抛物线位于y轴左侧的部分上运动，直线m经过点B和点Q，是否存在直线m，使得直线l、m与x轴围成的三角形和直线l、m与y轴围成的三角形相似？若存在，求出直线m的解析式，若不存在，请说明理由．

查看试题解析

12.

已知抛物线与x轴交于A（6，0）、B（﹣ $\frac{5}{4}$ ，0）两点，与y轴交于点C，过抛物线上点M（1，3）作MN⊥x轴于点N，连接OM．

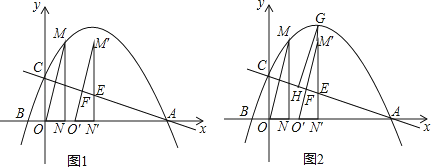(1)、求此抛物线的解析式；

(2)、如图1，将△OMN沿x轴向右平移t个单位（0≤t≤5）到△O′M′N′的位置，MN′、M′O′与直线AC分别交于点E、F．

①当点F为M′O′的中点时，求t的值；

②如图2，若直线M′N′与抛物线相交于点G，过点G作GH∥M′O′交AC于点H，试确定线段EH是否存在最大值？若存在，求出它的最大值及此时t的值；若不存在，请说明理由．

查看试题解析

13.

如图，在平面直角坐标系中，已知抛物线y=x²+bx+c过A，B，C三点，点A的坐标是（3，0），点C的坐标是（0，﹣3），动点P在抛物线上．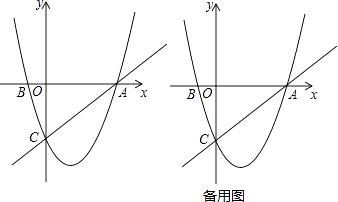

(1)、b= ， c= ，点B的坐标为；（直接填写结果）

(2)、是否存在点P，使得△ACP是以AC为直角边的直角三角形？若存在，求出所有符合条件的点P的坐标；若不存在，说明理由；

(3)、过动点P作PE垂直y轴于点E，交直线AC于点D，过点D作x轴的垂线．垂足为F，连接EF，当线段EF的长度最短时，求出点P的坐标．

查看试题解析

14.

如图1，对称轴为直线x= $\frac{1}{2}$ 的抛物线经过B（2，0）、C（0，4）两点，抛物线与x轴的另一交点为A

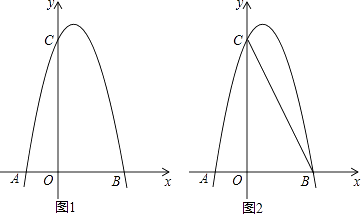(1)、求抛物线的解析式；

(2)、若点P为第一象限内抛物线上的一点，设四边形COBP的面积为S，求S的最大值；

(3)、如图2，若M是线段BC上一动点，在x轴是否存在这样的点Q，使△MQC为等腰三角形且△MQB为直角三角形？若存在，求出点Q的坐标；若不存在，请说明理由．

查看试题解析

15.

如图，抛物线y=ax²+bx﹣5（a≠0）与x轴交于点A（﹣5，0）和点B（3，0），与y轴交于点C．

(1)、求该抛物线的解析式；

(2)、若点E为x轴下方抛物线上的一动点，当S_△_ABE=S_△_ABC时，求点E的坐标；

(3)、在（2）的条件下，抛物线上是否存在点P，使∠BAP=∠CAE？若存在，求出点P的横坐标；若不存在，请说明理由．

查看试题解析

16. 已知Rt△ABC中，∠B=90°，AC=20，AB=10，P是边AC上一点（不包括端点A、C），过点P作PE⊥BC于点E，过点E作EF∥AC，交AB于点F．设PC=x，

PE=y．

(1)、求y与x的函数关系式；

(2)、是否存在点P使△PEF是Rt△？若存在，求此时的x的值；若不存在，请说明理由．

查看试题解析

17.

如图1，在直角坐标系xOy中，直线l：y=kx+b交x轴，y轴于点E，F，点B的坐标是（2，2），过点B分别作x轴、y轴的垂线，垂足为A、C，点D是线段CO上的动点，以BD为对称轴，作与△BCD或轴对称的△BC′D．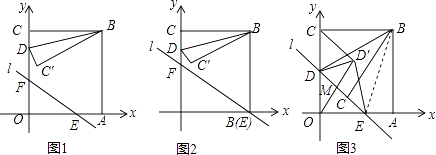

(1)、当∠CBD=15°时，求点C′的坐标．

(2)、当图1中的直线l经过点A，且k=﹣

\frac{\sqrt{3}}{3}

时（如图2），求点D由C到O的运动过程中，线段BC′扫过的图形与△OAF重叠部分的面积．

(3)、当图1中的直线l经过点D，C′时（如图3），以DE为对称轴，作于△DOE或轴对称的△DO′E，连结O′C，O′O，问是否存在点D，使得△DO′E与△CO′O相似？若存在，求出k、b的值；若不存在，请说明理由．

查看试题解析

18.

在线段AB的同侧作射线AM和BN，若∠MAB与∠NBA的平分线分别交射线BN，AM于点E，F，AE和BF交于点P．如图，点点同学发现当射线AM，BN交于点C；且∠ACB=60°时，有以下两个结论：

①∠APB=120°；②AF+BE=AB．

那么，当AM∥BN时：

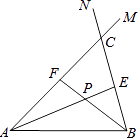(1)、点点发现的结论还成立吗？若成立，请给予证明；若不成立，请求出∠APB的度数，写出AF，BE，AB长度之间的等量关系，并给予证明；

(2)、设点Q为线段AE上一点，QB=5，若AF+BE=16，四边形ABEF的面积为32

\sqrt{3}

，求AQ的长．

查看试题解析

19.

如图，抛物线y=ax²+bx﹣4（a≠0）与x轴交于A（4，0）、B（﹣1，0）两点，过点A的直线y=﹣x+4交抛物线于点C．

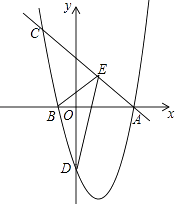(1)、求此抛物线的解析式；

(2)、在直线AC上有一动点E，当点E在某个位置时，使△BDE的周长最小，求此时E点坐标；

(3)、当动点E在直线AC与抛物线围成的封闭线A→C→B→D→A上运动时，是否存在使△BDE为直角三角形的情况，若存在，请直接写出符合要求的E点的坐标；若不存在，请说明理由．

查看试题解析

20.

如图，抛物线L：y=ax²+bx+c与x轴交于A、B（3，0）两点（A在B的左侧），与y轴交于点C（0，3），已知对称轴x=1．

(1)、求抛物线L的解析式；

(2)、将抛物线L向下平移h个单位长度，使平移后所得抛物线的顶点落在△OBC内（包括△OBC的边界），求h的取值范围；

(3)、设点P是抛物线L上任一点，点Q在直线l：x=﹣3上，△PBQ能否成为以点P为直角顶点的等腰直角三角形？若能，求出符合条件的点P的坐标；若不能，请说明理由．

查看试题解析

21.

如图，在平面直角坐标系中，抛物线y=ax²+2ax+c交x轴于A，B两点，交y轴于点C（0，3），tan∠OAC= $\frac{3}{4}$ ．

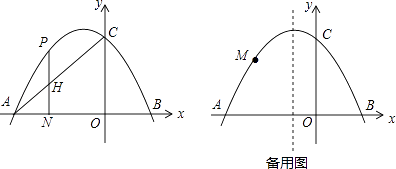(1)、求抛物线的解析式；

(2)、点H是线段AC上任意一点，过H作直线HN⊥x轴于点N，交抛物线于点P，求线段PH的最大值；

(3)、点M是抛物线上任意一点，连接CM，以CM为边作正方形CMEF，是否存在点M使点E恰好落在对称轴上？若存在，请求出点M的坐标；若不存在，请说明理由．

查看试题解析

中考备考专题复习：存在性问题

一、综合题