中考备考专题复习:阅读理解问题
试卷更新日期:2017-02-08 类型:二轮复习
一、单选题
-
1. 对于实数a,b,我们定义符号max{a,b}的意义为:当a≥b时,max{a,b}=a;当a<b时,max{a,b]=b,如:max{4,﹣2}=4,max{3,3}=3,若关于x的函数为y=max{x+3,﹣x+1},则该函数的最小值是( )
A、0 B、2 C、3 D、42. 对于实数a、b,定义一种新运算“⊗”为:a⊗b= ,这里等式右边是实数运算.例如:1⊗3= .则方程x⊗(﹣2)= ﹣1的解是( )A、x=4 B、x=5 C、x=6 D、x=73. 设a,b是实数,定义@的一种运算如下:a@b=(a+b)2﹣(a﹣b)2 , 则下列结论:①若a@b=0,则a=0或b=0
②a@(b+c)=a@b+a@c
③不存在实数a,b,满足a@b=a2+5b2
④设a,b是矩形的长和宽,若矩形的周长固定,则当a=b时,a@b最大.
其中正确的是( )
A、②③④ B、①③④ C、①②④ D、①②③4. 定义:点A(x,y)为平面直角坐标系内的点,若满足x=y,则把点A叫做“平衡点”.例如:M(1,1),N(﹣2,﹣2)都是“平衡点”.当﹣1≤x≤3时,直线y=2x+m上有“平衡点”,则m的取值范围是( )A、0≤m≤1 B、﹣3≤m≤1 C、﹣3≤m≤3 D、﹣1≤m≤0二、填空题
-
5. 阅读材料并解决问题:
求1+2+22+23+…+22014的值,令S=1+2+22+23+…+22014
等式两边同时乘以2,则2S=2+22+23+…+22014+22015
两式相减:得2S﹣S=22015﹣1
所以,S=22015﹣1
依据以上计算方法,计算1+3+32+33+…+32015= .
三、解答题
-
6. 自学下面材料后,解答问题.
分母中含有未知数的不等式叫分式不等式.如:等.那么如何求出它们的解集呢?
根据我们学过的有理数除法法则可知:两数相除,同号得正,异号得负.其字母表达式为:
(1)若a>0,b>0,则>0;若a<0,b<0,则>0;
(2)若a>0,b<0,则<0;若a<0,b>0,则<0.
反之:(1)若>0,则或
(2)<0,则____________ .
根据上述规律,求不等式>0的解集.
7. 阅读与计算:请阅读以下材料,并完成相应的任务.斐波那契(约1170﹣1250)是意大利数学家,他研究了一列数,这列数非常奇妙,被称为斐波那契数列(按照一定顺序排列着的一列数称为数列).后来人们在研究它的过程中,发现了许多意想不到的结果,在实际生活中,很多花朵(如梅花、飞燕草、万寿菊等)的瓣数恰是斐波那契数列中的数.斐波那契数列还有很多有趣的性质,在实际生活中也有广泛的应用.
斐波那契数列中的第n个数可以用[()n﹣()n]表示(其中,n≥1).这是用无理数表示有理数的一个范例.
任务:请根据以上材料,通过计算求出斐波那契数列中的第1个数和第2个数.
 8. 先阅读下列材料,然后解答问题:
8. 先阅读下列材料,然后解答问题:
材料1 从3张不同的卡片中选取2张排成一列,有6种不同的排法,抽象成数学问题就是从3个不同元素中选取2个元素的排列,排列数记为A32=3×2=6.
一般地,从n个不同元素中选取m个元素的排列数记作Anm ,
Anm=n(n-1)(n-2)…(n-m+1)(m≤n).
例:从5个不同元素中选3个元素排成一列的排列数为:A53=5×4×3=60.
材料2 从3张不同的卡片中选取2张,有3种不同的选法,抽象成数学问题就是从3个元素中选取2个元素的组合,组合数记为C32==3.
一般地,从n个不同元素中选取m个元素的组合数记作Cnm ,
Cnm= (m≤n).
例:从6个不同元素中选3个元素的组合数为:
C63==20.
问:(1)从7个人中选取4人排成一排,有多少种不同的排法?
(2)从某个学习小组8人中选取3人参加活动,有多少种不同的选法?
9. 定义新运算:对于任意实数m、n都有m☆n=m2n+n,等式右边是常用的加法、减法、乘法及乘方运算.例如:﹣3☆2=(﹣3)2×2+2=20.根据以上知识解决问题:若2☆a的值小于0,请判断方程:2x2﹣bx+a=0的根的情况.四、综合题
-
10. 阅读材料:
在一个三角形中,各边和它所对角的正弦的比相等,== , 利用上述结论可以求解如下题目:
在△ABC中,∠A、∠B、∠C的对边分别为a,b,c.若∠A=45°,∠B=30°,a=6,求b.
解:在△ABC中,∵=∴b====3 .
理解应用:
如图,甲船以每小时30海里的速度向正北方向航行,当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,且乙船从B1处按北偏东15°方向匀速直线航行,当甲船航行20分钟到达A2时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距10海里.
 (1)、判断△A1A2B2的形状,并给出证明(2)、求乙船每小时航行多少海里?11. 阅读下列材料:
(1)、判断△A1A2B2的形状,并给出证明(2)、求乙船每小时航行多少海里?11. 阅读下列材料:2015年清明小长假,北京市属公园开展以“清明踏青,春色满园”为主题的游园活动,虽然气温小幅走低,但游客踏青赏花的热情很高,市属公园游客接待量约为190万人次.其中,玉渊潭公园的樱花、北京植物园的桃花受到了游客的热捧,两公园的游客接待量分别为38万人次、21.75万人次;颐和园、天坛公园、北海公园因皇家园林的厚重文化底蕴与满园春色成为游客的重要目的地,游客接待量分别为26万人次、20万人次、17.6万人次;北京动物园游客接待量为18万人次,熊猫馆的游客密集度较高.
2014年清明小长假,天气晴好,北京市属公园游客接待量约为200万人次,其中,玉渊潭公园游客接待量比2013 年清明小长假增长了25%;颐和园游客接待量为26.2万人次,2013 年清明小长假增加了4.6万人次;北京动物园游客接待量为22万人次.
2013年清明小长假,玉渊潭公园、陶然亭公园、北京动物园游客接待量分别为32万人次、13万人次、14.9 万人次.
根据以上材料解答下列问题:
(1)、2014年清明小长假,玉渊潭公园游客接待量为 万人次(2)、选择统计表或统计图,将2013﹣2015年清明小长假玉渊潭公园、颐和园和北京动物园的游客接待量表示出来.12. 阅读下列材料,并用相关的思想方法解决问题.计算:(1﹣﹣﹣)×(+++)﹣(1﹣﹣﹣﹣)×(++).
令++=t,则
原式=(1﹣t)(t+)﹣(1﹣t﹣)t
=t+﹣t2﹣t﹣t+t2
=
问题:
(1)、计算(1﹣﹣﹣﹣…﹣)×(++++…++)﹣(1﹣﹣﹣﹣﹣…﹣﹣)×(+++…+);
(2)、解方程(x2+5x+1)(x2+5x+7)=7.13. 阅读下列材料,并解决相关的问题.按照一定顺序排列着的一列数称为数列,排在第一位的数称为第1项,记为a1 , 依此类推,排在第n位的数称为第n项,记为an .
一般地,如果一个数列从第二项起,每一项与它前一项的比等于同一个常数,那么这个数列叫做等比数列,这个常数叫做等比数列的公比,公比通常用字母q表示(q≠0).如:数列1,3,9,27,…为等比数列,其中a1=1,公比为q=3.
(1)、等比数列3,6,12,…的公比q为 ,第4项是(2)、如果一个数列a1 , a2 , a3 , a4 , …是等比数列,且公比为q,那么根据定义可得到:=q,=q,=q,…=q.所以:a2=a1•q,a3=a2•q=(a1•q)•q=a1•q2 , a4=a3•q=(a1•q2)•q=a1•q3 , …
由此可得:an=(用a1和q的代数式表示).
(3)、若一等比数列的公比q=2,第2项是10,请求它的第1项与第4项.14. 阅读材料:善于思考的小军在解方程组时,采用了一种“整体代换”的解法:解:将方程②变形:4x+10y+y=5 即2(2x+5y)+y=5③
把方程①代入③得:2×3+y=5,∴y=﹣1
把y=﹣1代入①得x=4,∴方程组的解为 .
请你解决以下问题:
(1)、模仿小军的“整体代换”法解方程组;(2)、已知x,y满足方程组(i)求x2+4y2的值;
(ii)求+的值.
15. 阅读理解材料一:一组对边平行,另一组对边不平行的四边形叫梯形,其中平行的两边叫梯形的底边,不平行的两边叫梯形的腰,连接梯形两腰中点的线段叫梯形的中位线.梯形的中位线具有以下性质:
梯形的中位线平行于两底,并且等于两底和的一半.
如图(1):在梯形ABCD中:AD∥BC
∵E、F是AB、CD的中点
∴EF∥AD∥BC
EF= (AD+BC)
材料二:经过三角形一边的中点与另一边平行的直线必平分第三边
如图(2):在△ABC中:
∵E是AB的中点,EF∥BC
∴F是AC的中点
如图(3)在梯形ABCD中,AD∥BC,AC⊥BD于O,E、F分别为AB、CD的中点,∠DBC=30°

请你运用所学知识,结合上述材料,解答下列问题.
(1)、求证:EF=AC;(2)、若OD= , OC=5,求MN的长.
16. 我们给出如下定义:顺次连接任意一个四边形各边中点所得的四边形叫中点四边形.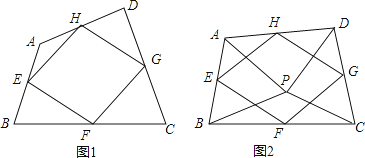 (1)、如图1,四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点.
(1)、如图1,四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点.求证:中点四边形EFGH是平行四边形;
(2)、如图2,点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想中点四边形EFGH的形状,并证明你的猜想;(3)、若改变(2)中的条件,使∠APB=∠CPD=90°,其他条件不变,直接写出中点四边形EFGH的形状.(不必证明)17. 已知点P(x0 , y0)和直线y=kx+b,则点P到直线y=kx+b的距离证明可用公式d= 计算.例如:求点P(﹣1,2)到直线y=3x+7的距离.
解:因为直线y=3x+7,其中k=3,b=7.
所以点P(﹣1,2)到直线y=3x+7的距离为:d= = = = .
根据以上材料,解答下列问题:
(1)、求点P(1,﹣1)到直线y=x﹣1的距离;(2)、已知⊙Q的圆心Q坐标为(0,5),半径r为2,判断⊙Q与直线y= x+9的位置关系并说明理由;(3)、已知直线y=﹣2x+4与y=﹣2x﹣6平行,求这两条直线之间的距离.18. 定义:有三个内角相等的四边形叫三等角四边形.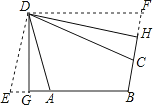 (1)、三等角四边形ABCD中,∠A=∠B=∠C,求∠A的取值范围;(2)、如图,折叠平行四边形纸片DEBF,使顶点E,F分别落在边BE,BF上的点A,C处,折痕分别为DG,DH.求证:四边形ABCD是三等角四边形.(3)、三等角四边形ABCD中,∠A=∠B=∠C,若CB=CD=4,则当AD的长为何值时,AB的长最大,其最大值是多少?并求此时对角线AC的长.19. 我们定义:有一组邻角相等的凸四边形叫做“等邻角四边形”
(1)、三等角四边形ABCD中,∠A=∠B=∠C,求∠A的取值范围;(2)、如图,折叠平行四边形纸片DEBF,使顶点E,F分别落在边BE,BF上的点A,C处,折痕分别为DG,DH.求证:四边形ABCD是三等角四边形.(3)、三等角四边形ABCD中,∠A=∠B=∠C,若CB=CD=4,则当AD的长为何值时,AB的长最大,其最大值是多少?并求此时对角线AC的长.19. 我们定义:有一组邻角相等的凸四边形叫做“等邻角四边形” (1)、概念理解:
(1)、概念理解:请你根据上述定义举一个等邻角四边形的例子;
(2)、问题探究;如图1,在等邻角四边形ABCD中,∠DAB=∠ABC,AD,BC的中垂线恰好交于AB边上一点P,连结AC,BD,试探究AC与BD的数量关系,并说明理由;
(3)、应用拓展;如图2,在Rt△ABC与Rt△ABD中,∠C=∠D=90°,BC=BD=3,AB=5,将Rt△ABD绕着点A顺时针旋转角α(0°<∠α<∠BAC)得到Rt△AB′D′(如图3),当凸四边形AD′BC为等邻角四边形时,求出它的面积.
20. 阅读下列材料:北京市正围绕着“政治中心、文化中心、国际交往中心、科技创新中心”的定位,深入实施“人文北京、科技北京、绿色北京”的发展战略.“十二五”期间,北京市文化创意产业展现了良好的发展基础和巨大的发展潜力,已经成为首都经济增长的支柱产业.
2011年,北京市文化创意产业实现增加值1938.6亿元,占地区生产总值的12.2%.2012年,北京市文化创意产业继续呈现平稳发展态势,实现产业增加值2189.2亿元,占地区生产总值的12.3%,是第三产业中仅次于金融业、批发和零售业的第三大支柱产业.2013年,北京市文化产业实现增加值2406.7亿元,比上年增长9.1%,文化创意产业作为北京市支柱产业已经排到了第二位.2014年,北京市文化创意产业实现增加值2749.3亿元,占地区生产总值的13.1%,创历史新高,2015年,北京市文化创意产业发展总体平稳,实现产业增加值3072.3亿元,占地区生产总值的13.4%.
根据以上材料解答下列问题:
(1)、用折线图将2011﹣2015年北京市文化创意产业实现增加值表示出来,并在图中标明相应数据;(2)、根据绘制的折线图中提供的信息,预估2016年北京市文化创意产业实现增加值约亿元,你的预估理由 .21. 阅读材料:关于三角函数还有如下的公式:sin(α±β)=sinαcosβ±cosαsinβ
tan(α±β)=
利用这些公式可以将一些不是特殊角的三角函数转化为特殊角的三角函数来求值.
例:tan75°=tan(45°+30°)= = =2+
根据以上阅读材料,请选择适当的公式解答下面问题
 (1)、计算:sin15°;(2)、某校在开展爱国主义教育活动中,来到烈士纪念碑前缅怀和纪念为国捐躯的红军战士.李三同学想用所学知识来测量如图纪念碑的高度.已知李三站在离纪念碑底7米的C处,在D点测得纪念碑碑顶的仰角为75°,DC为 米,请你帮助李三求出纪念碑的高度.22. 阅读下面材料:
(1)、计算:sin15°;(2)、某校在开展爱国主义教育活动中,来到烈士纪念碑前缅怀和纪念为国捐躯的红军战士.李三同学想用所学知识来测量如图纪念碑的高度.已知李三站在离纪念碑底7米的C处,在D点测得纪念碑碑顶的仰角为75°,DC为 米,请你帮助李三求出纪念碑的高度.22. 阅读下面材料:小明遇到这样一个问题:如图1,△ABC中,AB=AC,点D在BC边上,∠DAB=∠ABD,BE⊥AD,垂足为E,求证:BC=2AE.
小明经探究发现,过点A作AF⊥BC,垂足为F,得到∠AFB=∠BEA,从而可证△ABF≌△BAE(如图2),使问题得到解决.
 (1)、根据阅读材料回答:△ABF与△BAE全等的条件是 AAS(填“SSS”、“SAS”、“ASA”、“AAS”或“HL”中的一个)
(1)、根据阅读材料回答:△ABF与△BAE全等的条件是 AAS(填“SSS”、“SAS”、“ASA”、“AAS”或“HL”中的一个)参考小明思考问题的方法,解答下列问题:
(2)、如图3,△ABC中,AB=AC,∠BAC=90°,D为BC的中点,E为DC的中点,点F在AC的延长线上,且∠CDF=∠EAC,若CF=2,求AB的长;(3)、如图4,△ABC中,AB=AC,∠BAC=120°,点D、E分别在AB、AC边上,且AD=kDB(其中0<k< ),∠AED=∠BCD,求 的值(用含k的式子表示).
-