中考备考专题复习：方案设计问题
试卷更新日期：2017-02-08 类型：二轮复习
一、单选题
-
1. 宜宾市某化工厂，现有A种原料52千克，B种原料64千克，现用这些原料生产甲、乙两种产品共20件．已知生产1件甲种产品需要A种原料3千克，B种原料2千克；生产1件乙种产品需要A种原料2千克，B种原料4千克，则生产方案的种数为（ ）A、4 B、5 C、6 D、72. 为了丰富学生课外小组活动，培养学生动手操作能力，王老师让学生把5m长的彩绳截成2m或1m的彩绳，用来做手工编织，在不造成浪费的前提下，你有几种不同的截法（ ）A、1 B、2 C、3 D、43. 表为小洁打算在某电信公司购买一支MAT手机与搭配一个门号的两种方案．此公司每个月收取通话费与月租费的方式如下：若通话费超过月租费，只收通话费；若通话费不超过月租费，只收月租费．若小洁每个月的通话费均为x元，x为400到600之间的整数，则在不考虑其他费用并使用两年的情况下，x至少为多少才会使得选择乙方案的总花费比甲方案便宜？（ ）
甲方案
乙方案
门号的月租费（元）
400
600
MAT手机价格（元）
15000
13000
注意事项：以上方案两年内不可变更月租费
A、500 B、516 C、517 D、6004. 8月份是新学期开学准备季，东风和百惠两书店对学习用品和工具实施优惠销售．优惠方案分别是：在东风书店购买学习用品或工具书累计花费60元后，超出部分按50%收费；在百惠书店购买学习用品或工具书累计花费50元后，超出部分按60%收费，郝爱同学准备买价值300元的学习用品和工具书，她在哪家书店消费更优惠（ ）A、东风 B、百惠 C、两家一样 D、不能确定二、解答题
-
5. 随着私家车拥有量的增加，停车问题已经给人们的生活带来了很多不便．为了缓解停车矛盾，某小区开发商欲投资16万元，建造若干个停车位，考虑到实际因素，计划露天车位的数量不少于室内车位的2倍，但不超过室内车位的3倍．据测算，建造费用及年租金如下表：
类别
室内车位
露天车位
建造费用（元/个）
5 000
1 000
年租金（元/个）
2 000
800
（1）该开发商有哪几种符合题意的建造方案？写出解答过程．
（2）若按表中的价格将两种车位全部出租，哪种方案获得的年租金最多？并求出此种方案的年租金．（不考虑其他费用）
三、综合题
-
6. 某学校是乒乓球体育传统项目学校，为进一步推动该项目的开展，学校准备到体育用品店购买直拍球拍和横拍球拍若干副，并且每买一副球拍必须要买10个乒乓球，乒乓球的单价为2元/个，若购买20副直拍球拍和15副横拍球拍花费9000元；购买10副横拍球拍比购买5副直拍球拍多花费1600元．(1)、求两种球拍每副各多少元？(2)、若学校购买两种球拍共40副，且直拍球拍的数量不多于横拍球拍数量的3倍，请你给出一种费用最少的方案，并求出该方案所需费用．7. 为保障我国海外维和部队官兵的生活，现需通过A港口、B港口分别运送100吨和50吨生活物资．已知该物资在甲仓库存有80吨，乙仓库存有70吨，若从甲、乙两仓库运送物资到港口的费用（元/吨）如表所示：
港口
运费（元/台）
甲库
乙库
A港
14
20
B港
10
8
(1)、设从甲仓库运送到A港口的物资为x吨，求总运费y（元）与x（吨）之间的函数关系式，并写出x的取值范围；(2)、求出最低费用，并说明费用最低时的调配方案．8. 某商店购进甲乙两种商品，甲的进货单价比乙的进货单价高20元，已知20个甲商品的进货总价与25个乙商品的进货总价相同．(1)、求甲、乙每个商品的进货单价；(2)、若甲、乙两种商品共进货100件，要求两种商品的进货总价不高于9000元，同时甲商品按进价提高10%后的价格销售，乙商品按进价提高25%后的价格销售，两种商品全部售完后的销售总额不低于10480元，问有哪几种进货方案？(3)、在条件（2）下，并且不再考虑其他因素，若甲乙两种商品全部售完，哪种方案利润最大？最大利润是多少？9. 现代互联网技术的广泛应用，催生了快递行业的高速发展．小明计划给朋友快递一部分物品，经了解有甲、乙两家快递公司比较合适．甲公司表示：快递物品不超过1千克的，按每千克22元收费；超过1千克，超过的部分按每千克15元收费．乙公司表示：按每千克16元收费，另加包装费3元．设小明快递物品x千克．(1)、请分别写出甲、乙两家快递公司快递该物品的费用y（元）与x（千克）之间的函数关系式；(2)、小明选择哪家快递公司更省钱？10. 荔枝是深圳的特色水果，小明的妈妈先购买了2千克桂味和3千克糯米糍，共花费90元；后又购买了1千克桂味和2千克糯米糍，共花费55元．（每次两种荔枝的售价都不变）(1)、求桂味和糯米糍的售价分别是每千克多少元；(2)、如果还需购买两种荔枝共12千克，要求糯米糍的数量不少于桂味数量的2倍，请设计一种购买方案，使所需总费用最低．11. 倡导健康生活，推进全民健身，某社区要购进A，B两种型号的健身器材若干套，A，B两种型号健身器材的购买单价分别为每套310元，460元，且每种型号健身器材必须整套购买．(1)、若购买A，B两种型号的健身器材共50套，且恰好支出20000元，求A，B两种型号健身器材各购买多少套？(2)、若购买A，B两种型号的健身器材共50套，且支出不超过18000元，求A种型号健身器材至少要购买多少套？12. 某中学开学初到商场购买A、B两种品牌的足球，购买A种品牌的足球50个，B种品牌的足球25个，共花费4500元，已知购买一个B种品牌的足球比购买一个A钟品牌的足球多花30元．(1)、求购买一个A种品牌、一个B种品牌的足球各需多少元．(2)、学校为了响应习总书记“足球进校园”的号召，决定再次购进A、B两种品牌足球共50个，正好赶上商场对商品价格进行调整，A品牌足球售价比第一次购买时提高4元，B品牌足球按第一次购买时售价的9折出售，如果学校此次购买A、B两种品牌足球的总费用不超过第一次花费的70%，且保证这次购买的B种品牌足球不少于23个，则这次学校有哪几种购买方案？(3)、请你求出学校在第二次购买活动中最多需要多少资金？13. （列方程（组）及不等式解应用题）春节期间，某商场计划购进甲、乙两种商品，已知购进甲商品2件和乙商品3件共需270元；购进甲商品3件和乙商品2件共需230元．
(1)、求甲、乙两种商品每件的进价分别是多少元？(2)、商场决定甲商品以每件40元出售，乙商品以每件90元出售，为满足市场需求，需购进甲、乙两种商品共100件，且甲种商品的数量不少于乙种商品数量的4倍，请你求出获利最大的进货方案，并确定最大利润．14. 公司有330台机器需要一次性运送到某地，计划租用甲、乙两种货车共8辆，已知每辆甲种货车一次最多运送机器45台、租车费用为400元，每辆乙种货车一次最多运送机器30台、租车费用为280元(1)、设租用甲种货车x辆（x为非负整数），试填写表格．表一：
租用甲种货车的数量/辆
3
7
x
租用的甲种货车最多运送机器的数量/台
135
租用的乙种货车最多运送机器的数量/台
150
表二：
租用甲种货车的数量/辆
3
7
x
租用甲种货车的费用/元
2800
租用乙种货车的费用/元
280
(2)、给出能完成此项运送任务的最节省费用的租车方案，并说明理由．15. 为了提高身体素质，有些人选择到专业的健身中心锻炼身体，某健身中心的消费方式如下：普通消费：35元/次；
白金卡消费：购卡280元/张，凭卡免费消费10次再送2次；
钻石卡消费：购卡560元/张，凭卡每次消费不再收费．
以上消费卡使用年限均为一年，每位顾客只能购买一张卡，且只限本人使用．
(1)、李叔叔每年去该健身中心健身6次，他应选择哪种消费方式更合算？(2)、设一年内去该健身中心健身x次（x为正整数），所需总费用为y元，请分别写出选择普通消费和白金卡消费的y与x的函数关系式；(3)、王阿姨每年去该健身中心健身至少18次，请通过计算帮助王阿姨选择最合算的消费方式．16. 我州某养殖场计划购买甲、乙两种鱼苗600条，甲种鱼苗每条16元，乙种鱼苗每条20元，相关资料表明：甲、乙两种鱼苗的成活率为80%，90%(1)、若购买这两种鱼苗共用去11000元，则甲、乙两种鱼苗各购买多少条？(2)、若要使这批鱼苗的总成活率不低于85%，则乙种鱼苗至少购买多少条？(3)、在（2）的条件下，应如何选购鱼苗，使购买鱼苗的总费用最低？最低费用是多少？17. 小丽购买学习用品的收据如表，因污损导致部分数据无法识别，根据下表，解决下列问题：(1)、小丽买了自动铅笔、记号笔各几支？(2)、若小丽再次购买软皮笔记本和自动铅笔两种文具，共花费15元，则有哪几种不同的购买方案？商品名
单价（元）
数量（个）
金额（元）
签字笔
3
2
6
自动铅笔
1.5
●
●
记号笔
4
●
●
软皮笔记本
●
2
9
圆规
3.5
1
●
合计
8
28
18. 随着信息技术的快速发展，“互联网+”渗透到我们日常生活的各个领域，网上在线学习交流已不再是梦，现有某教学网站策划了A，B两种上网学习的月收费方式：收费方式
月使用费/元
包时上网时间/h
超时费/（元/min）
A
7
25
0.01
B
m
n
0.01
设每月上网学习时间为x小时，方案A，B的收费金额分别为yA ， yB ．
(1)、如图是yB与x之间函数关系的图象，请根据图象填空：m= n=
(2)、写出与x之间的函数关系式．(3)、选择哪种方式上网学习合算，为什么？19. 在学习概率的课堂上，老师提出问题：只有一张电影票，小明和小刚想通过抽取扑克牌的游戏来决定谁去看电影，请你设计一个对小明和小刚都公平的方案．甲同学的方案：将红桃2、3、4、5四张牌背面向上，小明先抽一张，小刚从剩下的三张牌中抽一张，若两张牌上的数字之和是奇数，则小明看电影，否则小刚看电影．
(1)、甲同学的方案公平吗？请用列表或画树状图的方法说明；(2)、乙同学将甲的方案修改为只用红桃2、3、4三张牌，抽取方式及规则不变，乙的方案公平吗？（只回答，不说明理由）20. 新农村社区改造中，有一部分楼盘要对外销售，某楼盘共23层，销售价格如下：第八层楼房售价为4000元/米2 ， 从第八层起每上升一层，每平方米的售价提高50元；反之，楼层每下降一层，每平方米的售价降低30元，已知该楼盘每套楼房面积均为120米2 ．若购买者一次性付清所有房款，开发商有两种优惠方案：
方案一：降价8%，另外每套楼房赠送a元装修基金；
方案二：降价10%，没有其他赠送．
(1)、请写出售价y（元/米2）与楼层x（1≤x≤23，x取整数）之间的函数关系式；
(2)、老王要购买第十六层的一套楼房，若他一次性付清购房款，请帮他计算哪种优惠方案更加合算.
21. 某足球协会举办了一次足球联赛，其记分规定及奖励方案如下表：胜一场
平一场
负一场
积分
3
1
0
奖金（元/人）
1300
500
0
当比赛进行到第11轮结束（每队均须比赛11场）时，A队共积17分，每赛一场，每名参赛队员均得出场费300元．设A队其中一名参赛队员所得的奖金与出场费的和为w（元）．
(1)、试说明w是否能等于11400元．(2)、通过计算，判断A队胜、平、负各几场，并说明w可能的最大值.22.甲、乙两家草莓采摘园的草莓品质相同，销售价格也相同．“五一期间”，两家均推出了优惠方案，甲采摘园的优惠方案是：游客进园需购买50元的门票，采摘的草莓六折优惠；乙采摘园的优惠方案是：游客进园不需购买门票，采摘园的草莓超过一定数量后，超过部分打折优惠．优惠期间，设某游客的草莓采摘量为x（千克），在甲采摘园所需总费用为y1（元），在乙采摘园所需总费用为y2（元），图中折线OAB表示y2与x之间的函数关系．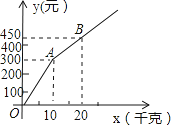
(1)、甲、乙两采摘园优惠前的草莓销售价格是每千克元；
(2)、求y1、y2与x的函数表达式；(3)、在图中画出y1与x的函数图象，并写出选择甲采摘园所需总费用较少时，草莓采摘量x的范围．23. 课本中有一个例题：有一个窗户形状如图1，上部是一个半圆，下部是一个矩形，如果制作窗框的材料总长为6m，如何设计这个窗户，使透光面积最大？
这个例题的答案是：当窗户半圆的半径约为0.35m时，透光面积最大值约为1.05m2 ．
我们如果改变这个窗户的形状，上部改为由两个正方形组成的矩形，如图2，材料总长仍为6m，利用图3，解答下列问题：
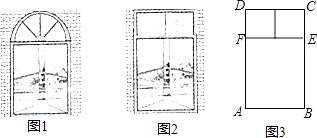(1)、若AB为1m，求此时窗户的透光面积？(2)、与课本中的例题比较，改变窗户形状后，窗户透光面积的最大值有没有变大？请通过计算说明．24. 某景点试开放期间，团队收费方案如下：不超过30人时，人均收费120元；超过30人且不超过m（30＜m≤100）人时，每增加1人，人均收费降低1元；超过m人时，人均收费都按照m人时的标准．设景点接待有x名游客的某团队，收取总费用为y元．(1)、求y关于x的函数表达式；(2)、景点工作人员发现：当接待某团队人数超过一定数量时，会出现随着人数的增加收取的总费用反而减少这一现象．为了让收取的总费用随着团队中人数的增加而增加，求m的取值范围．
-